乘积最大子数组

news2025/1/12 1:34:52

题目链接

乘积最大子数组

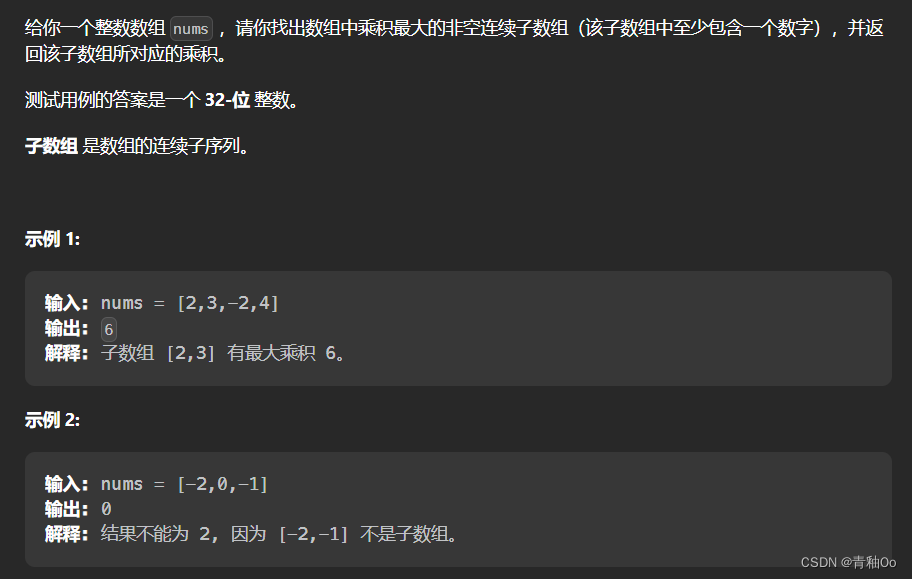
题目描述

注意点

-10 <= nums[i] <= 10
nums 的任何前缀或后缀的乘积都保证是一个 32-位整数

解答思路

最初想到求和最大的子数组所用的贪心算法，判断包括该元素时的最大值tmp，再将当前最大值res与tmp比较，全部遍历完就可找到和最大的子数组
本题由于是乘积可能由正数变为负数，由负数变为正数，所以使用动态规划的思想，遍历整个数组，求出包括任意i位置元素时的乘积最大正数和乘积最大负数，在求i + 1位置处的最大正数和最大负数时，则根据i位置的最大正数和最大负数再乘i + 1位置的元素值再与i + 1位置的元素值进行比较，找出i + 1位置的最大整数和最大负数，遍历完整个数组即可找到乘积最大子数组

代码

class Solution {
    public int maxProduct(int[] nums) {
        int tmpMin = nums[0];
        int tmpMax = nums[0];
        int res = nums[0];
        for (int i = 1; i < nums.length; i++) {
            int preMin = tmpMin;
            int preMax = tmpMax;
            tmpMin = Math.min(nums[i], Math.min(nums[i] * preMax, nums[i] * preMin));
            tmpMax = Math.max(nums[i], Math.max(nums[i] * preMax, nums[i] * preMin));
            res = Math.max(res, tmpMax);
        }
        return res;
    }
}