算法随想录刷题60Day

---

目录

动态规划简介

动态规划简单应用

斐波那契

 爬楼梯

 使用最小开支爬楼

---

动态规划简介

动态规划(Dynamic Programming)是一种解决复杂问题的算法设计思想。它的主要思路是将原问题拆分若干个子问题，并分别求解这些子问题，最后将这些子问题组合优化得到原问题的解。

动态规划算法设计一般分为以下五个步骤(动规五部曲):

1. 确立动规数组的大小及其下标的含义。

2. 确定状态转移方程（递推公式）。

3. 初始化动规数组开始的几个元素(边界条件)。

4. 确定动规数组的遍历方向或顺序。

5. 举例测试该动规数组是否可行。

动态规划的关键在于找到合适的状态定义和状态转移方程。通过将大问题划分为小问题，并利用子问题的解来求解大问题，动态规划能够有效地降低问题的复杂度，避免重复计算，提高算法的效率。

动态规划简单应用

斐波那契

	int fib(int n) 
	{
		vector<int> dp(n + 1, 0);
		dp[0] = 0;
		if (n > 0)dp[1] = 1;
		for (int i = 2; i <= n; ++i)
			dp[i] = dp[i - 1] + dp[i - 2];
		return dp[n];
	}

 爬楼梯

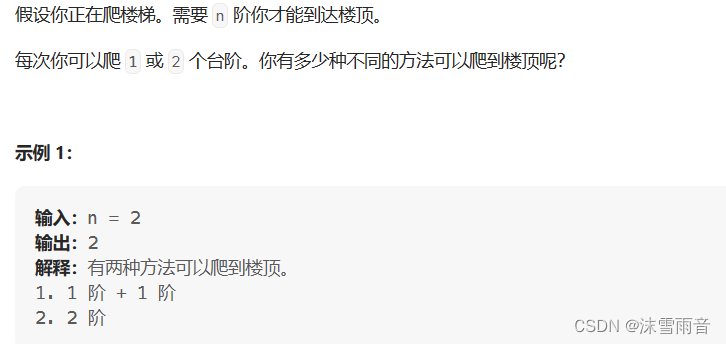
	int climbStairs(int n)
	{
		vector<int> dp(n + 1, 0);
		dp[1] = 1;
		if (n > 1)dp[2] = 2;
		for (int i = 2; i <= n; ++i)
			dp[i] = dp[i - 1] + dp[i - 2];
		return dp[n];
	}

 使用最小开支爬楼

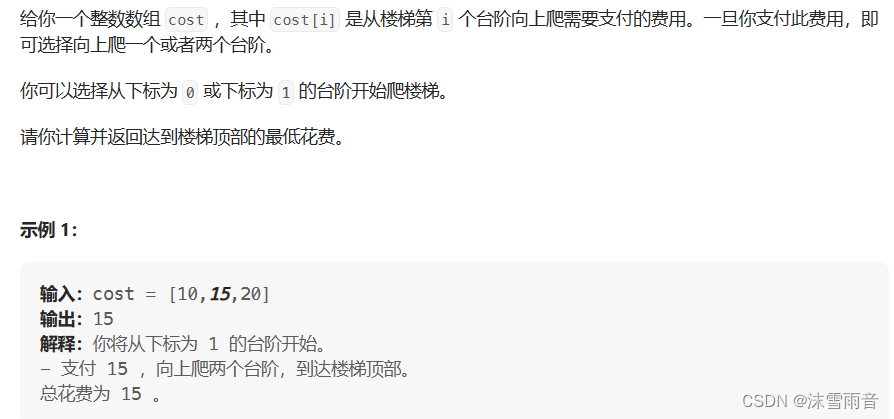
	int minCostClimbingStairs(vector<int>& cost)
	{
		int n = cost.size();
		vector<int> dp(n, 0);
		if (cost.size() == 2)return min(cost[0], cost[1]);
		for (int i = 2; i < n; ++i)
			dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
		return min(dp[n - 1] + cost[n - 1], dp[n - 2] + cost[n - 2]);
	}

---