DRCN: Deeply-Recursive Convolutional Network for Image Super-Resolution
总结
这篇文章是第一次将之前已有的递归神经网络(Recursive Neural Network)结构应用在图像超分辨率上。为了增加网络的感受野,提高网络性能,引入了深度递归神经网络,递归模块权重共享减少了模型所需参数量,但出现了梯度爆炸/消失问题,又研究出了递归监督和跳跃连接两个扩展办法。
特点:
- 递归监督:把每次递归后的特征映射都用于重建目标高分辨率图像HR。由于每次递归都会导致不同的HR预测,因此作者将不同级别的递归产生的所有预测结合起来,以提供更准确的最终预测。每次递归的预测都受到GT监督
- 跳跃连接:在SR中,低分辨率图像(输入)和高分辨率图像(输出)在很大程度上共享相同的信息。输入的精确信息在许多向前传递过程中可能会衰减。于是作者将输入和各层的输出连接到重建层,用于图像的恢复。缓解网络记忆负担,网络只需要学习残差
- 原始LR图像经过插值上采样后提升分辨率后再进入网络
方法细节
基础模型:
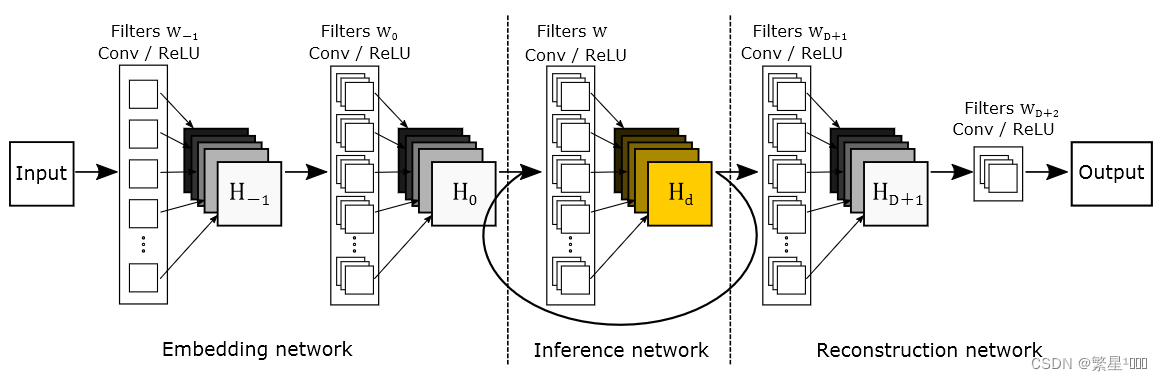
基底模型由三个子网络组成:嵌入网络embedding netword、推理网络 inference network 和 重建网络reconstruction network。
- 嵌入网络用于将给定图像表示为特征映射,
- 推理网络加深网络深度,将嵌入网络的输出特征映射到更高维度。注意推理网络是递归调用的。
- 重建网络根据推理网络中的最终特征映射生成输出图像。
- 上图中的input图像是原始LR图像经过插值上采样后的图像。
存在问题:
- 梯度的消失和爆炸。梯度爆炸是由链式梯度的乘法性质造成的。对于深度递归,可以呈指数增长。梯度消失问题正好与梯度爆炸相反。梯度呈指数级的速度到零向量。因此,梯度爆炸和消失的存在使深度递归网络掌握远距离像素信息间的关系非常困难。
- 经过多次递归想要保留原始LR信息并不容易。在SR任务中,输出与输入非常相似,所以LR图像的信息非常重要,需要为后续更深的递归层保留输入图像的精确信息。
- 存在一个寻找最优递归次数的问题。如果递归对于给定的任务来说太深,就需要减少递归的次数。寻找最优数需要训练许多具有不同递归深度的网络。
进阶模型
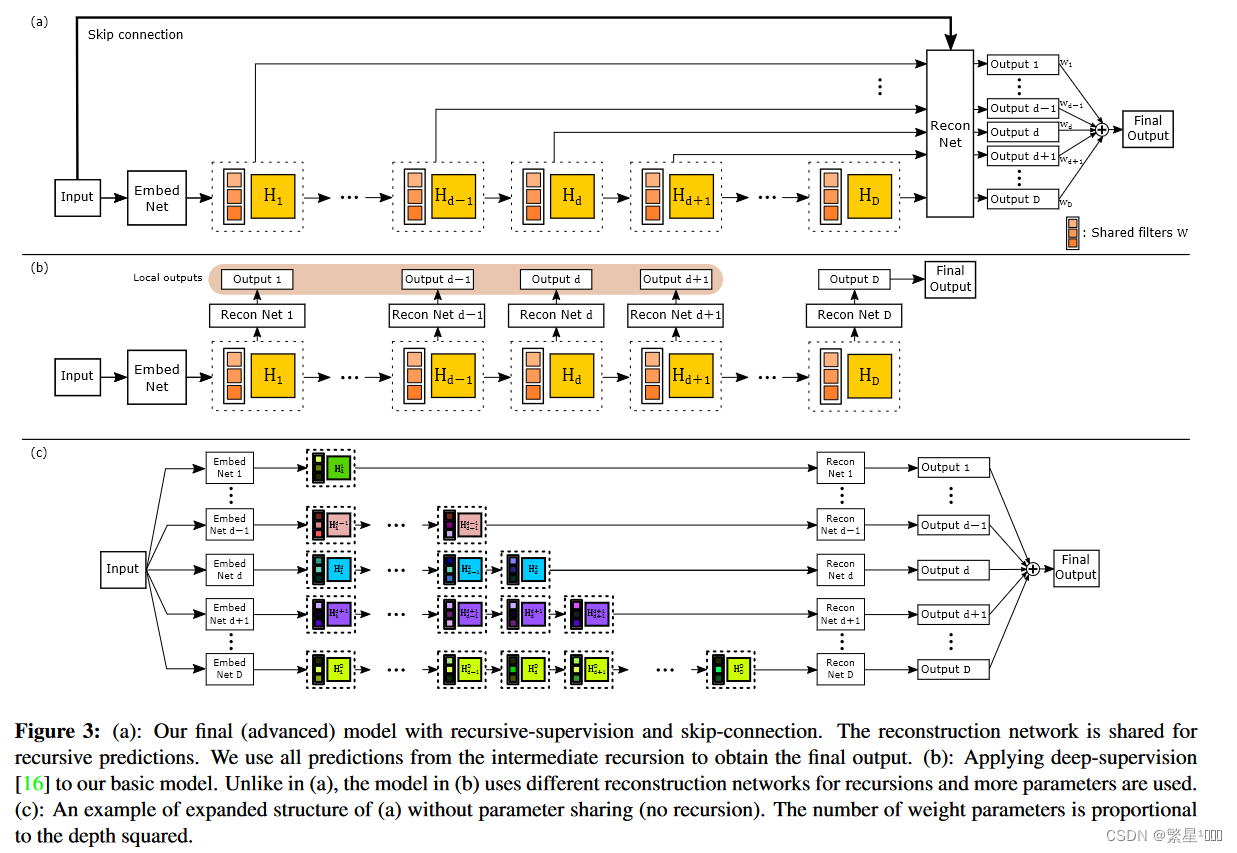
图a是文章最终的模型:
-
Recursive-Supervision:监督每层递归,以减轻梯度消失/爆炸的影响。假设在推理层中卷积过程反复使用相同的卷积核,使用相同的重建层来预测每一次递归重建的SR图像。重建层输出D个预测图像,所有预测都在训练期间同时受到监督,这一步在公式中的体现为增加了一部分loss,后面公式中具体再介绍。
a、将所有D个预测图像通过加权求和来计算最终输出(权重由网络学习得到)。通过递归轻了训练递归网络的困难,通过反向传播将不同预测损失产生的反传梯度求和提供平滑效果,能够有效缓解梯度爆炸或消失。
b、此外,由于监督能够利用所有中间层的预测信息,因此选择最佳递归次数的重要性降低了。 -
Skip-Connection:对于图像重建任务,输入和输出图像高度相关,所以可以直接通过跳层连接将LR信息直接传输到SR重建层。该做法有两个优点:节约了远距离传输的复杂算力、极大程度的保留了完整的低频信息。
参考文章
超分算法DRCN:Deeply-Recursive Convolutional Network for Image Super-Resolution超分辨率重建
DRRN: Image Super-Resolution via Deep Recursive Residual
总结
作者点明了在图像进入网络之前做插值处理的弊端(增加计算量),提到了在ESPCN超分辨网络中使用的Sub-Pixel策略,这种方法是通过在网络末端做分辨率提升,进而减小了计算量和缓解了网络的记忆负担。
引入全局和局部残差学习。类似于ResNet,引入了残差单元(这也意味着引入了局部残差学习),使得网络运行几层就会进行一次残差学习(这样更有利于网络运行过程中的高频信息重建和保持),同时在最后的输出层也会进行一次大的残差学习。
方法
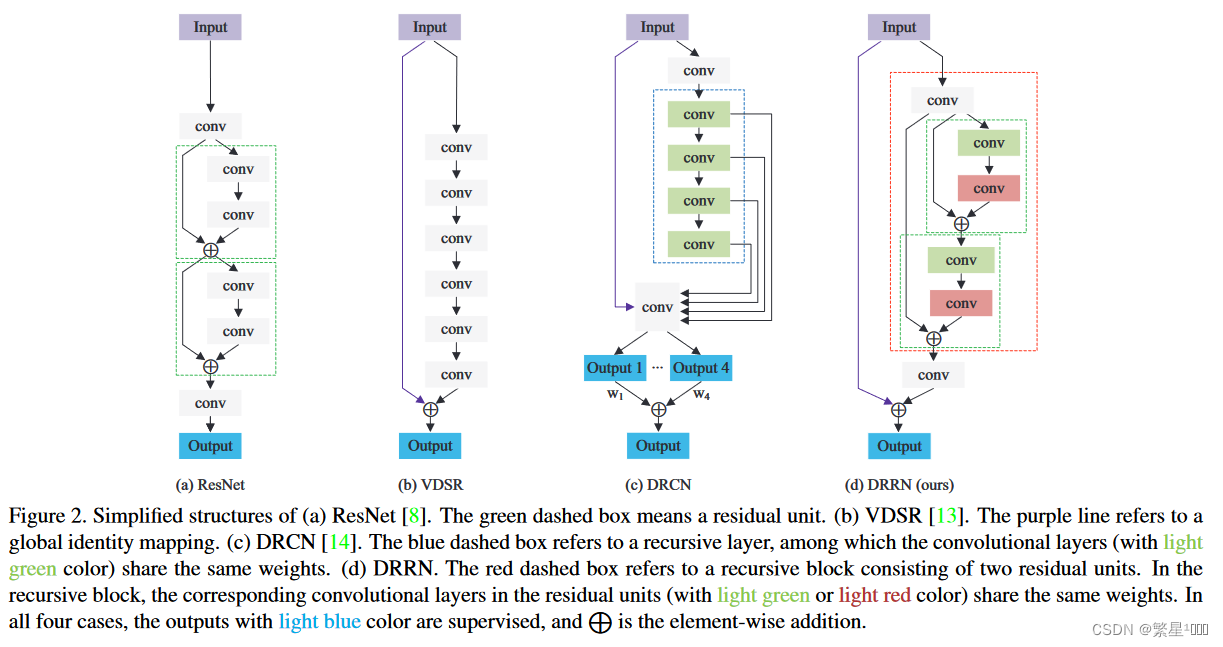

残差递归块
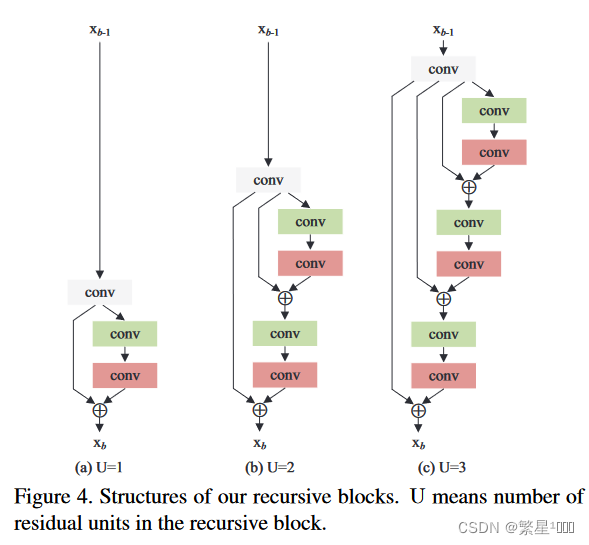
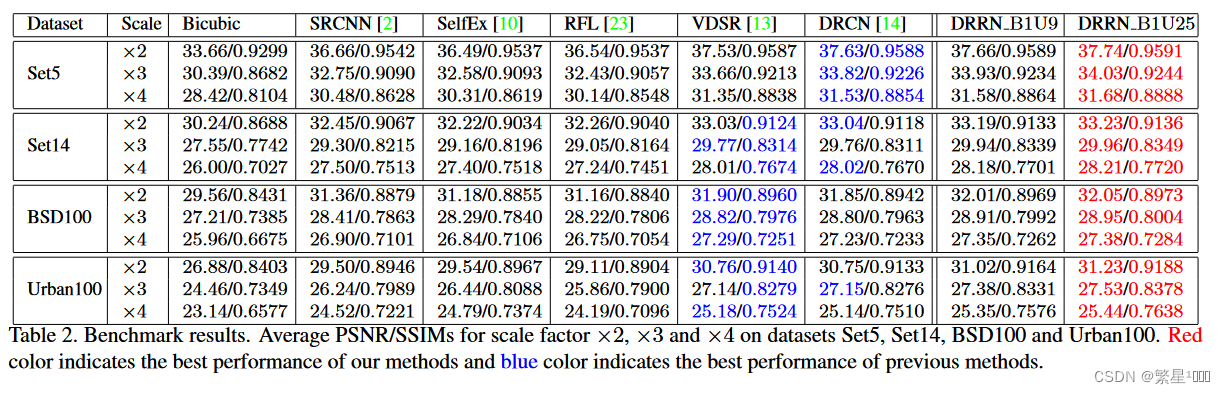
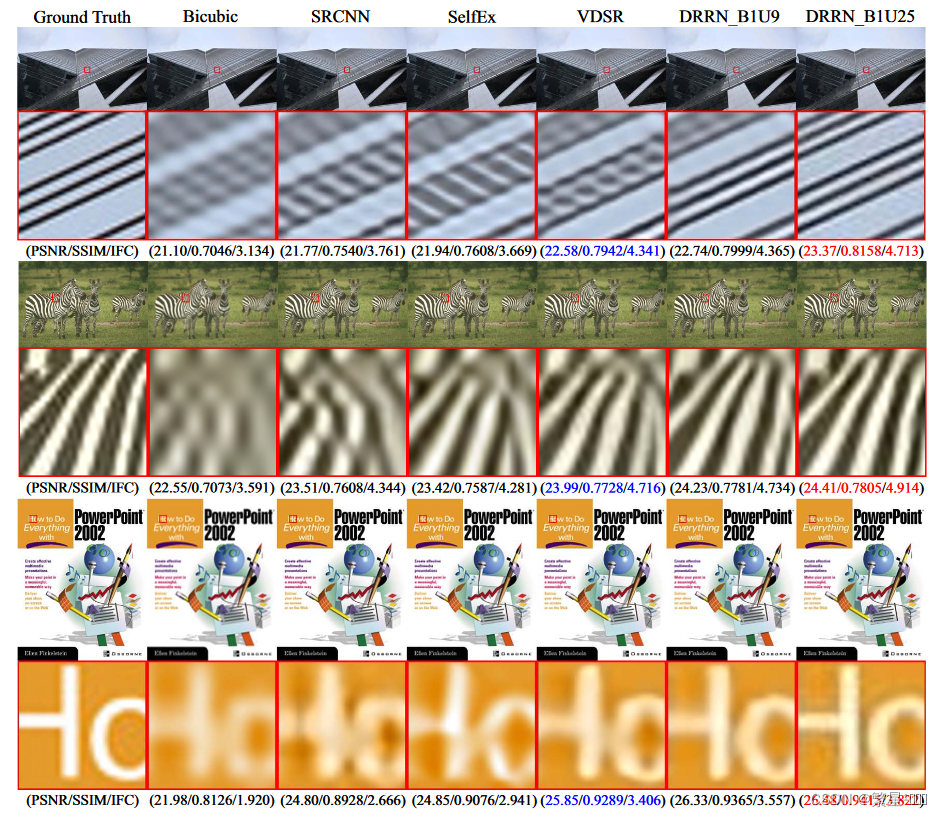
性能
LapSRN: Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution
总结
使用拉普拉斯金字塔结构的思想,逐步进行2的幂次的超分,并且结合残差来进行模型预测。
论文的创新点有:
- 准确性高。LapSRN使用Charbonnier loss来改善重建质量,可以减少artifacts.
- 速度快。与FSRCNN一样,可以在大多数的测试集上可以实时超分。
- 逐步重建。模型使用拉普拉斯金字塔的结构,在一次预测的过程中生成多张中间结果,可以作为不同倍数的超分结果。
之前方法的问题:
- 一些方法使用预定义好的上采样操作,来将低分辨率输入插值到高分辨率输出再来进行超分。这样会造成增加计算量和产生伪影(increases unnecessary computational cost and often results in visible reconstruction artifacts)。虽然有着FSRCNN使用反卷积和ESPCN使用亚像素卷积来对SRCNN类的方法进行加速,但是由于输入分辨率太高,约束着模型结构的容量,无法学习更为复杂的映射关系。
- L2 Loss对噪声敏感,文中说L2 loss产生的图像过于平滑,与人眼感知不符
- 多数方法仅用一个上采样获得最终的图片,对于8x很困难
- 现有的方法无法产生中间过程,需要针对具有不同期望上采样比例和计算负荷的各种应用来训练各种各样的模型
方法
方法异同对比
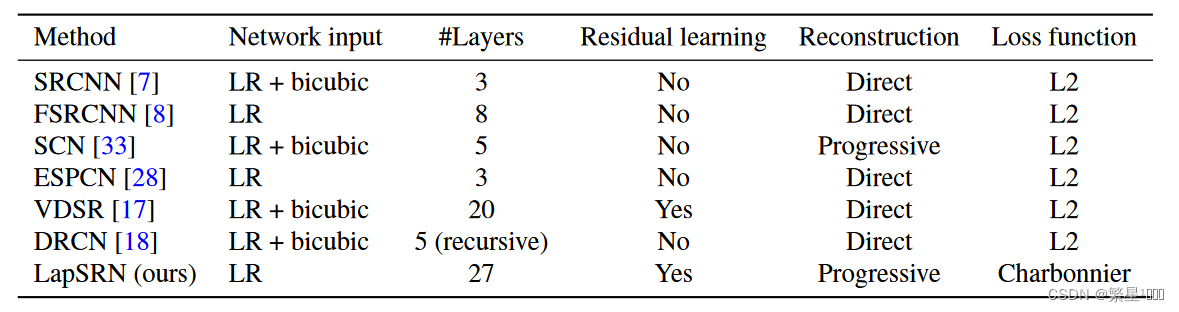
现有方法
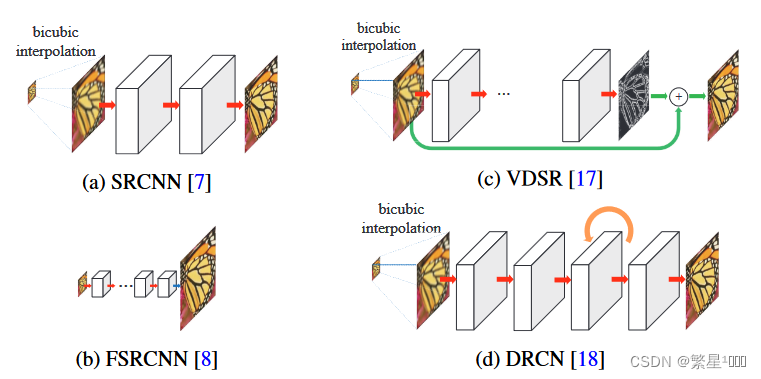
本文方法
- 绿色表示元素级的加操作,橙色表示递归卷积层,蓝色表示转置卷积
- 两个模块
- 特征提取:d层的卷积(提取[level s]分辨率l特征)+1层的反卷积(上采样到[level s+1]更精细分辨率的特征),然后再分两条支路:一条再通过卷积层重建残差图像,一条递归调用d层卷积继续提取[level s+1]分辨率l特征。由于前面d层卷积是在低分辨率上操作的,相比在输入网络前就将图像上采样到高分辨率的方法,运算量大幅减小。
- 上采样:scale为2的转置卷积(反卷积)上采样图像+残差图像,对应位置元素相加
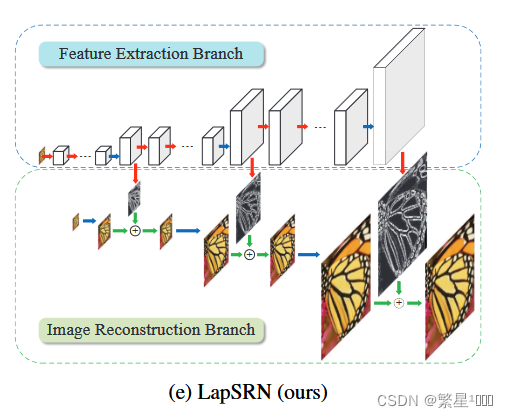
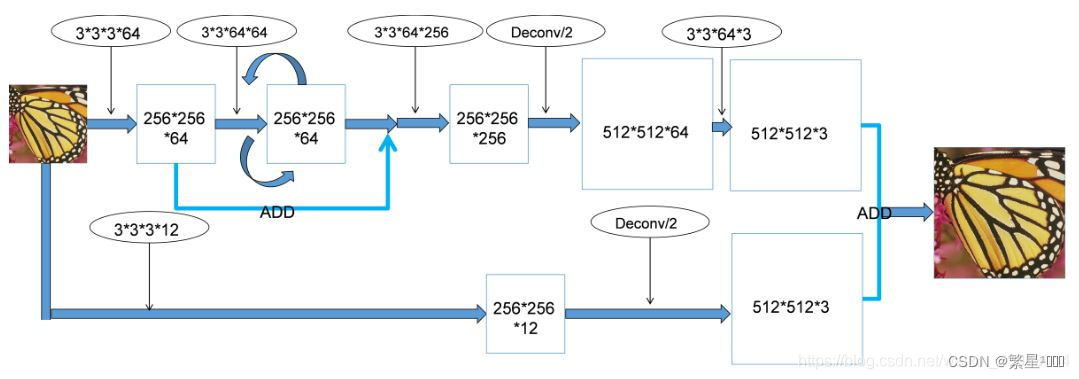
递归网络模型框架
loss: Charbonnier
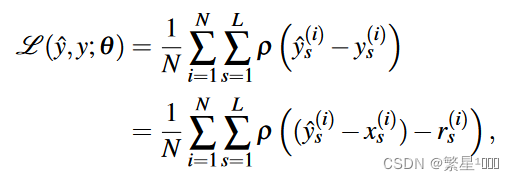
- y ^ s \hat{y}_s y^s是网络预测的level s的HR图像
- y s y_s ys是GT 的level s的HR图像,从原始高分辨图像通过双三次下采样得到
- x s x_s xs是低分辨率图像上采样的图像
- r s r_s rs是leve s的残差图像
文章中说理想的输出高分辨图像由这个公式建模,
y
s
=
x
s
+
r
s
y_s=x_s+r_s
ys=xs+rs.
其实我的理解,
x
s
x_s
xs和
r
s
r_s
rs都是网络预测的,应该是网络预测得到level s的HR图像
y
^
s
=
x
s
+
r
s
\hat{y}_s=x_s+r_s
y^s=xs+rs
所以loss应该写成:
ζ
(
y
^
,
y
;
θ
)
=
1
N
∑
i
=
1
N
∑
s
=
1
L
ρ
(
y
s
(
i
)
−
y
^
s
(
i
)
)
=
1
N
∑
i
=
1
N
∑
s
=
1
L
ρ
(
y
s
(
i
)
−
(
x
s
(
i
)
+
r
s
(
i
)
)
)
\zeta(\hat{y},y;\theta)=\frac{1}{N}\sum_{i=1}^{N}\sum_{s=1}^{L}\rho(y_s^{(i)}-\hat{y}_s^{(i)})=\frac{1}{N}\sum_{i=1}^{N}\sum_{s=1}^{L}\rho(y_s^{(i)}-(x_s^{(i)}+r_s^{(i)}))
ζ(y^,y;θ)=N1i=1∑Ns=1∑Lρ(ys(i)−y^s(i))=N1i=1∑Ns=1∑Lρ(ys(i)−(xs(i)+rs(i)))
ρ(x)=sqrt(x2+ϵ2)是Charbonnier penalty function(L1范数的变体),N是每个批次的数量,L是金字塔的级数。在这种损失函数下,金字塔每级的输出都会靠近某个尺度下的HR,因此才可以同时实现2x,4x,8x的超分辨。
Charbonnier loss(也称为L1-Charbonnier loss或Huber loss)是一种用于计算图像重建或图像生成任务中的损失函数。它是由Charbonnier在1989年提出的,用于解决图像处理中的平滑和噪声问题。
Charbonnier loss主要用于替代传统的L2损失(平方差损失),因为L2损失对于离群值(异常值)比较敏感,因为平方会放大误差,容易导致模型对于噪声或细节部分过度平滑化。相比之下,Charbonnier loss对于离群值的响应相对较小,能够更好地保留细节信息。
Charbonnier loss的计算公式如下:
L Charbonnier ( x , y ) = ( x − y ) 2 + ϵ 2 L_{\text{Charbonnier}}(x, y) = \sqrt{(x - y)^2 + \epsilon^2} LCharbonnier(x,y)=(x−y)2+ϵ2
其中, x x x是模型生成的输出, y y y是真实的目标值, ϵ \epsilon ϵ是一个小的正数(通常取较小的值,如 1 0 − 3 10^{-3} 10−3或 1 0 − 6 10^{-6} 10−6),用于避免除以零的情况。
Charbonnier loss计算了预测值和目标值之间的差异,并加上了一个平方项和一个平滑项,从而在保持平滑性的同时对异常值有一定的容忍度。通过最小化Charbonnier loss,模型可以更好地适应噪声、保留细节,并生成更加清晰和真实的图像。
需要注意的是,Charbonnier loss只是损失函数的一种选择,根据具体任务和需求,也可以选择其他类型的损失函数来优化模型。
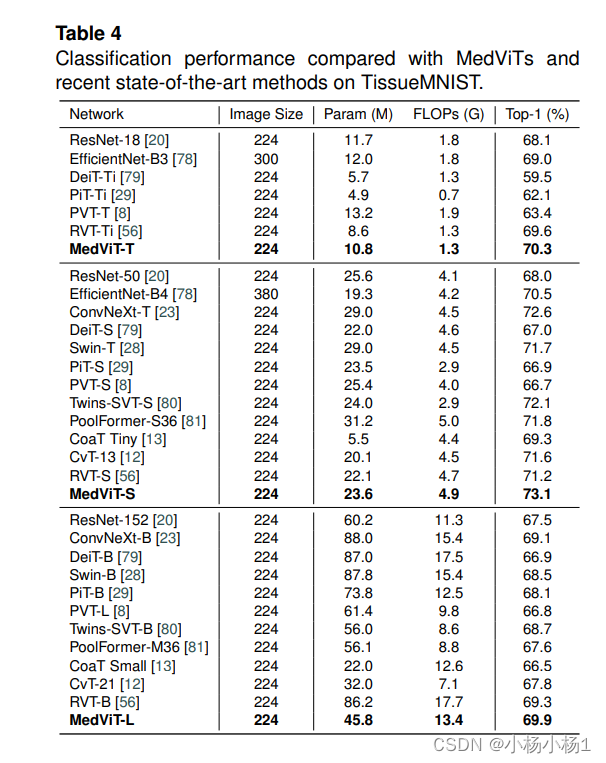
性能
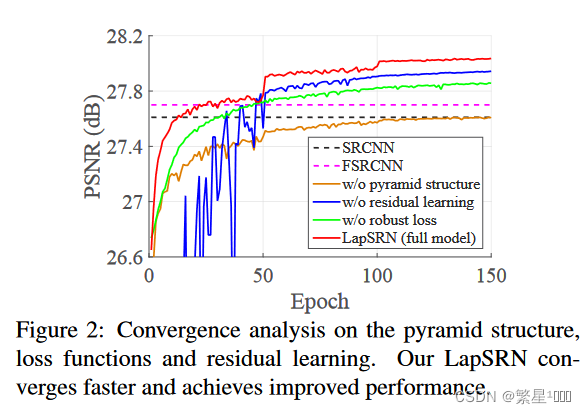
消融实验
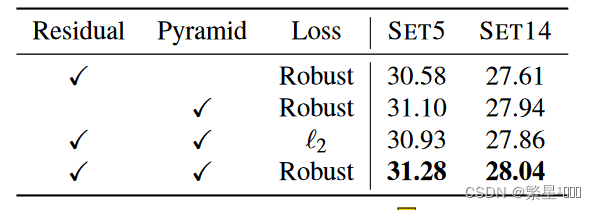
可以发现Pyramid 和 Robust loss对性能的影响更显著,残差虽然对性能的影响没有那么显著,但是可以使网络收敛更快,loss更不会抖动。
一个设计是否有用,不光可以比较性能,还可以看:复杂度,收敛速度,训练难度,loss抖动,额外收益等等。
参考文章
经典回顾:LapSRN
[超分][CVPR2017]LapSRN




![java八股文面试[数据结构]——Map有哪些子类](https://img-blog.csdnimg.cn/img_convert/f28213e65f48d3855f45b092bb0fee52.png)