2023-08-22每日一题

一、题目编号

849. 到最近的人的最大距离

二、题目链接

点击跳转到题目位置

三、题目描述

给你一个数组 seats 表示一排座位，其中 seats[i] = 1 代表有人坐在第 i 个座位上，seats[i] = 0 代表座位 i 上是空的（下标从 0 开始）。

至少有一个空座位，且至少有一人已经坐在座位上。

亚历克斯希望坐在一个能够使他与离他最近的人之间的距离达到最大化的座位上。

返回他到离他最近的人的最大距离。

示例 1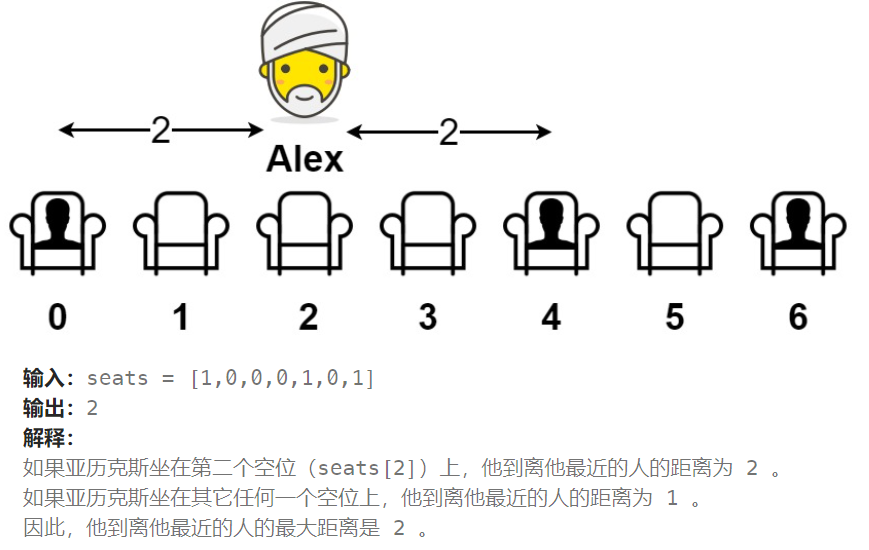： 在这里插入图片描述
示例2：

示例3：

提示：

2 <= seats.length <= 2 * 10⁴
seats[i] 为 0 或 1
至少有一个空座位
至少有一个座位上有人

四、解题代码

class Solution {
public:
    int maxDistToClosest(vector<int>& seats) {
        int dp1[20010];
        int dp2[20010];
        int max0 = 0;
        int n = seats.size();
        memset(dp1, 0, sizeof(dp1));
        memset(dp2, 0, sizeof(dp2));
        for(int i = 0; i < n; ++i){
            if(i == 0){
                if(seats[i]){
                    dp1[i] = 1;
                } else{
                    dp1[i] = 0;
                }
                continue;
            }
            if(seats[i]){
                dp1[i] = i + 1;
            } else{
                dp1[i] = dp1[i - 1];
            }
        }
        for(int i = n - 1; i >= 0; --i){
            if(seats[i]){
                dp2[i] = i + 1;
            } else{
                dp2[i] = dp2[i + 1];
            }
        }
        int len = 0;
        for(int i = 0; i < n; ++i){
            if(dp1[i] == i + 1 || dp2[i] == i + 1){
                continue;
            } else{
                int left = 0;
                int right = 0;
                if(dp1[i] == 0){
                    len = max(len, max(i + 1, dp2[i] - 1 - i));
                    continue;
                } else{
                    left = i + 1 - dp1[i];
                }
                if(dp2[i] == 0){
                    len = max(len, max(n - 1 - i, i + 1 - dp1[i]));
                    continue;
                } else{
                    right = dp2[i] - 1 - i;
                }
                len = max(len, min(left, right)); 
            }
        }
    return len;
    }
};