在写shader相关的程序的时候往往需要用到 OpenGL内置的数学库,下面列举几个常用的函数用法和效果,下面的所有代码都是运行在shadertoy在线工具上的,推荐一个好用的数学工具desmosDesmos
目录:
- abs(x)
- step(edge,x)
- dot(uv1,uv2)
1:abs(x) 取绝对值
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
// Normalized pixel coordinates (from 0 to 1)
vec2 uv = fragCoord/iResolution.xy;
uv -= 0.5;
uv.x *= iResolution.x / iResolution.y;
vec3 col = vec3(0.);
uv = abs(uv);
float c = uv.x;
// 0.2 <= c => 0 0.2 > c => 1 step(.2,c) reverse color
col += step(c,.2);
// Output to screen
fragColor = vec4(col,1.0);
}一般abs操作的时候会对uv坐标取绝对值,一般应用于对称的图形绘制上。
2:step(edge,x) 取0或者1: 函数通常用于比较输入值与阈值,并返回一个阶跃函数的结果。阶跃函数的意思是,如果输入值小于或等于阈值,则返回0;如果输入值大于阈值,则返回1。
col += c;
// 0.2 <= c => 0 0.2 > c => 1 step(.2,c) reverse color
col += step(c,.2);如果使用的是 step(0.2,c)那么如果c > 0.2 返回1,c <= 0.2 返回0,反应到图形是就是黑白块的显著分割
如果反过来 step(c,0.2) 的结果就是颠倒黑白显示,原理很好理解 如果0.2 > c 返回1,如果0.2 <= c返回0,也就是 c < 0.2 => 1 c >= 0.2 => 0 正好与上述的方法相反。

3: dot(a,b) 在着色器中,dot() 函数通常用于计算两个向量的点积。点积是将两个向量相乘并将结果相加得到的标量值。dot() 函数在着色器中经常用于计算光照模型中的光照强度,或者进行向量投影、判断两个向量的相关性等操作
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
// Normalized pixel coordinates (from 0 to 1)
vec2 uv = fragCoord/iResolution.xy;
uv -= 0.5;
uv.x *= iResolution.x / iResolution.y;
vec3 col = vec3(0.);
//uv = abs(uv);
// 根据uv坐标来决定哪些地方显示白色那些地方显示黑色 c只是控制颜色的显示,
// uv决定哪些地方显示那些颜色
float c = dot(uv,vec2(3.,1.));
col += c;
// 0.2 <= c => 0 0.2 > c => 1 step(.2,c) reverse color
//col += step(c,0.2);
// Output to screen
fragColor = vec4(col,1.0);
}可能单纯的dot函数你并不能看出来图形为什么这么显示,那么知道dot的数学公式之后你会豁然开朗的感觉 dot(a,b) = a.x * b.x + a.y * b.y
那么上面的dot(uv,vec2(3,1)) 表示的就是 c = uv.x * 3 + uv.y * 1 也就是 0 = 3x + y - c 怎么样这个公式熟悉不熟悉,这就是高中学到的曲线方程,再想到高中学到的曲线的动态规划 曲线的右上方的点都大于零,曲线上的点都等于零,曲线的左下方小于零,这样不是很直观我还是上图吧:
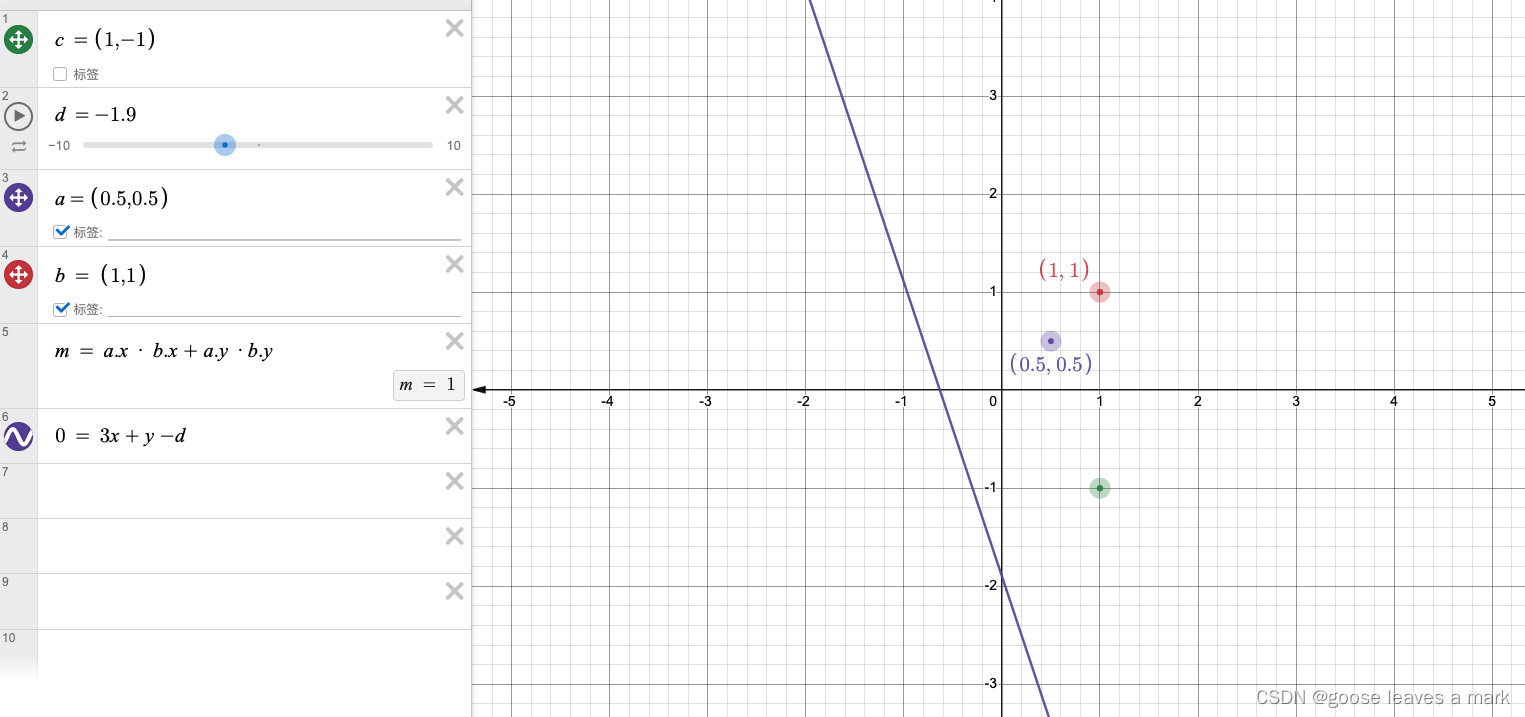
移动d滑块就会发现,d > 0的时候曲线是向右上方移动的,d<0的时候是向曲线的左下方移动的,所以图像显示成下图这样也就不奇怪了,这样你就知道了图形为啥这样显示了:

结合上面的abs方法,我们打开abs会发现,所得到的图形就是右上角的图像经过x轴y轴两次对折得到的结果


接着看step怎么控制图形的形状的 我们打开 col += step(0.2,c),可以看到 中间出现了菱形的黑色色块,为什么是黑色的并且 为什么跟上图的大小差别那么大,原因就是0.2控制了菱形显示的大小,只要是大于0.2的像素都会被step函数跃迁到1这个值,所以就得到如下的结果
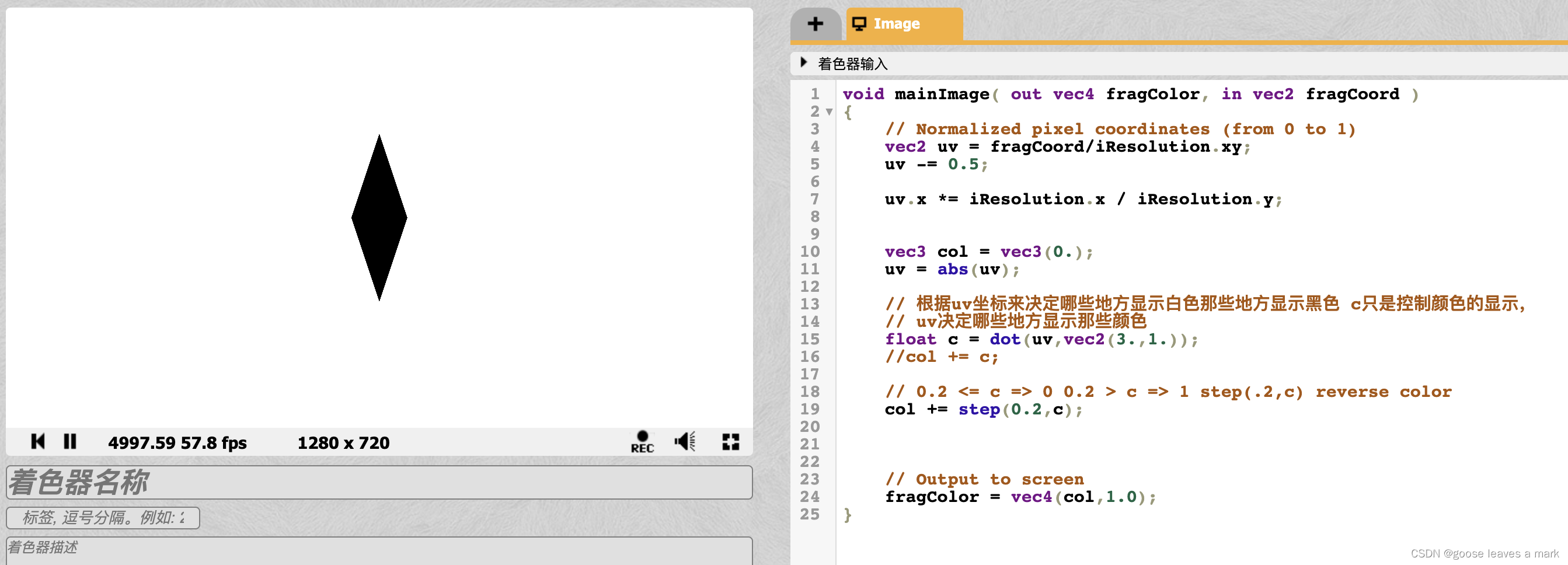
如果我们不想让中间的黑块显示成黑色的而是想让它显示白色的怎么办呢,那好办直接反转 step函数的两个参数就可以了 step(c,0.2)