前言

变分自编码器(Variational auto-encoder,VAE) 是以自编码器结构为基础的深度生成模型。自编码器在降维和特征提取等领域应用广泛, 基本结构是通过编码 (Encoder) 过程将样本映射到低维空间的隐变量, 然后通过解码 (Decoder) 过程将隐变量还原为重构样本。

一、AE（auto-encoders）-自编码器

自编码器是一种数据维度压缩算法，通常用于构建一种能够输入样本并进行特征表达的神经网络和可以通过训练多层神经网络样本得到参数初始值。

1.AE整体结构及公式推导

图中的输入数据$x$与对应的连接权重$W$相乘，再加上偏置$b$,经过激活函数$f(\cdot )$变换后，得到y。具体公式如下：
$$y=f(Wx+b)$$
自编码器是一种基于无监督学习的神经网络，目的在于通过不断调整参数，重构经过维度压缩的输入样本。输入层到中间层之间的映射称为编码，把中间层到输出层之间的映射称为解码。自编码器通常先通过编码得到压缩后向量，再通过解码进行重构。

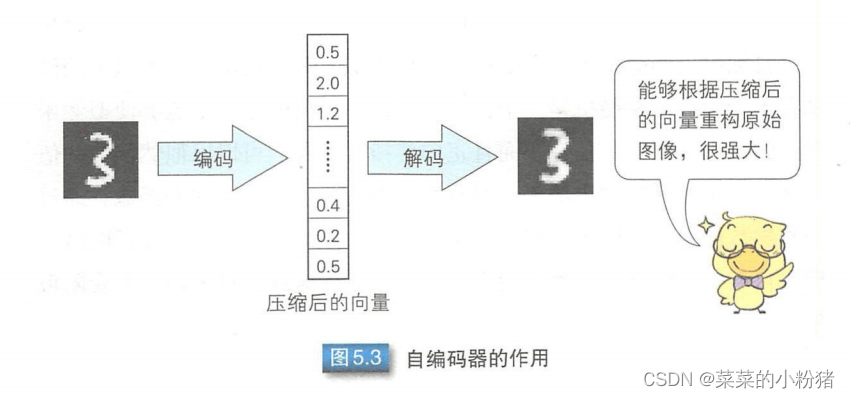
注：图来自于《图解深度学习》

中间层和重构层之间的连接权重及偏置分为记作$\tilde{W}$和$\tilde{b}$，重构结果记作$\tilde{x}$。
$$\tilde{x}=\tilde{f}(\tilde{W}y+\tilde{b})$$
这里的$\tilde{f}(\cdot )$表示解码器的激活函数。
重构层的$\tilde{x}$可以表示为：
$$\tilde{x}=\tilde{f}(\tilde{W}f(Wx+b)+\tilde{b})$$
误差函数（$Loss$函数）$E$可以使用最小二乘法差函数或者交叉熵代价函数。
$$\begin{gathered} E=\sum _{n=1}^N\Vert x_n-\widetilde{x_n}{\Vert }^2 \\ E=-\sum _{n=1}^N(x_{i}log{\tilde{x}}_i+(1-x_i)log(1-{\tilde{x}}_i)) \end{gathered}$$
上面公式中的$x_i$和${\tilde{x}}_i$分别代表$x$和$\tilde{x}$的第$i$个元素。

2.AE的特点

AE包含以下特点：

• 非监督学习 (Unsupervised Learning)
• 是一种前馈神经网络，没有任何反馈
• 是一种生成模型
• 具有较好的特征提取能力
• 它的降维可以是非线性的，而 PCA 是线性的
• 常用于 特征提取、文档检索、分类和异常检测

二、 VAE(Variational auto-encoder)-变分自编码器

VAE模型的基本结构与自编码相似，两者区别在于VAE中的隐藏变量$z$是随机变量、构造的似然函数的变分下界和重参数化编码器输出的均值和方差。

1.VAE模型结构

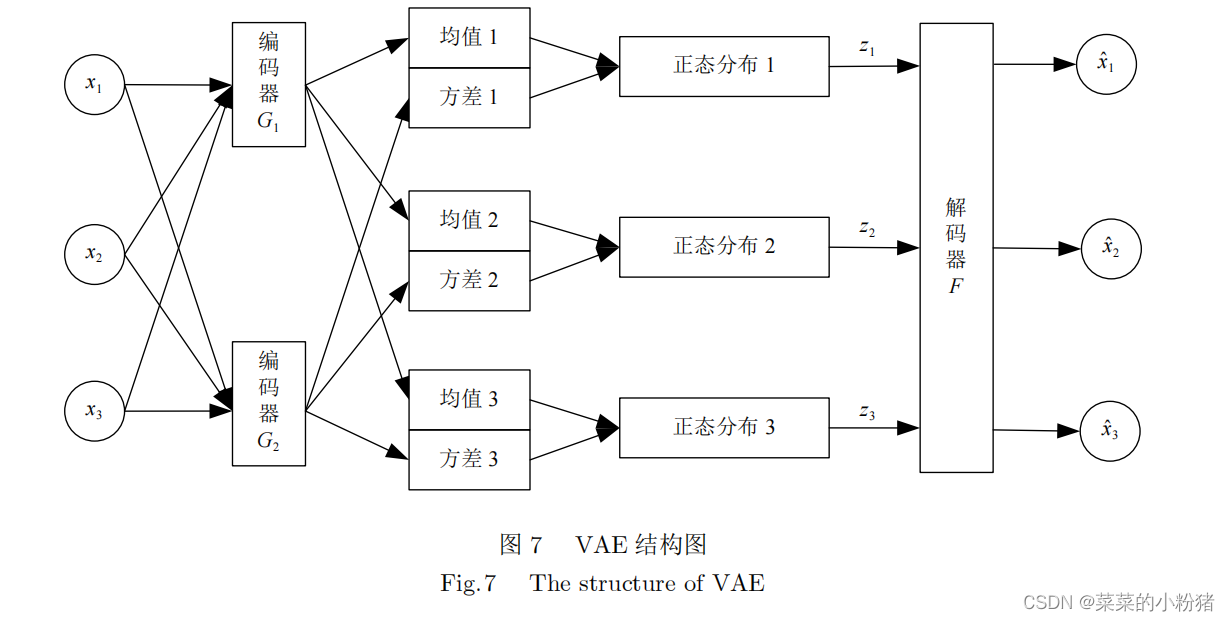
注：图来自于《胡铭菲, 左信, 刘建伟. 深度生成模型综述[J]. 自动化学报, 2022, 48(1): 40-74.》

VAE模型通过编码过程$Q(z|x)$将样本映射为隐藏变量$z$,并假设隐藏变量服从多元正太分布$P(x)\sim N(0,I)$,解码器$P(x|z)$从隐藏变量$z$中抽取样本,生成指定图像$\tilde{x}$。

2.理论推导

原始的样本数据$x$的概率分布：
$$P(x)={\int }_{z}P(x)P(x|z)dz$$
假设$z$服从标准高斯分布，先验分布$P(x|z)$属于高斯分布，即$x|z\sim N(\mu (z),\sigma (z))$。其中，$\mu (z)$和$\sigma (z)$是两个函数，分别是$z$对应的高斯分布的均值和方差（如下图),则$P(x)$就是再积分域上所有高斯分布的累加。

由于$P(z)$是已知的$P(x|z)$未知，所以求解问题实际上就是求$\mu (z)$, $\sigma (z)$这两个函数。我们最开始的目标是求解$P(x)$，且我们希望$P(x)$ 越大越好，这等价于求解关于$x$ 最大对数似然：
$$L=\sum _{x}logP(x)$$

2.1变分下界（Variational Lower bound）/变分推理

而$logP(x)$可变换为：
$$\begin{array}{r}\begin{array}{rl}logP(x)& ={\int }_{z}Q(z|x)logP(x)dz\\ & ={\int }_{z}Q(z|x)log\frac{P(z,x)}{P(z|x)}dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(z,x)}{Q(z|x)}\frac{Q(z|x)}{P(z|x)})dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(z,x)}{Q(z|x)})dz+{\int }_{z}Q(z|x)log(\frac{Q(z|x)}{P(z|x)})dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz+{\int }_{z}Q(z|x)log(\frac{Q(z|x)}{P(z|x)})dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz+KL(Q(z|x)||P(z|x))\end{array}\end{array}$$
注：${\int }_{z}Q(z|x)log(\frac{Q(z|x)}{P(z|x)})dz=KL(Q(z|x)||P(z|x)$ 查看生成模型基本概念：信息熵、交叉熵和相对熵（KL散度）
由于KL散度是大于0,可以得到：
$$logP(x)⩾{\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz$$
可得$logP(x)$下界$(Lower$ $bound)L_b$
$$L_b={\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz$$
原式可以表示为：
$$logP(x)=L_b+KL(Q(z|x)||P(z|x))$$

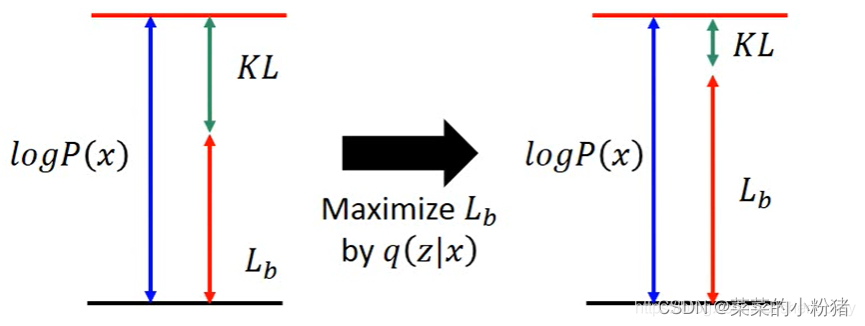
实际上，因为后验分布$P(z|x)$很难求(intractable)，所以才用$Q(z|x)$来逼近这个后验分布。由于$Q(z|x)$和$logP(x)$是完全没有关系的，$logP(x)$只跟$P(z|x)$有关，调节$Q(z|x)$是不会影响$logP(x)$。所以，调节$Q(z|x)$最大化下届$L_b$，KL则越小。
$$\begin{array}{r}\begin{array}{rl}{L}_b& ={\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(z)}{Q(z|x)})dz+{\int }_{z}Q(z|x)log(P(x|z))dz\\ & =-KL(Q(z|x)||P(z))+{\int }_{z}Q(z|x)log(P(x|z))dz\\ & =-KL(Q(z|x)||P(z))+E_{q(x|z)}[log(P(x|z))]\end{array}\end{array}$$
显然，最大化$L_b$等价于$min(-KL(Q(z|x)||P(z)))$和最大化$max(E_{q(x|z)}[log(P(x|z))])$

最小化KL散度

假设$P(z)$服从标准正太分布，且$Q(z|x)$服从高斯分布$N(\mu ,{\sigma }^2)$,于是代入计算可得：
$$\begin{array}{r}\begin{array}{rl}KL(Q(z|x)||P(z))& =KL(N(\mu ,{\sigma }^2)||N(0,1))\\ & =\int \frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}\left(log\frac{e^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}/\sqrt{2\pi {\sigma }^2}}{e^{\frac{-x^2}{2}}/\sqrt{2\pi }}\right)dx\\ & =\frac{1}{2}\frac{1}{\sqrt{2\pi {\sigma }^2}}\int e^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}(-log{\sigma }^2+x^2-\frac{(x-\mu {)}^2}{{\sigma }^2})dx\\ & =\frac{1}{2}\int \frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}(-log{\sigma }^2+x^2-\frac{(x-\mu {)}^2}{{\sigma }^2})dx\end{array}\end{array}$$
对上式中的积分进一步求解，$\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}$实际就是概率密度$f(x)$,而概率密度的为1.所以积分第一项等于$-log{\sigma }^2$;而又因为高斯分布的二阶矩就是$E(x^2)=\int x^{2}f(x)dx={\mu }^2+{\sigma }^2$,正好是对应积分第二项。有根据方差的定义可知$\sigma =\int (x-\mu )dx$,所以积分第三项为-1.
最终化简结果为：
$$\begin{array}{r}\begin{array}{rl}KL(Q(z|x)||P(z))& =KL(N(\mu ,{\sigma }^2)||N(0,1))\\ & =\frac{1}{2}(-log{\sigma }^2+{\mu }^2+{\sigma }^2-1)\end{array}\end{array}$$

最大化期望

也就是表明在给定$Q(z|x)$（编码器输出）的情况下 $P(x\mid z)$（解码器）输出的值尽可能高。具体来讲，第一步，利用encoder的神经网络计算出均值与方差，从中采样得到 $z$，这一过程就对应式子中的$Q(z|x)$；第二步，利用decoder的NN计算 $z$的均值方差，让均值（或也考虑方差）越接近 $x$ ，则产生$x$ 的几率 $logP(x|z)$ 越大，对应于式子中的最大化$logP(x|z)$ 这一部分。

具体代码如下：

    def loss_function(self,
                      *args,
                      **kwargs) -> dict:
        """
        Computes the VAE loss function.
        KL(N(\mu, \sigma), N(0, 1)) = \log \frac{1}{\sigma} + \frac{\sigma^2 + \mu^2}{2} - \frac{1}{2}
        :param args:
        :param kwargs:
        :return:
        """
        recons = args[0]
        input = args[1]
        mu = args[2]
        log_var = args[3]

        kld_weight = kwargs['M_N'] # Account for the minibatch samples from the dataset
        recons_loss =F.mse_loss(recons, input)
        kld_loss = torch.mean(-0.5 * torch.sum(1 + log_var - mu ** 2 - log_var.exp(), dim = 1), dim = 0)
        loss = recons_loss + kld_weight * kld_loss
        return {'loss': loss, 'Reconstruction_Loss':recons_loss.detach(), 'KLD':-kld_loss.detach()}

2.1重参数技巧（Reparameterization Trick）

最后模型在实现的时候，有一个重参数技巧，就是我们想从高斯分布$N(\mu ,{\sigma }^2)$ 中采样Z时，其实是相当于从$N(0,1)$中采样一个$ϵ$，然后再来计算$Z=\mu +ϵ\times \sigma$。这么做的原因是，采样这个操作是不可导的，而采样的结果是可导的，这样做个参数变换，$Z=\mu +ϵ\times \sigma$ 这个就可以参与梯度下降，模型就可以训练了。

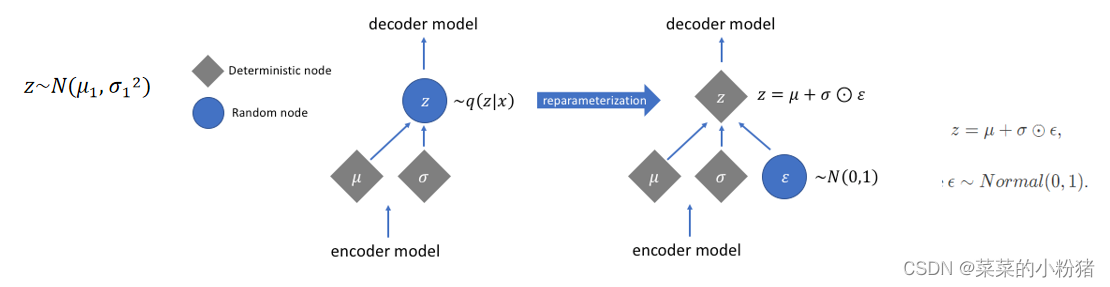
代码如下：

   def reparameterize(self, mu: Tensor, logvar: Tensor) -> Tensor:
        """
        Reparameterization trick to sample from N(mu, var) from
        N(0,1).
        :param mu: (Tensor) Mean of the latent Gaussian [B x D]
        :param logvar: (Tensor) Standard deviation of the latent Gaussian [B x D]
        :return: (Tensor) [B x D]
        """
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return eps * std + mu

反向传播过程：

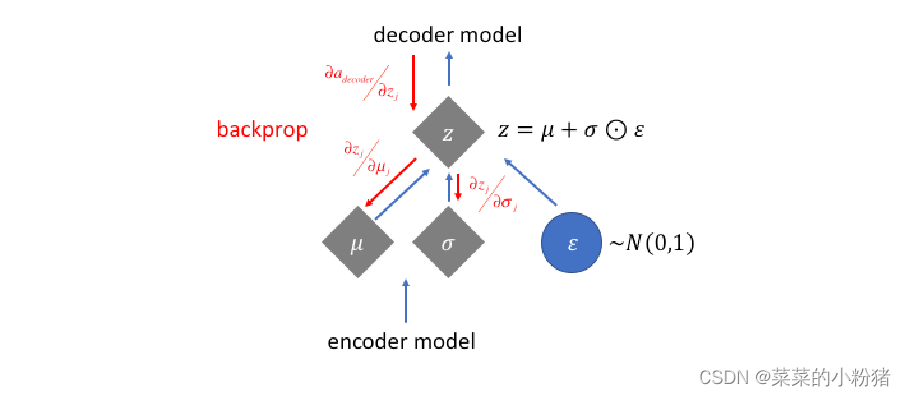
    def forward(self, input: Tensor, **kwargs) -> List[Tensor]:
        mu, log_var = self.encode(input)
        z = self.reparameterize(mu, log_var)
        return  [self.decode(z), input, mu, log_var]

应用及分析

在生成样本方面, VAE 类模型可以生成高清晰度的手写体数字、自然图像和人脸等基础数据, 并成功生成静态图片的未来预测图片,其中最有影响力的应用是在 VAE 的编码器和解码器中使用循环神经网络 RNN 的 DRAW 网络,DRAW 扩展了VAE的结构, 并且生成了逼真的门牌号码图片 (SVHN 数据集), 是 2016 年出现的效果最好的生成模型之一. DRAW 的作者随后在该模型中加入卷积网络提取空间信息, 进一步提高了模型的生成能力, 并生成了清晰的自然图像样本.除了生成图片样本, VAE 还可以在自然语言处理领域生成文本、在天文学中模拟对遥远星系的观测、在推荐系统中融合不同信息, 在图像合成领域生成不同属性的图像样本以及在化工领域中设计分子的结构等领域均有使用。
作为当前最常用的深度生成模型之一, VAE由于自身结构的固有缺点使模型生成的图片样本带有大量的噪声, 大部分 VAE 结构很难生成高清的图片样本, 在图像生成领域的效果不如基于 GAN和 FLOW 的生成模型, 所以在图像领域 VAE 通常被当作特征提取器. 但在自然语言处理领域, VAE类模型生成的语言样本比生成对抗网络更合理, 只需要简单的结构就能生成出较流畅的语言, 因此更应该在自然语言处理领域寻找VAE的优势之处。

参考资料

1.详解变分自编码器——VAE
2.李宏毅老师 Machine Learning (2017,秋，台湾大学) 国语

完整代码

click pytorch安装VAE项目详解 查看完整源码

初稿完成日期：2023.8.22（七夕节） 18:50