1. 离散Fourier变换的定义

一个信号 x 的离散Fourier变换(Discrete Fourier Transform，简记为DFT)定义为

$\displaystyle X(\omega_k) \triangleq \sum_{n=0}^{N-1}x(t_n)e^{-j \omega_k t_n} (k = 0,1 ,...,N - 1)$ ，

其逆(inverse) Fourier变换(简记为 IDFT)定义为

$\displaystyle x(t_n) =\frac{1}{N}\sum_{k=0}^{N-1}X(\omega_k)e^{j \omega_k t_n} (n = 0,1 ,...,N - 1)$ 。

(译注：符号“≜”表示“根据定义，左边等于右边”。)

其中，

$x (t_n) \triangleq$ 在时刻 $t_n$ (秒)时的输入信号的幅度(amplitude)。

$t_n \triangleq nT$ = 第n个采样时刻(instant)(秒)。

$n \triangleq$ 采样顺序编号(simple number)(整数)。

$T \triangleq$ 采样周期(simple period)(整数)。

$X(\omega_k) \triangleq$ 信号 x 在弧度频率(radian frequency)(译注：即，角频率) $\omega_k$ 处的频谱(spectrum)。

$\omega_k \triangleq k \Omega$ = 第 n 个频率样本(弧度/秒)。

$\Omega \triangleq \frac{2\pi}{NT}$ = 弧度频率采样间隔(sampling interval)。

$f_s \triangleq \frac{1}{T}$ = 采样率(sampling rate)(样本数/秒，或者Hz(Hertz))。

N = 时间和频率中的采样数目(整数)。

(译注：Hz的物理意义为“每秒循环次数(cycles per second)”)

2. 离散Fourier变换的数学知识

在信号处理的文献中，通常在前面的定义中令 T = 1, 从而获得更为纯粹的形式：

$\displaystyle X(k) \triangleq \sum_{n=0}^{N-1}x(n)e^{-j2\pi nk/N} (k = 0,1 ,...,N - 1)$ ,

$\displaystyle x(n) =\frac{1}{N}\sum_{k=0}^{N-1}X(k)e^{j 2\pi nk/N} (n = 0,1 ,...,N - 1)$ 。

其中，

$j \triangleq \sqrt{-1}$ (复数的基)

$\displaystyle e \triangleq \lim_{n \rightarrow \infty}(1+\frac{1}{n})^{n} = 2.71828182845905 ...$ 。

2.1 复平面

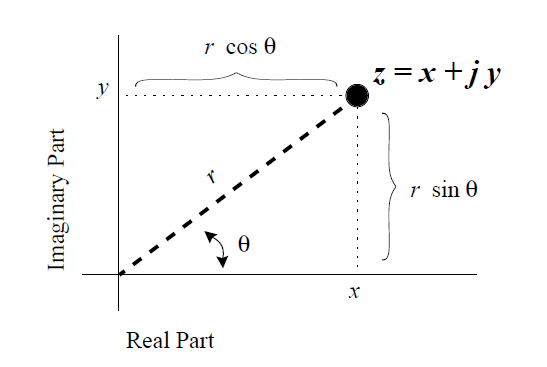
下面是一个点在复平面中的示意图：

--------------------------------------------图2.2. 复数在复平面中的图像-----------------------------------------

将 z = x + jy 绘制为复平面中的点 (x, y) 可以视为笛卡尔(Cartesian)坐标或直线坐标(rectilinear)中的绘图(译注：均有两个轴上的值相对应)。我们也可以根据极坐标将复数表示为一个有序对(r,θ),其中，r是原点到所绘点的距离，θ是数相对于正实数轴(按 y = 0 且 x > 0 所定义的直线)的夹角(如图2.2所示)。

使用初等几何知识，可以迅速地证明，从矩形坐标到极坐标的转换由下列公式完成：

$r = \sqrt{x^2+y^2}$ ,

$\theta = \tan^{-1}(\frac{y}{x})$ 。

第一个等式由 Pythagoras定理直接可推导出，第二个等式由tangent的定义可直接推导出。

$r \triangleq | z| = \sqrt{x^2+y^2 }$ = z 的(模(modulus)，大小(magnitude)，绝对值(absolute value),范数(norm)，或者半径(radius))(译注：对于复数而言，以上几种称谓是等效的)。

$\theta \triangleq \angle z = \tan^{-1}(\frac{y}{x})$ = z 的(角度(angle),参数(argument),相位(phase)) 。

z 的共轭复数用 $\overline{z}$ 表示，定义为

$\overline{z} \triangleq x - jy$ (译注：互为共轭的复数关于x轴对称)。

2.2 圆周运动(Circular Motion)

因为复数正弦的模是常量，因此，在复平面上，它一定位于圆周上。例如，

$x(t) = e^{j\omega t}$

在复平面上沿着单位圆画出逆时针(counter-clockwise)圆周运动的轨迹；而

$\overline{x(t)} = e^{-j\omega t}$

是顺时针(clockwise)的圆周运动。我们称形如 $e^{j\omega t}$ (ω > 0)的复数正弦函数为正频率正弦函数(positive-frequency sinusoid)，称形如 $e^{-j\omega t}$ 的复数正弦函数为负频率正弦函数(negative-frequency sinusoid)。注意，正负频率正弦函数一定是复数。

2.3 圆周运动的投影(Projection of Circular Motion)

单位圆在复平面上的方程可表示成 $z = e^{j\omega t}$ ,实部和虚部分别为

$\mathbf{Re}\{e^{j\omega t}\} = \cos(\omega t)$ ， $\mathbf{Im}\{e^{j\omega t}\} = \sin(\omega t)$ 。

在复平面上，可以将这个解释为正弦运动是圆周运动在任意直线上的投影。因此，正弦运动 $\cos(\omega t)$ 是圆周运动 $e^{j\omega t}$ 在实轴( x轴)上的投影，而正弦运动 $\sin(\omega t)$ 是圆周运动 $e^{j\omega t}$

在虚轴( y轴)上的投影。

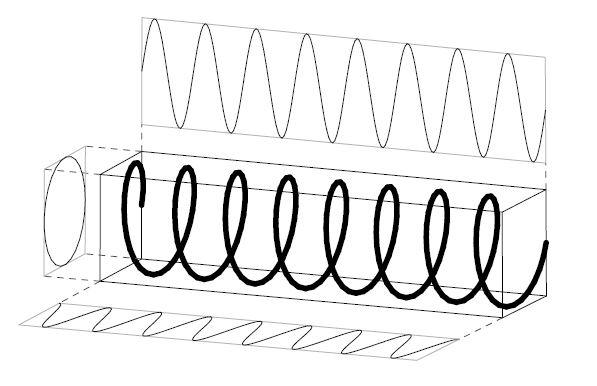
图 5.7 显示了复数正弦曲线与时间的关系图，以及它在坐标平面上的投影。这是显示 z 平面与时间的 3D 图。轴是实部、虚部和时间。(或者我们可以使用幅度和相位与时间的关系。)

-----------------------------------------------图 5.7 复数正弦曲线及期投影------------------------------------------

请注意，左侧投影(在 z 平面上)是一个圆，下部投影(实部与时间)是余弦，上部投影（虚部与时间）是正弦。穿过绘图的点在 z 平面上投影为匀速圆周运动，在其他两个平面上投影为正弦运动。

2.4 正负频率

根据Euler恒等式 $e^{j\theta} = \cos(\theta)+j\sin(\theta)$ ，我们可以得到

$\cos(\theta)=\frac{e^{j\theta}+e^{-j\theta}}{2}$ ,

$\sin(\theta)=\frac{e^{j\theta}-e^{-j\theta}}{2j}$ 。

令 $\theta = \omega t + \phi$ ，我们看到正弦和余弦(以及所有真正的正弦曲线)都由相等且相反的圆周运动之和组成。 换句话说，每个实正弦曲线都由正负频率分量的同等贡献组成。所有实信号都是如此。当我们进行频谱分析时，我们会发现每个实信号都包含等量的正频率和负频率，即，若用 X(ω)来表示实信号 x(t) 的频谱，我们总是有 | X(-ω)| = | X(ω)| 。

注意，在数学上，复数正弦 $Ae^{j(\omega t+\phi)}$ 确实比实数正弦 $A \sin(\omega t + \phi)$ 更简单且更基础。因为， $e^{j\omega t}$ 仅由一个频率组成，而 sin(ωt ) 实际上由两个频率 ω 和 –ω 组成。我们可以将实正弦曲线视为正频率和负频率复正弦曲线的总和，因此从这个意义上说，实正弦曲线是复正弦曲线的“复杂程度的两倍”。复数正弦曲线也更好，因为它们具有恒定的模量(constant modulus)。复正弦曲线的“幅度包络检测器(Amplitude envelope detectors)”很简单：只需计算实部和虚部平方和的平方根即可获得任意时刻的瞬时峰值幅度。频率解调器也同样微不足道：只需对复正弦曲线的相位进行微分即可获得其瞬时频率。因此，信号处理工程师通常更喜欢在进一步处理之前将实正弦曲线转换为复正弦曲线，这也就不足为奇了。

3. 内积与投影

内积(inner product)(或称点积)，可以看成一个信号y(.)(注：记法y(n)表示信号y在采样 n处的单个采样,而记法y(.)或者简单地记为 y 表示所有时间上的整个信号)在另一个信号x(.)上的投影。内积 <y,x> 计算的是 y 在 x上的投影系数(coefficient of projection)(注：信号 y 到另一个信号 x 的投影系数可以被认为是 y 中存在多少 x 的度量)。若 $x (n) = e^{j\omega_k nT} (n = 0 ,1 ,..,N - 1)$ (这是一个采样信号，单位幅度，0相位，复数正弦),假设选择角频率为 $\omega_k = 2\pi kf_{s}/N$ ，则内积计算的是离散Fourier变换(DFT)。对于 DFT ，具体的内积为

$\displaystyle <y, x> = \sum_{n=0}^{N-1}y(n)\overline{x (n)} = \sum_{n=0}^{N-1}y(n)e^{-j2\pi nk/N} \triangleq Y(\omega_k)$ 。

另一个常用的情况是离散时间Fourier变换(DTFT)，它与DFT类似，区别仅在于，它接收一个无限的采样数，而不是仅 N 个样本点。在这情况下，频率是连续的，并且

$\displaystyle <y, x> = \sum_{n=0}^{\infty}y(n)e^{-j\omega nT} \triangleq \mathbf{DTFT}_{\omega}(y)$

DTFT是当 DFT 中的样本数量接近无穷大时您得到的极限值。总和的下限保持为零，因为我们假设所有信号在负时间都为零。这意味着我们正在使用单边(unilateral)Fourier变换。还存在相应的双边变换(bilateral transform)，其求和下限为 -∞。

4. 理解离散Fourier变换

对于长度为N的复数序列x (n) (n = 0 ,1 ,...,N – 1)，其离散Fourier变换定义为

$\displaystyle X(\omega_k) \triangleq \sum_{n=0}^{N-1}x(n)e^{-j \omega_k t_n} =\sum_{n=0}^{N-1}x(n)e^{-j 2\pi kn/N}(k = 0,1 ,...,N - 1)$ 。

$t_n \triangleq nT$ = 第 n 个采样时刻(instant)(秒)。

$\omega_k \triangleq k\Omega$ = 第 k 个频率样本(弧度/秒)。

$T \triangleq 1/f_{s}$ = 时间采样间隔(秒)。

$\Omega \triangleq 2\pi f_{s}/N$ = 频率采样间隔(秒)。

现在，我们需要全面理解变换核(transform kernel),即

$e^{-j\omega_k t_n } = \cos(\omega_k t_n) - j \sin(\omega_k t_n)$ 。

这个变换内核由在 0 和采样率 $\omega_s \triangleq 2\pi f_s$ 之间均匀间隔的 N 个离散频率 $\omega_k$ 的复正弦曲线样本组成。

剩下的问题就是，理解x (n)乘以每个复数正弦曲线的逐点乘积在n上求和的目的和函数。我们将这种情况解释为内积运算，这个内积运算计算将信号x 投影到复数正弦曲线 $\cos(\omega_k t_n) - j \sin(\omega_k t_n)$ 上所产生的投影系数。因此，在 $\omega_k$ 处的离散Fourier变换 $X(\omega_k)$ 是一种复数正弦在那个用输入信号x所表示的频率处的幅度和相位的度量。这是所有变换和(以离散时间表示)与积分(以连续时间表示)和它们的核的基本函数。