目录

一. 基本术语

二. 广义表的性质

三. 广义表与线性表的区别和联系

四. 广义表的基本运算

一. 基本术语

广义表（又称列表Lists）是n>=0个元素的有限序列，其中每一个ai或者是原子，或者是一个广义表。

广义表通常记作：
其中：LS为表名，n为表的长度，每一个a_i为表的元素。习惯上，一般用大写字母表示广义表，小写字母表示原子。

表头：若LS非空(n>=1)，则其第一个元素就是表头。记作；

注：表头可以是原子，也可以是子表。
表尾：除表头之外的其它元素组成的表。记作；

注：表尾不是最后一个元素，而是一个子表。

例：(1)A=()；空表，长度为0。
(2)B=(())；长度为1，表头、表尾均为()。
(3)C=(a,(b,c))；长度为2，由原子a和子表(b,c)构成。表头为a；表尾为((b,c))。
(4)D=(x,y,z)；长度为3，每一项都是原子。表头为x；表尾为(y,z)。
(5) E=(C,D)；长度为2，每一项都是子表。表头为C；表尾为(D)。
(6)F=(a,F)；长度为2，第一项为原子，第二项为它本身。表头为a；表尾为F。F=(a, (a, (a, ...)))

二. 广义表的性质

(1)广义表中的数据元素有相对次序；一个直接前驱和一个直接后继；

(2)广义表的长度定义为最外层所包含元素的个数；如：C=(a, (b, c)是长度为2的广义表。
(3)广义表的深度定义为该广义表展开后所含括号的重数；如：A =(b)的深度为1，B=(A,d)的深度为2，C=(f,B,h)的深度为3。注意：“原子”的深度为0;“空表”的深度为1。
(4)广义表可以为其他广义表共享；如：广义表B就共享表A。在B中不必列出A的值，而是通过名称来引用，B= (A)。

(5)广义表可以是一个递归的表。如:F=(a, F)=(a, (a, (a...))
注意：此递归表的深度是无穷值，长度是有限值。

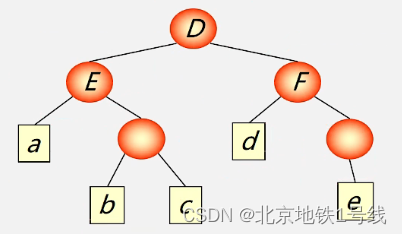
(6)广义表是多层次结构，广义表的元素可以是单元素，也可以是子表，而子表的元素还可以是子表。可以用图形象地表示。
例：D=(E,F)其中：E=(a, (b, c))，F=(d,(e))

三. 广义表与线性表的区别和联系

广义表可以看成是线性表的推广，线性表是广义表的特例。
广义表的结构相当灵活，在某种前提下，它可以兼容线性表、数组、树和有向图等各种常用的数据结构。当二维数组的每行（或每列)作为子表处理时，二维数组即为一个广义表。另外，树和有向图也可以用广义表来表示。
由于广义表不仅集中了线性表、数组、树和有向图等常见数据结构的特点，而且可有效地利用存储空间，因此在计算机的许多应用领域都有成功使用广义表的实例。

四. 广义表的基本运算

主要是求表头和表尾两种基本运算。

(1）求表头GetHead(L)：非空广义表的第一个元素，可以是一个原子也可以是一个子表；
(2）求表尾GetTail(L)：非空广义表除去表头元素以外其它元素所构成的表。表尾一定是一个表；
例：D= (E,F) = ((a, (b,c)),F)，则有：
GetHead(D)= E；GetTail(D)= (F)；GetHead(E) = a；GetTail(E)= ((b, c))；

GetHead(((b, c)))=(b, c)；GetTail(((b, c)))= ()；GetHead((b, c))=b；GetTail((b, c))= (c)
GetHead((c))= (c)；GetTail((c))= ()

请注意上面表达式里面各层括号的含义。