目录
交叉熵(Cross Entropy)
【预备知识】
【信息量】
【信息熵】
【相对熵】
【交叉熵】
交叉熵(Cross Entropy)
是Shannon信息论中一个重要概念,
主要用于度量两个概率分布间的差异性信息。
语言模型的性能通常用交叉熵和复杂度(perplexity)来衡量。交叉熵的意义是用该模型对文本识别的难度,或者从压缩的角度来看,每个词平均要用几个位来编码。复杂度的意义是用该模型表示这一文本平均的分支数,其倒数可视为每个词的平均概率。
平滑是指对没观察到的N元组合赋予一个概率值,以保证词序列总能通过语言模型得到一个概率值。通常使用的平滑技术有图灵估计、删除插值平滑、Katz平滑和Kneser-Ney平滑。
将交叉熵引入计算语言学消岐领域,采用语句的真实语义作为交叉熵的训练集的先验信息,将机器翻译的语义作为测试集后验信息。计算两者的交叉熵,并以交叉熵指导对歧义的辨识和消除。实例表明,该方法简洁有效.易于计算机自适应实现。交叉熵不失为计算语言学消岐的一种较为有效的工具。
交叉熵可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差所控制。
【预备知识】
1、信息量;
2、信息熵;
3、相对熵。
【信息量】
所谓信息量是指从N个相等可能事件中选出一个事件所需要的信息度量或含量,也就是在辩识N个事件中特定的一个事件的过程中所需要提问"是或否"的最少次数。在数学上,所传输的消息是其出现概率的单调下降函数。如从64个数中选定某一个数,提问:“是否大于32?”,则不论回答是与否,都消去了半数的可能事件,如此下去,只要问6次这类问题,就可以从64个数中选定一个数。我们可以用二进制的6个位来记录这一过程,就可以得到这条信息。
假设X是一个离散型随机变量,其取值集合为X,概率分布函数为p(x)=Pr(X=x),x∈X,我们定义事件X=x0的信息量为: I(x0)=−log(p(x0)),可以理解为,一个事件发生的概率越大,则它所携带的信息量就越小,而当p(x0)=1时,熵将等于0,也就是说该事件的发生不会导致任何信息量的增加。举个例子,小明平时不爱学习,考试经常不及格,而小王是个勤奋学习的好学生,经常得满分,所以我们可以做如下假设:
事件A:小明考试及格,对应的概率P(xA)=0.1,信息量为I(xA)=−log(0.1)=3.3219
事件B:小王考试及格,对应的概率P(xB)=0.999,信息量为I(xB)=−log(0.999)=0.0014
可以看出,结果非常符合直观:小明及格的可能性很低(十次考试只有一次及格),因此如果某次考试及格了(大家都会说:XXX竟然及格了!),必然会引入较大的信息量,对应的I值也较高。而对于小王而言,考试及格是大概率事件,在事件B发生前,大家普遍认为事件B的发生几乎是确定的,因此当某次考试小王及格这个事件发生时并不会引入太多的信息量,相应的I值也非常的低。
【信息熵】
信息理论的鼻祖之一Claude E. Shannon把信息(熵)定义为离散随机事件的出现概率。所谓信息熵,是一个数学上颇为抽象的概念,在这里不妨把信息熵理解成某种特定信息的出现概率。一般而言,当一种信息出现概率更高的时候,表明它被传播得更广泛,或者说,被引用的程度更高。我们可以认为,从信息传播的角度来看,信息熵可以表示信息的价值。为了求得信息的价值,我们通过求信息期望的方式,来求得信息熵。公式如下:H(x) = E[I(xi)] = E[ log(1/p(xi)) ] = -∑p(xi)log(p(xi)) 其中,x表示随机变量,与之相对应的是所有可能输出的集合,定义为符号集,随机变量的输出用x表示。P(x)表示输出概率函数。变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。为了保证有效性,这里约定当p(x)→0时,有p(x)logp(x)→0 。
当X为0-1分布时,熵与概率p的关系如下图:

可以看出,当两种取值的可能性相等时,不确定度最大(此时没有任何先验知识),这个结论可以推广到多种取值的情况。在图中也可以看出,当p=0或1时,熵为0,即此时X完全确定。 熵的单位随着公式中log运算的底数而变化,当底数为2时,单位为“比特”(bit),底数为e时,单位为“奈特”。
【相对熵】
相对熵,又称KL散度( Kullback–Leibler divergence),是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着D(P||Q) ≠ D(Q||P)。特别的,在信息论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,产生的信息损耗,其中P表示真实分布,Q表示P的拟合分布。有人将KL散度称为KL距离,但事实上,KL散度并不满足距离的概念,因为:(1)KL散度不是对称的;(2)KL散度不满足三角不等式。
设P(X)和Q(X)是X取值的两个离散概率分布,则P对Q的的相对熵为:
![]()
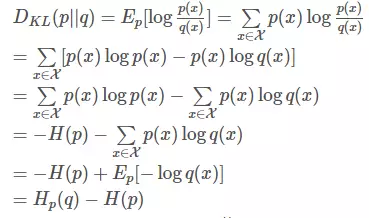
显然,当p=q 时,两者之间的相对熵DKL(p||q)=0 。上式最后的Hp(q)表示在p分布下,使用q进行编码需要的bit数,而H(p)表示对真实分布p所需要的最小编码bit数。基于此,相对熵的意义就很明确了:DKL(p||q)表示在真实分布为p的前提下,使用q分布进行编码相对于使用真实分布p进行编码(即最优编码)所多出来的bit数。并且为了保证连续性,做如下约定:
![]()
【交叉熵】
在信息论中,交叉熵是表示两个概率分布p,q,其中p表示真实分布,q表示非真实分布,在相同的一组事件中,其中,用非真实分布q来表示某个事件发生所需要的平均比特数。从这个定义中,我们很难理解交叉熵的定义。
假设现在有一个样本集中两个概率分布p,q,其中p为真实分布,q为非真实分布。假如,按照真实分布p来衡量识别一个样本所需要的编码长度的期望为:
H(p)=
![]()
但是,如果非真实分布q来表示来自真实分布p的平均编码长度,则应该是:
H(p,q)=
![]()
此时就将H(p,q)称之为交叉熵。交叉熵的计算方式如下:
CEH(p,q)=
![]()
![]()
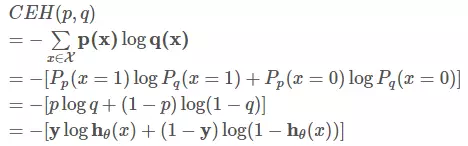
对所有训练样本取均值得:
![]()