目录

343. 整数拆分

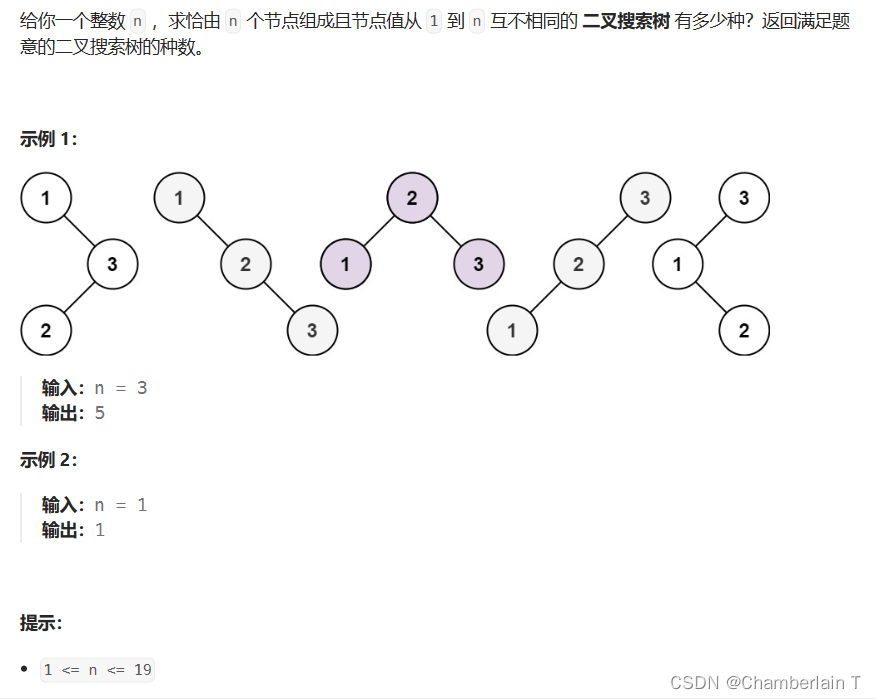
96. 不同的二叉搜索树

---

343. 整数拆分

类型：动态规划

难度：medium

 

思路：

        dp[i]所用的拆分方法至少已经拆分了两次，比如dp[2]=1，小于2，在大于2的数中，最后的2是不会拆的。

 

代码：

// // 贪心
// // 以3为单位进行拆分，最后剩余小于等于4，则直接乘
class Solution {
    public int integerBreak(int n) {
        if (n == 2) {
            return 1;
        }
        if (n == 3) {
            return 2;
        }
        if (n == 4) {
            return 4;
        }
        int max = 1;
        while (n > 4) {
            max *= 3;
            n -= 3;
        }
        max *= n;
        return max;
    }
}

// 动态规划
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            // j <= i / 2为剪枝，也可以j < i
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

96. 不同的二叉搜索树

类型：动态规划

难度：medium

 

思路：

        dp[i]指节点个数为i时，有多少种类二叉树。

        dp[3] = dp[0] * dp[2] + dp[1] * dp[1] + dp[2] * dp[0] 

        dp[4] = dp[0] * dp[3] + dp[1] * dp[2] + dp[2] * dp[1] + dp[3] * dp[0]

        就是左子树种类乘以右子树种类的累加；

代码：

class Solution {
    public int numTrees(int n) {
        if (n <= 2) {
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                dp[i] += dp[j] * dp[i - 1 - j];
            }
        }
        return dp[n];
    }
}