1.创建并计算多项式
此示例说明如何在 MATLAB® 中将多项式表示为向量以及根据相关点计算多项式。
1.1 表示多项式
MATLAB® 将多项式表示为行向量,其中包含按降幂排序的系数。例如,三元素向量
p = [p2 p1 p0];
表示多项式
创建一个向量以表示二次多项式
 。
。
p = [1 -4 4];
此外,还必须将系数为 0
的多项式中间项输入到该向量中,因为
0
用作 x 的特定幂的占位符。 创建一个向量来表示多项式
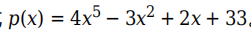 。
。
p = [4 0 0 -3 2 33];
1.2 多项式的计算
将多项式作为向量输入到 MATLAB® 后,请使用 polyval
函数根据特定值计算多项式。
使用
polyval
计算
p
(2)
。
polyval(p,2)
ans = 153
您也可以使用 polyvalm 以矩阵方式计算多项式。一个变量中的多项式表达式

将变为矩阵表达式
其中,X
是方阵,
I
是单位矩阵。
创建方阵 X
并根据
X
计算
p
。
X = [2 4 5; -1 0 3; 7 1 5];
Y = polyvalm(p,X)
Y = 3×3
154392 78561 193065
49001 24104 59692
215378 111419 269614
2.多项式的根
此示例演示如何通过多种不同的方法计算多项式的根。
2.1 数值根
roots 函数用于计算系数向量表示的单变量多项式的根。 例如,创建一个向量以表示多项式
x²
−
x
− 6
,然后计算多项式的根。
p = [1 -1 -6];
r = roots(p)
r =
3
-2
按照惯例,MATLAB 以列向量形式返回这些根。
poly 函数将这些根重新转换为多项式系数。对向量执行运算时,
poly
和
roots 为逆函数,因此poly(roots(p))
返回
p
(取决于舍入误差、排序和缩放)。
p2 = poly(r)
p2 =
1 -1 -6
对矩阵执行运算时,poly 函数会计算矩阵的特征多项式。特征多项式的根是矩阵的特征值。因此,roots(poly(A))
和
eig(A)
返回相同的答案(取决于舍入误差、排序和缩放)。
2.2 使用代换法求根
您可以通过使用代换法简化方程来对涉及三角函数的多项式方程求解。一个变量的生成多项式不再包含任何三角函数。
例如,计算 θ
用于对该方程进行求解的值
3cos
²
(
θ
) − sin(
θ
) + 3 = 0 .
利用 cos²(θ) = 1 − sin²(θ)
,完全以正弦函数的方式表示该方程:
−3sin²(θ
) − sin(
θ
) + 6 = 0 .
利用代换法 x
= sin(
θ
)
,将该方程表示为简单的多项式方程:
−3x² −
x
+ 6 = 0 .
创建一个向量以表示多项式。
p = [-3 -1 6];
求多项式的根。
r = roots(p)
r = 2×1
-1.5907
1.2573
要撤消代换法,请使用 θ
= sin
−1
(
x
)
。
asin
函数计算反正弦。
theta = asin(r)
theta = 2×1 complex
-1.5708 + 1.0395i
1.5708 - 0.7028i
验证 theta
中的元素是否为
θ
中用来对原始方程求解的值(在舍入误差内)。
f = @(Z) 3*cos(Z).^2 - sin(Z) + 3;
f(theta)
ans = 2×1 complex
10
-14
×
-0.0888 + 0.0647i
0.2665 + 0.0399i
2.3 特定区间内的根
使用 fzero 函数求多项式在特定区间内的根。在其他使用情况下,如果您绘制多项式并想要知道特定根的值,则这种方法很适用。
例如,创建一个函数句柄以表示多项式

p = @(x) 3*x.^7 + 4*x.^6 + 2*x.^5 + 4*x.^4 + x.^3 + 5*x.^2;
在区间 [ − 2, 1]
内绘制该函数。
x = -2:0.1:1;
plot(x,p(x))
ylim([-100 50])
grid
on
hold
on

从绘图中可以看到,多项式在 0
和另一个接近
-1.5
的位置各有一个简单的根。使用
fzero
计算并绘制接近
-1.5 的根。
Z = fzero(p, -1.5)
Z = -1.6056
plot(Z,p(Z),
'r*'
)

2.4 符号根
如果您有 Symbolic Math Toolbox™,则还会提供以符号形式计算多项式的其他选项。一种方式是使用solve
函数。
syms
x
s = solve(x^2-x-6)
s =
-2
3
另一种方式是使用 factor
函数计算多项式各项的因子。
F = factor(x^2-x-6)
F =
[ x + 2, x - 3]
3.对多项式求积分和微分
此示例演示如何使用 polyint
和
polyder 函数对由系数向量表示的任何多项式求解析积分或微分。使用 polyder 获取多项式
 的导数。生成的多项式为
的导数。生成的多项式为

p = [1 0 -2 -5];
q = polyder(p)
q = 1×3
3 0 -2
同样,使用 polyint 对多项式
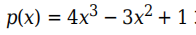 求积分。生成的多项式为
求积分。生成的多项式为
p = [4 -3 0 1];
q = polyint(p)
q = 1×5
1 -1 0 1 0
polyder 也可以计算两个多项式积或商的导数。例如,创建两个向量来表示多项式a
(
x
) =
x²
+ 3
x
+ 5
和
b
(
x
) = 2x²
+ 4
x
+ 6
。
a = [1 3 5];
b = [2 4 6];
通过调用带有单个输出参数的 polyder 来计算导数


c = polyder(a,b)
c = 1×4
8 30 56 38
通过调用带有两个输出参数的 polyder 来计算导数
 生成的多项式为
生成的多项式为
 生成的多项式为
生成的多项式为
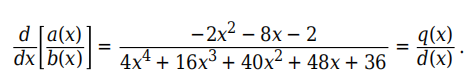
[q,d] = polyder(a,b)
q = 1×3
-2 -8 -2
d = 1×5
4 16 40 48 36