题目

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

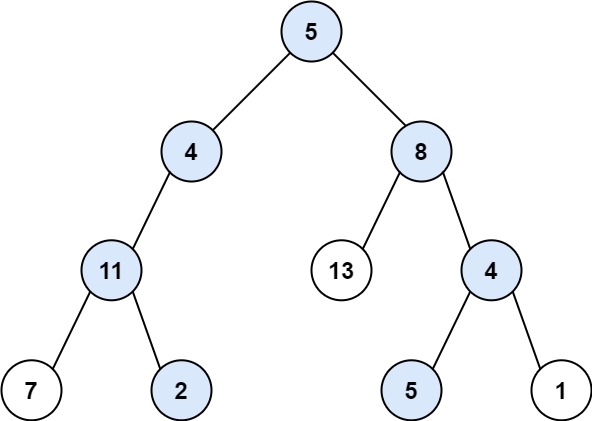
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

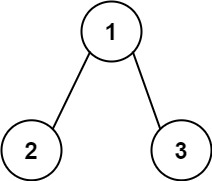
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

解题思路

1.题目要求我们找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。我们可以使用深度优先遍历来解决这个问题。

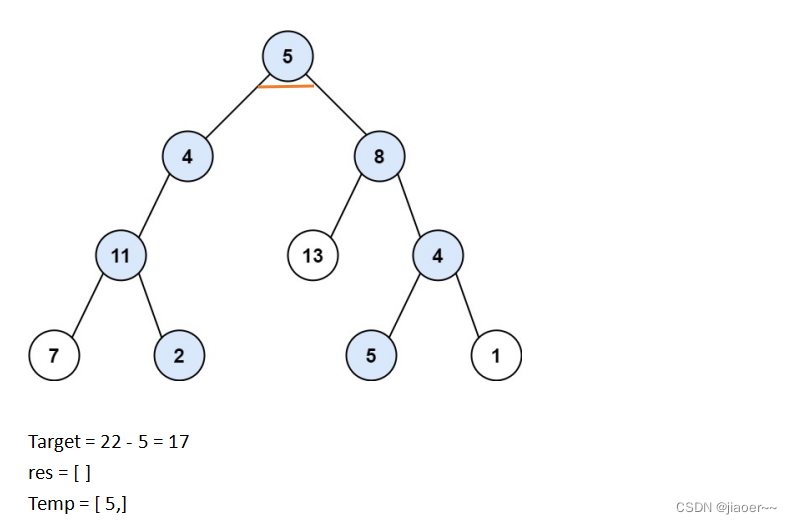
2.举个例子：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22

首先我们建立两个动态数组res和temp来存储结果和遍历的路径。

然后我们从根节点开始遍历，先将 5 放入数组 temp ，并且给 target 减 5 。

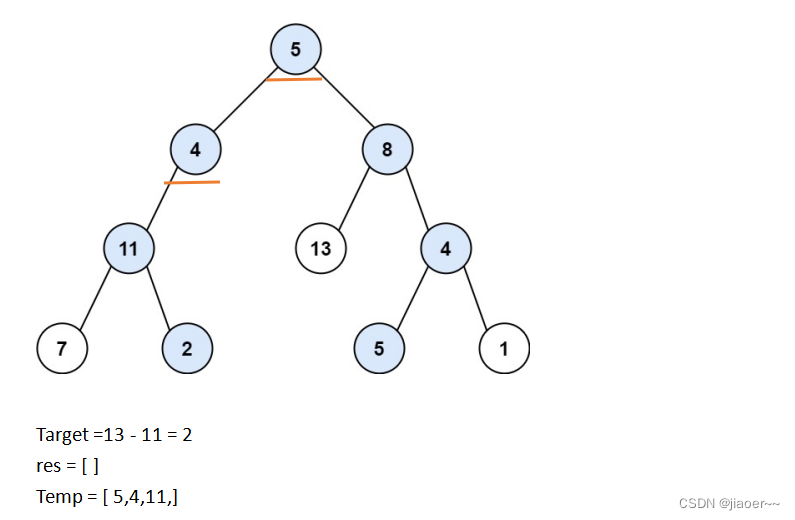
此时 target 不为 0 ，那么我们需要继续遍历，再将 5 的左孩子 4 放入temp 中，并且给 target 减 4。

此时 target 不为 0 ，那么我们需要继续遍历，再将 4 的左孩子 11 放入temp 中，并且给 target 减 11。

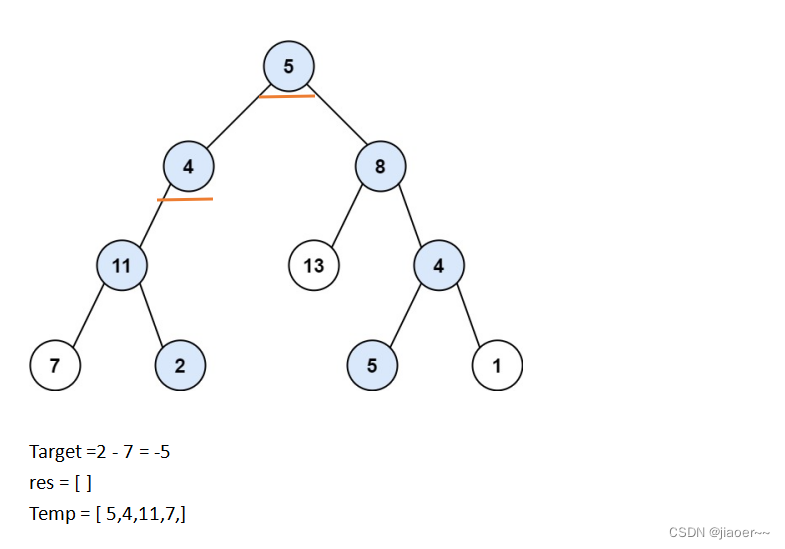
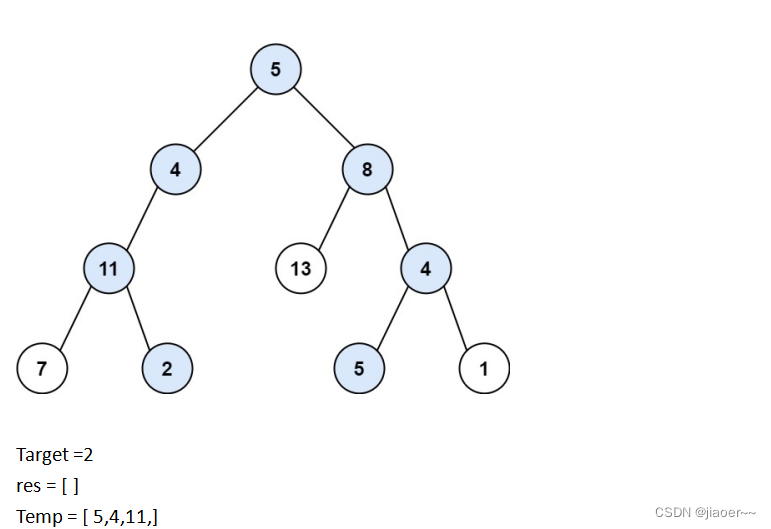
此时 target 不为 0 ，那么我们需要继续遍历，再将 11 的左孩子 7 放入temp 中，并且给 target 减 11。

这时我们发现 7 已经是叶子节点，但是target还是不为 0 ，那就说明这条路不是路径总和等于给定目标和的路径，我们就需要回溯，我们返回上一个节点，也就是11。

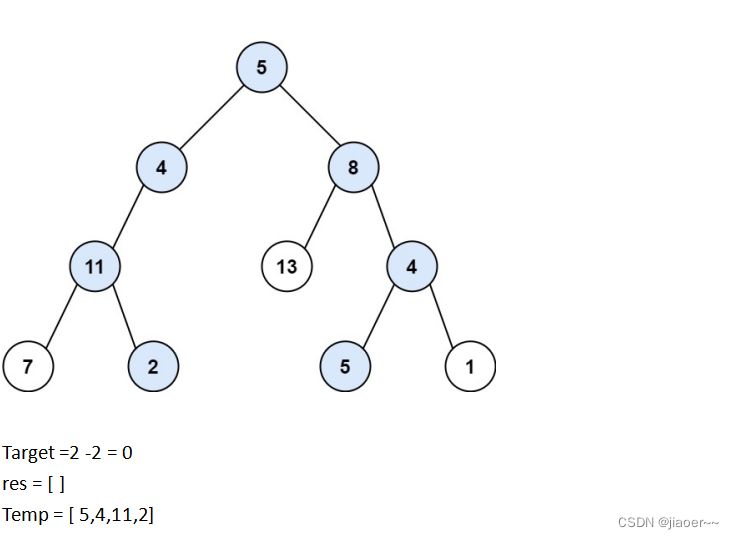
然后我们去遍历 11 的右孩子 2 ，将 11 的右孩子 2 放入temp 中，并且给 target 减 2。

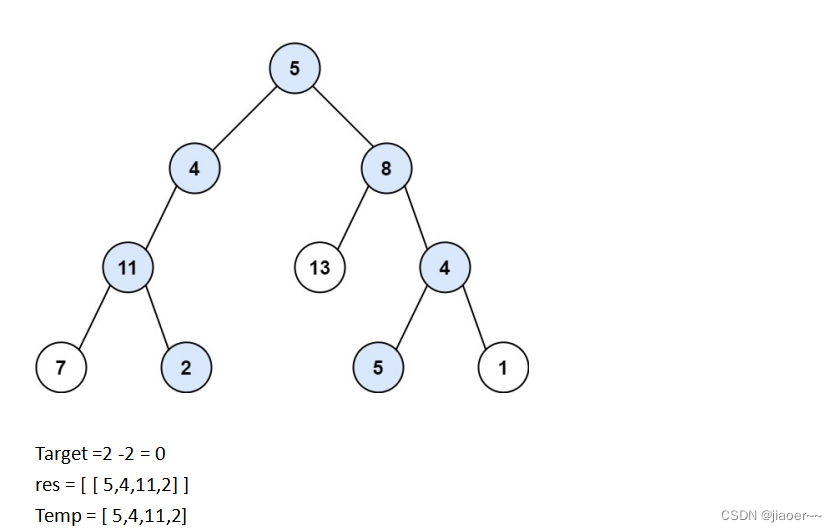
此时 target 刚好为 0 ，并且 2 也是叶子节点，那就说明我们找到了路径总和等于给定目标和的路径，我们需要将 temp 中保存的路径放入数组 res 中，

然后再进行回溯按照相同的思路去遍历其他的节点，直到所有节点都遍历结束，最后返回 res即可。

代码实现

class Solution {
    List<List<Integer>> res;
    List<Integer> temp;
    public List<List<Integer>> pathSum(TreeNode root, int target) {
        res = new ArrayList<>();
        temp = new ArrayList<>();
        dsf(root,target);
        return res;
    }
    void dsf(TreeNode root, int target){
        if(root == null){
            return;
        }
        temp.add(root.val);
        target = target - root.val;
        if(root.left == null && root.right == null && target == 0){
            res.add(new ArrayList(temp));
        }
        dsf(root.left, target);
        dsf(root.right, target);
        temp.remove(temp.size()-1);
}
}