目录
回溯算法详解
回溯VS递归
回溯算法的实现过程
n个结点构造多本节要讨论的是当给定 n(n>=0)个结点时,可以构建多少种形态不同的树。
回溯算法详解
回溯算法,又称为“试探法”。解决问题时,每进行一步,都是抱着试试看的态度,如果发现当前选择并不是最好的,或者这么走下去肯定达不到目标,立刻做回退操作重新选择。这种走不通就回退再走的方法就是回溯算法。
例如,在解决列举集合 {1,2,3} 中所有子集的问题中,就可以使用回溯算法。从集合的开头元素开始,对每个元素都有两种选择:取还是舍。当确定了一个元素的取舍之后,再进行下一个元素,直到集合最后一个元素。其中的每个操作都可以看作是一次尝试,每次尝试都可以得出一个结果。将得到的结果综合起来,就是集合的所有子集。
实现代码为:
- #include <stdio.h>
- //设置一个数组,数组的下标表示集合中的元素,所以数组只用下标为1,2,3的空间
- int set[5];
- //i代表数组下标,n表示集合中最大的元素值
- void PowerSet(int i,int n){
- //当i>n时,说明集合中所有的元素都做了选择,开始判断
- if (i>n) {
- for (int j=1; j<=n; j++) {
- //如果树组中存放的是 1,说明在当初尝试时,选择取该元素,即对应的数组下标,所以,可以输出
- if (set[j]==1) {
- printf("%d ",j);
- }
- }
- printf("\n");
- }else{
- //如果选择要该元素,对应的数组单元中赋值为1;反之,赋值为0。然后继续向下探索
- set[i]=1;PowerSet(i+1, n);
- set[i]=0;PowerSet(i+1, n);
- }
- }
- int main() {
- int n=3;
- for (int i=0; i<5; i++) {
- set[i]=0;
- }
- PowerSet(1, n);
- return 0;
- }
运行结果:
1 2 3
1 2
1 3
1
2 3
2
3
回溯VS递归
很多人认为回溯和递归是一样的,其实不然。在回溯法中可以看到有递归的身影,但是两者是有区别的。
回溯法从问题本身出发,寻找可能实现的所有情况。和穷举法的思想相近,不同在于穷举法是将所有的情况都列举出来以后再一一筛选,而回溯法在列举过程如果发现当前情况根本不可能存在,就停止后续的所有工作,返回上一步进行新的尝试。
递归是从问题的结果出发,例如求 n!,要想知道 n!的结果,就需要知道 n*(n-1)! 的结果,而要想知道 (n-1)! 结果,就需要提前知道 (n-1)*(n-2)!。这样不断地向自己提问,不断地调用自己的思想就是递归。
回溯和递归唯一的联系就是,回溯法可以用递归思想实现。
回溯算法的实现过程
使用回溯法解决问题的过程,实际上是建立一棵“状态树”的过程。例如,在解决列举集合{1,2,3}所有子集的问题中,对于每个元素,都有两种状态,取还是舍,所以构建的状态树为:
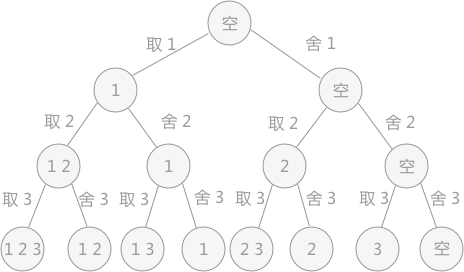
图1 状态树
回溯算法的求解过程实质上是先序遍历“状态树”的过程。树中每一个叶子结点,都有可能是问题的答案。图 1 中的状态树是满二叉树,得到的叶子结点全部都是问题的解。
在某些情况下,回溯算法解决问题的过程中创建的状态树并不都是满二叉树,因为在试探的过程中,有时会发现此种情况下,再往下进行没有意义,所以会放弃这条死路,回溯到上一步。在树中的体现,就是在树的最后一层不是满的,即不是满二叉树,需要自己判断哪些叶子结点代表的是正确的结果。
n个结点构造多本节要讨论的是当给定 n(n>=0)个结点时,可以构建多少种形态不同的树。
如果两棵树中各个结点的位置都一一对应,可以说这两棵树相似。如果两棵树不仅相似,而且对应结点上的数据也相同,就可以说这两棵树等价。本节中,形态不同的树指的是互不相似的树。
前面介绍过,对于任意一棵普通树,通过孩子兄弟表示法的转化,都可以找到唯一的一棵二叉树与之对应。所以本节研究的题目也可以转化成:n 个结点可以构建多少种形态不同的二叉树。
每一棵普通树对应的都是一棵没有右子树的二叉树,所以对于 n 个结点的树来说,树的形态改变是因为除了根结点之外的其它结点改变形态得到的,所以,n 个结点构建的形态不同的树与之对应的是 n-1 个结点构建的形态不同的二叉树。
如果 tn 表示 n 个结点构建的形态不同的树的数量,bn 表示 n 个结点构建的形态不同的二叉树的数量,则两者之间有这样的关系:tn=bn-1。
【方法一】
最直接的一种方法就是推理。当 n=0 时,只能构建一棵空树;当 n=2 时,可以构建 2 棵形态不同的二叉树,如图 1(A);当 n=3 时,可以构建 5 棵形态互不相同的二叉树,如图 1(B)。
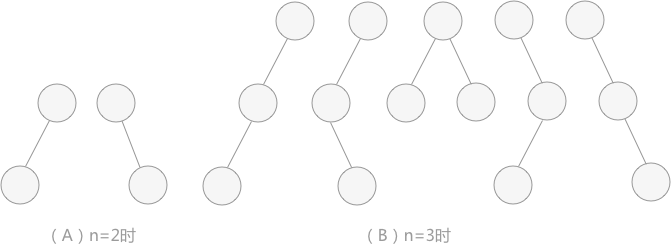
图 1 不同形态的二叉树
对于具有 n( n>1 )个结点的二叉树来说,都可以看成是一个根结点、由 i 个结点组成的左子树和由 n-i-1 个结点组成的右子树。
当 n=1 时,也适用,只不过只有一个根结点,没有左右孩子(i=0)。
可以得出一个递推公式:
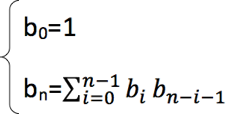
通过对公式一步步的数学推算,最后得出,含有 n 个结点的不相似的二叉树的数量为:
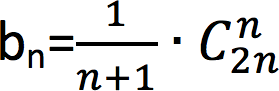
【方法二】
从遍历二叉树的角度进行分析,对于任意一棵二叉树来说,它的前序序列和中序序列以及后序序列都是唯一的。其实是这句话还可以倒过来说,只要确定了一棵二叉树的三种遍历序列中的两种,那么这棵二叉树也可以唯一确定。
例如,给定了一个二叉树的前序序列和中序序列分别为:
前序序列:A B C D E F G
中序序列:C B E D A F G
可以唯一得到的二叉树如图 2(4):
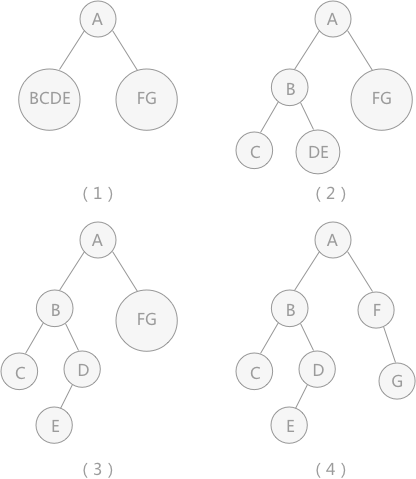
图 2 构造二叉树的过程示意图
分析:通过前序序列得知,结点A为二叉树的根结点,结合中序序列,在结点 A 左侧的肯定为其左孩子中的所有结点,右边为右孩子的所有结点,如图 2(1)所示。
再分析 A 结点的左孩子,在前序序列看到,结点 A 后紧跟的是结点 B,由此断定结点 A 的左孩子是 B,再看中序序列,结点 B 左侧只有一个结点 C ,为 B 的左孩子,结点 B 右侧的结点E 和 D 为右孩子,如图 2(2)。
再分析结点 B 的右孩子,前序序列看到,结点 D 在 E 的前边,所有 D 为 B 的右孩子。在中序序列中,结点 E 在 D 前边,说明 E 是 D 的左孩子,如图 2(3)。
最后分析结点 A 的右孩子,由前序序列看到, F 在 G 前边,说明F为根结点。在中序序列中也是如此,说明,G 是 F 的右孩子。如图 2(4)所示。
如果要唯一确定一棵二叉树,必须知道至少两种遍历序列。如果只确定一种序列,无法准确判定二叉树的具体构造。
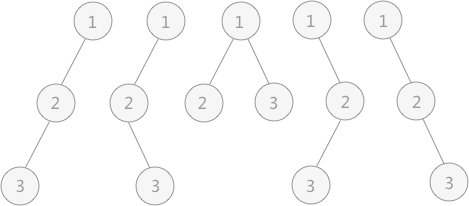
图 3 前序序列(1,2,3)的二叉树
如图 3 所示为前序序列(1,2,3)构建的不同形态的二叉树,他们的中序序列各不相同。所以不同形态二叉树的数目恰好就是前序序列一定的情况下,所能得到的不同的中序序列的个数。
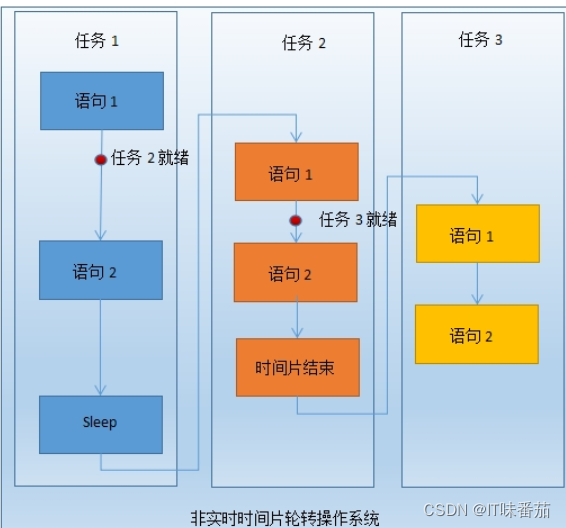
中序序列是对二叉树进行中序遍历获得的,遍历的过程实质上就是结点数据进栈出栈的过程。所以,中序序列的个数就是数列(1,2,3)按1-2-3的顺序进栈,各元素选择在不同的时间点出栈,所获的的不同的出栈顺序即为中序序列,而中序序列的数目,也就是不同形态的二叉树的个数。
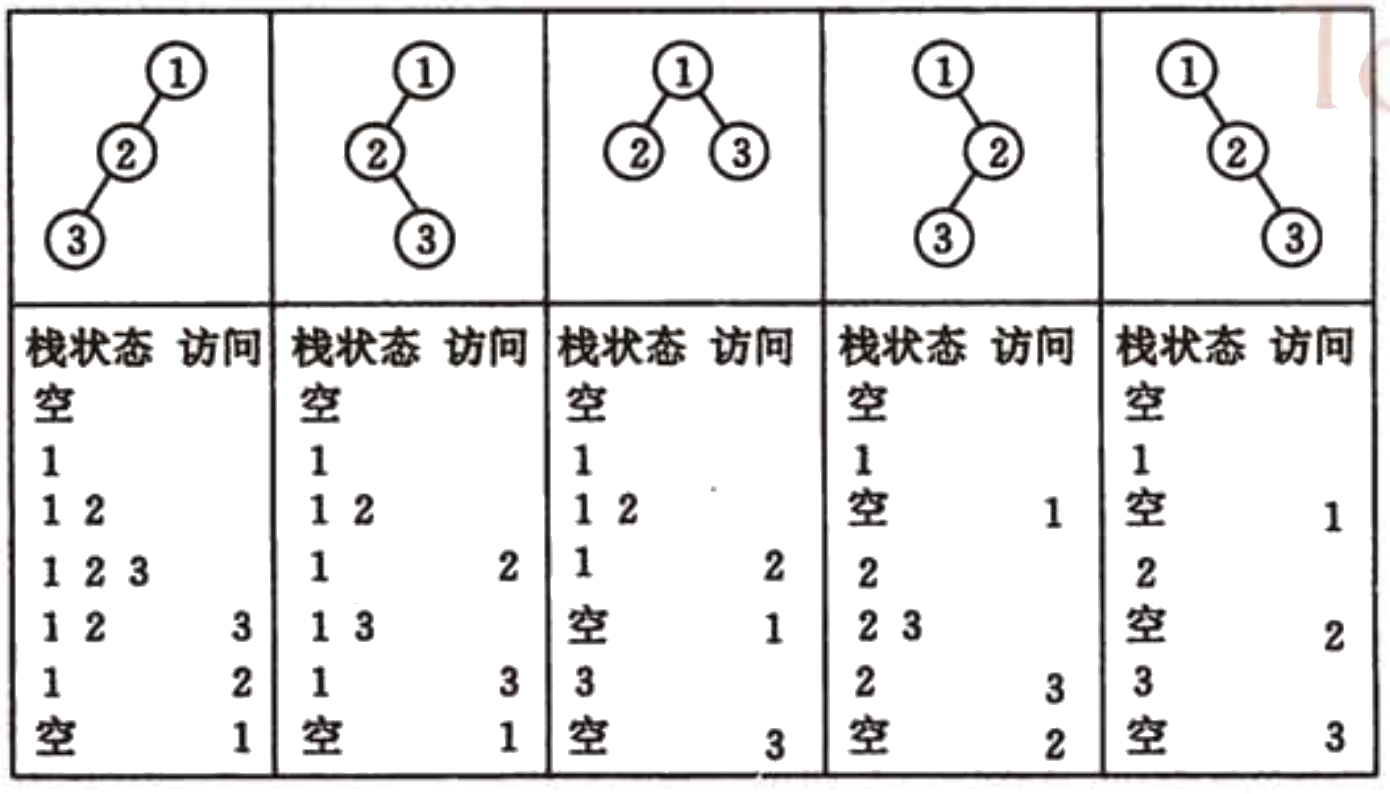
图 4 中序遍历时进栈和出栈的过程
根据数列中数据的个数 n,所得到的排列顺序的数目为:
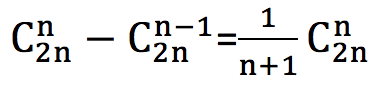
通过以上两种方式,都可以知道 n 个结点能构建的不同形态的二叉树的数量,再结合 tn=bn-1,就可以计算出 n 个结点能构建的不同形态的树的个数。