一、BF匹配
BF算法中的BF是Brute Force的缩写,中文叫作暴力匹配算法,也叫朴素匹配算法。
BF算法的时间复杂度很高,是O(nm),但在实际的开发中,它却是一个比较常用的字符串匹配算法。
第一,实际的软件开发中,大部分情况下,模式串和主串的长度都不会太大。而且每次模式串与主串中的子串匹配的时候,当中途遇到不能匹配的字符的时候,就可以就停止了,不需要把m个字符都对比一下。所以,尽管理论上的最坏情况时间复杂度是O(nm),但是,统计意义上,大部分情况下,算法执行效率要比这个高很多。
第二,朴素字符串匹配算法思想简单,代码实现也非常简单。简单意味着不容易出错,如果有bug也容易暴露和修复。在工程中,在满性性能要求的前提下,简单是首选。
public class BFMate {
public static void main(String[] args) {
BFMate("adjhkljabclkffkk","abc");
}
public static boolean BFMate(String mainStr,String modelStr) {
int len = mainStr.length()-modelStr.length();
for(int i=0;i<len;i++) {
if(modelStr.equals(mainStr.substring(i, i+modelStr.length()))) {
System.out.println("main=="+mainStr.substring(i, i+modelStr.length()));
return true;
}
}
return false;
}
}
二、BM匹配
BM(Boyer-Moore)算法。它是一种非常高效的字符串匹配算法。
BM算法核心思想是,利用模式串本身的特点,在模式串中某个字符与主串不能匹配的时候,将模式串往后多滑动几位,以此来减少不必要的字符比较,提高匹配的效率。BM算法构建的规则有两类,字符规则和好后缀规则。好后缀规则可以独立于坏字符规则使用。因为坏字符规则的实现比较耗内存,为了节省内存,我们可以只用好后缀规则来实现BM算法。
public class BMMate {
private final int Size = 256;
public void generateBC(char[] b,int m,int[] bc) {
for(int i=0;i<Size;i++) {
bc[i] = -1;//初始化bc
}
for(int i=0;i<=m;i++) {
int ascii = (int)b[i];//计算b[i]的ASCII值
bc[ascii] = i;//b[i]在bc中的位置
}
}
//b表示模式串,m表示长度,suffix、prefix数组事先申请好了
private static void generateGS(char[] b,int m,int[] suffix,boolean[] prefix) {
for(int i=0;i<m;i++) {//初始化
suffix[i] = -1;
prefix[i] = false;
}
for(int i=0;i<m-1;i++) {//b[0,i]
int j=i;
int k=0;//公共后缀子串长度
while(j>=0&&(b[j] == b[m-1-k])) {//与b[0,m-1]求公共后缀子串
--j;
++k;
suffix[k]=j+1;//j+1表示公共后缀子串在b[0,i]中的起始下标
System.out.println("i="+i+",j="+j);
System.out.println("suffix"+k+"="+suffix[k]);
}
if(j==-1) {
prefix[k] = true;//如果公共后缀子串也是模式串的前缀子串
System.out.println("prefix"+k+"="+prefix[k]);
}
}
}
public int bm(char[] a,int n,char[] b,int m) {
int [] bc = new int[Size];//记录模式串中每个字符最后出现的位置
generateBC(b,m,bc);//构建坏字符哈希表
int[] suffix = new int[m];
boolean[] prefix = new boolean[m];
generateGS(b,m,suffix,prefix);
int i=0;//表示主串与模式串第一个字符对齐
while(i<n-m) {
int j=0;
for(j=m-1;j>=0;j--) {//模式串从后往前匹配
if(a[i+j] != b[j]) break;
}
if(j<=0) return i;//匹配成功,返回主串与模式串第一个匹配字符的位置
int x = j-bc[(int)a[i+j]];
int y = 0;
if(j<m-1) {//如果有好后缀的话
y = moveByGS(j,m,suffix,prefix);
}
i = i+Math.max(x, y);
}
return -1;
}
//j表示坏字符对应的模式串中的字符下标;m表示模式串长度
private int moveByGS(int j,int m,int[] suffix,boolean[] prefix) {
int k=m-1-j;//好后缀长度
if(suffix[k] != -1) {
return j-suffix[k]+1;
}
for(int r = j+2;r<=m-1;++r) {
if(prefix[m-r]==true) {
return r;
}
}
return m;
}
}
三、Trie树
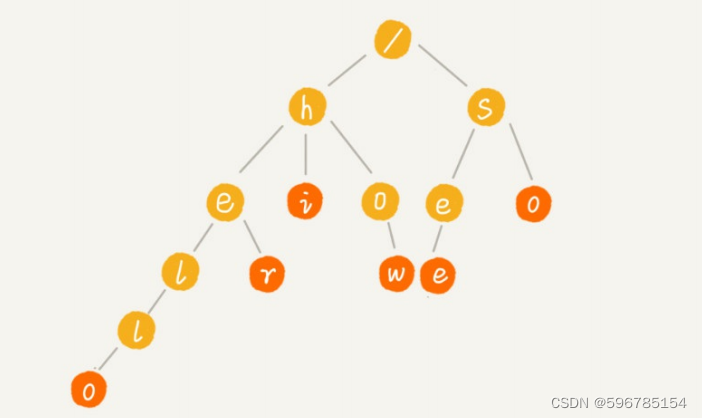
Trie树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
/**
* 假设插入的数据只包含26个小写字母组成的单词
* 将26个字母映射的一个长度26的数组中,下标0-25分别对应a-z
*
* 插入字符串时间复杂度 : O(n),n表示所有字符串的长度和
* 查找字符串时间复杂度 : O(k),k表示要查找的字符串的长度
*
* Trie树不适合精确匹配查找,这种问题更适合用散列表或者红黑树来解决。
* Trie树比较适合的是查找前缀匹配的字符串,类似实现搜索关键词的提示功能。
*/
public class TrieTree {
private TrieNode root = new TrieNode('/');//存储无意义字符串
public class TrieNode {
public char data;
public TrieNode[] children = new TrieNode[26];
public boolean isEndingChar;
public TrieNode(char data) {
this.data = data;
}
}
//往Trie树中插入一个数据
public void insert(char[] data) {
TrieNode node = root;
for(int i=0;i<data.length;i++) {
if(node.children[data[i]-'a']==null) {
node.children[data[i]-'a'] = new TrieNode(data[i]);
}
node = node.children[data[i]-'a'];
}
node.isEndingChar = true;
}
//在Trie树中查找一个数据
public boolean find(char[] data) {
TrieNode node = root;
for(int i=0;i<data.length;i++) {
if(node.children[data[i]-'a']==null) {
return false;//不存在
}
node = node.children[data[i]-'a'];
}
if(node.isEndingChar==false) {
return false;//不是完全匹配
}else {
return true;//完全匹配
}
}
}
public class TestTrieTree {
public static void main(String[] args) {
TrieTree tree = new TrieTree();
//how,hi,her,hello,so,see
tree.insert(new char[] {'h','o','w'});
tree.insert(new char[] {'h','i'});
tree.insert(new char[] {'h','e','r'});
tree.insert(new char[] {'h','e','l','l','o'});
tree.insert(new char[] {'s','o'});
tree.insert(new char[] {'s','e','e'});
System.out.println(tree.find(new char[] {'h','i'}));
System.out.println(tree.find(new char[] {'h','a'}));
}
}
运行结果
true
false