16----公式

news2024/9/30 23:27:36

本节我们来学习如何在markdown中打印公式

Markdown是一种轻量级标记语言，常用于撰写文档、博客和论坛帖子。虽然Markdown本身并不支持数学公式，但可以使用一些扩展来实现公式的显示。在支持公式扩展的 Markdown 解析器中，我们可以使用 Katex ,LaTeX,MathJax等语法在 Markdown 中使用公式。

不同的公式渲染器的语法定义也不同，一般分两种，行内公式和块公式。
行内公式一般前后各使用一个 $ 包裹;
块公式一般前后各使用两个 $ 包裹。

1. LaTeX:

LaTeX公式：LaTeX是一种专业的排版系统，广泛用于数学和科学领域。在Markdown中，可以使用LaTeX语法来编写数学公式。
例如，使用两个美元符号$$将公式包围起来，就可以将其显示为数学公式。

输入以下LaTeX语法：

$$
f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
$$

markdown解析后输出：
$\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

2. MathJax:

MathJax公式：MathJax是一个用于在网页中显示数学公式的JavaScript库。它支持多种数学公式的表示方式，并可以与Markdown配合使用。在Markdown中，可以使用MathJax语法来编写数学公式。例如，使用美元符号$将公式包围起来，就可以将其显示为数学公式。

输入以下MathJax语法：

$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

markdown解析后输出：

$\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

MathJax是一个功能强大的JavaScript引擎，可以将数学公式渲染为高质量的可交互式公式。它支持多种输入格式（如TeX和MathML），并可以在各种浏览器和操作系统上运行。MathJax可以自动检测和处理网页中的数学公式，并将其转换为可视化的形式。

3. Katex:

KaTeX是一个更轻量级的数学公式渲染引擎，专注于快速和高性能。它使用纯JavaScript实现，不依赖任何外部库，并且可以在客户端和服务器端都运行。KaTeX支持LaTeX语法，可以将LaTeX代码转换为可视化的数学公式。

输入以下Katex语法：

$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

markdown解析后输出：

$\frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

4. 使用HTML标签：

使用HTML标签：Markdown支持嵌入HTML标签，因此可以使用HTML标签来编写数学公式。例如，可以使用<sup>和<sub>标签来显示上标和下标，使用<sup>2</sup>表示平方。
例如：

H<sub>2</sub>O

这个公式将显示为：H₂O

5. 使用图片：

使用图片：如果Markdown编辑器或渲染器不支持公式扩展，可以将数学公式转换为图片，并将图片插入到Markdown中。有一些在线工具可以将LaTeX公式转换为图片，例如MathJax渲染器中的MathJax-node。
首先，将LaTeX公式写在$$之间，然后使用工具将其转换为图片，并将图片插入到Markdown中。例如：
这个公式将以图片形式显示在Markdown中。

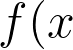![公式](https://latex.codecogs.com/png.latex?\dpi{300}&space;\bg_white&space;f(x)&space;=&space;\frac{1}{\sqrt{2\pi\sigma^2}}&space;e^{-\frac{(x-\mu)^2}{2\sigma^2}})

$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$