有时候在使用tilemap的时候,会希望在场景中添加更复杂的对象。
在2d-extras中,加入了预制件笔刷(Prefab Brush),可以将游戏物体预制体作为瓦片,来方便的在游戏场景中快速的绘制。可以自动适应游戏物体的位置。
预制件可以是3D对象、粒子效果或者动画对象。
一般移动方法移动游戏物体,不能够精确到位置;使用Prefab Brush,可以把3D物体定义为Tiles,将其刷到场景中。然后创建一个tilemap,在tilemap下方选择笔刷,然后使用笔刷工具即可实现快速刷预制体的效果。
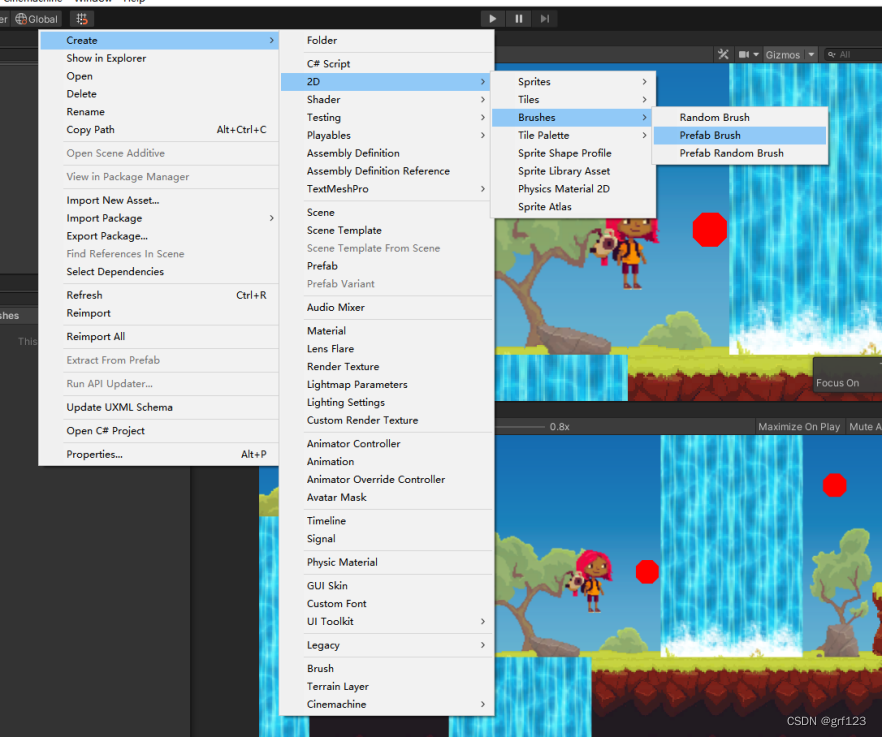
创建步骤:Create->Prefab Brush,然后选取刚创建的预制体。
这里有一个B站搬运的视频:
【圈毛中英自翻】Unity官方 Tilemap: Prefab Brush 1080p_哔哩哔哩_bilibili
这个预制体笔刷,可以方便的将3D对象整合到2D游戏场景中。实例中旋转的宝石就是一个很好的例子。利用简单的旋转就能实现仿真的效果。
这里提到了在3D场景中使用预制体笔刷:
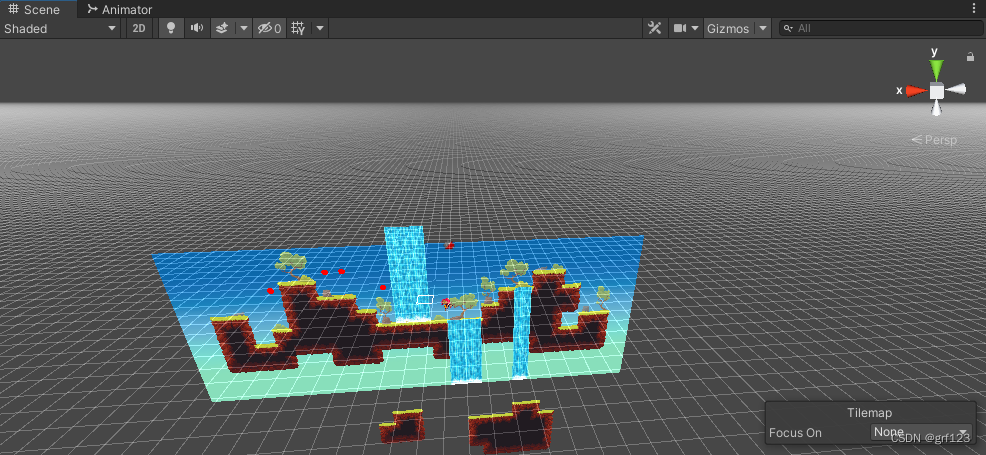
如果将场景切换为3D,在2D场景中创建的tilemap在3D场景中默认显示是竖直的,可以修改Grid的属性Cell Swizzle:默认为XYZ

要使用3D俯视图,修改为XZY。
这个时候可以看到,我们这个Tilemap就是在3D场景中平铺的这个了。
修改了Grid的同时,也要修改Tilemap中的Orientation为XZ。
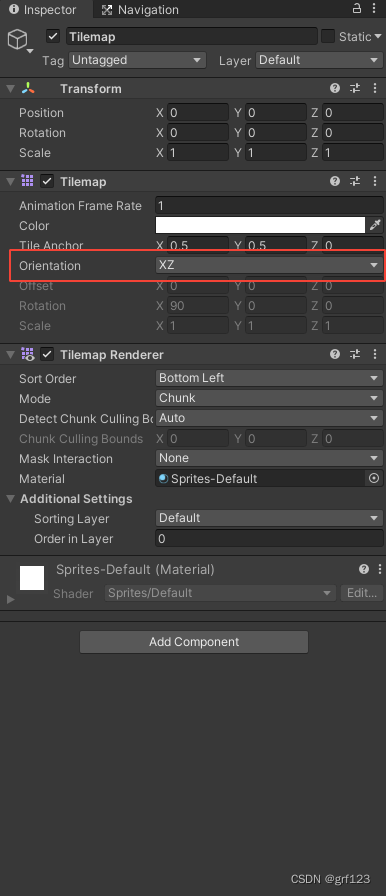
这样,tilemap的效果看起来就很好啦。






![[国产MCU]-W801开发实例-GPIO输入与中断](https://img-blog.csdnimg.cn/11706f63104d4d5cbcd8ed76a4bf459a.png#pic_center)