论文：Factor Fields: A Unified Framework for Neural Fields and Beyond
文章：https://arxiv.org/abs/2302.01226
项目：https://apchenstu.github.io/FactorFields/

---

---

摘要

Factor Fields，一个新的框架来建模和表示信号：将信号分解为Factor 的乘积，每个Factor 由经典场或神经场表示，它对转换后的输入坐标进行操作。这种分解产生了一个统一的框架，该框架容纳了几种最近的信号表示，包括NeRF、Plenoxels、EG3D、Instant-NGP和TensoRF。此外，模型允许创建强大的新信号表示，如“字典场”（DiF）。快速重建方法中，DiF方法提高了近似(approximation)质量、紧凑性和训练时间。

实验表明，Factor Fields 在二维图像回归任务上获得了更好的图像逼近质量，在重建 SDF (符号距离场) 时具有更高的几何质量， 在NeRF 重建任务上具有更高的紧凑性。此外， DiF通过在训练过程中共享信号基，能够泛化到不可见的图像/三维场景，这极大地有利于了使用案例，如稀疏观测的图像回归和 few-shot 辐射场重建等。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、前言

有效地表示多维数字内容——如2D图像或3D几何图形和外观——对于计算机图形学和视觉应用程序是至关重要的。这些数字信号传统上被离散地表示为 pixels,
voxels, textures, 或 polygons。近年来，[36,51,37,10,49]在开发先进的神经表示法方面取得了重大进展，建模精度和效率方面优于传统的表示方法。

Factor Fields统一了多维信号的神经表示：通过将一个信号分解为多个Factor Fields（f₁，……，f_N），通过选择适当的坐标变换（γ₁，……，γ_N），如图1所示。Factor Fields（ 在坐标变换信号域的任何空间位置）解码多通道特征，然后通过学习的投影函数（例如，MLP）从 factor 的点乘回归目标信号。

模型适应了大多数神经表征，它们中的许多可以在我们的框架中通过域变换表示为一个单一因素——例如，MLP网络作为NeRF中具有位置编码转换的一个factor[36]，在Instant-NGP[37]中哈希变换的表格编码作为一个因子；在DVGO [51]和Plenoxels[61] 中具备一致性（identity）变换的特征网格。TensoRF [10]引入了一种基于张量因子分解的表示，它可以看作是两个向量-矩阵 或三个具有轴对齐正交的二维和一维投影的CANDECOMP-PARAFAC对数分解因子的表示。

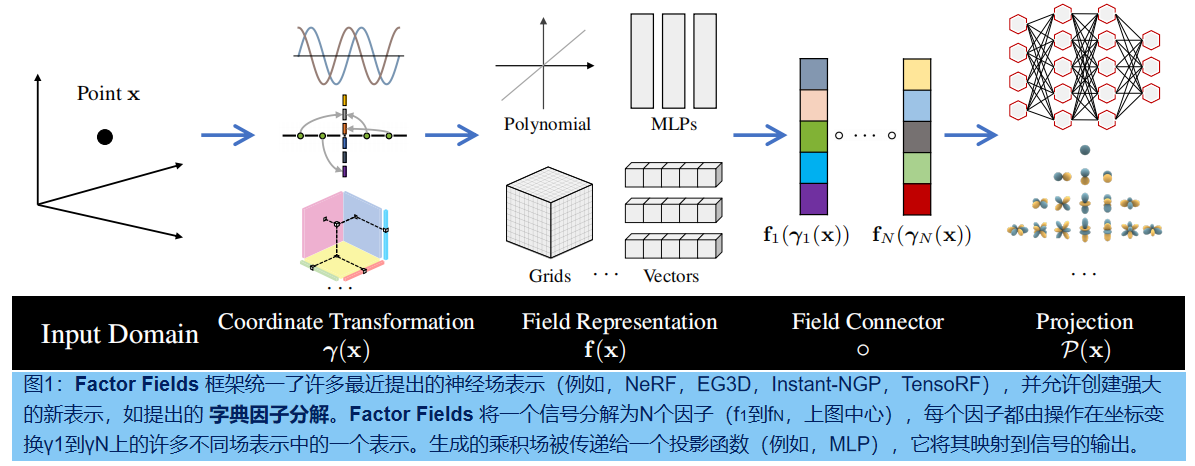
这促使我们通过一个单一的统一框架来概括以前的经典神经表示，使以前的神经域和转换功能能够简单而灵活地组合，从而产生新的表示设计。例如在字典领域（DiF），一个two-factor 表示由 ：（1）一个具有周期变换的 基函数因子basis functions，以建模跨整个信号域的模式的共性（2）一个用一致性变换的 系数场因子coefficient functions来表示信号中的局部空间变化特征。这两个因素的结合允许有效地表示信号的全局和局部属性。请注意，以前的大多数单因素表示可以视为只使用其中一个函数——要么是基函数，如NeRF和Instant-NGP，要么是系数函数，如DVGO和Plenoxels。在DiF中，联合建模两个因素（基和系数）可以获得比以前的方法如inist-NGP更好的质量，并能够实现紧凑和快速的重建，正如我们在各种下游任务中所演示的那样。

由于DiF是通用 Factor Fields 家族的一员，我们对基/系数函数和基变换的选择进行了一组丰富的消融实验。与Instant-NGP相比，我们的方法具有更好的重建和渲染质量，同时有效地将SDF和辐射场重建的模型参数总数（容量）减半，证明了其优越的精度和效率。此外，与最近纯粹为每个场景优化而设计的神经表示相比，我们的分解表示框架能够学习不同场景中的基函数 (多个二维图像或三维辐射场中学习跨场景基)，从而得到信号表示，从而改进稀疏观测的重建结果，如在few shot NeRF重建设置中。

二、Factor Fields

我们试图在D维域上紧凑地表示一个连续的Q维信号s： R^D→R^Q。我们假设信号不是随机的，而是结构化的，因此在同一信号内（空间和不同的尺度）以及不同的信号之间共享相似的特征。接下来，我们从标准基开始，逐步开发我们的Factor Fields 模型。

2.1.字典场（DiF）

首先考虑一个一维信号=(x)：R^D→R。利用基展开，我们将s (x)分解为一组系数c=（c₁，…，c_K)^⊤ 和基函数b (x) = (b₁(x)，…，b_K（x)^⊤ 。其中, c_k∈R ，b_k: R^D→R：

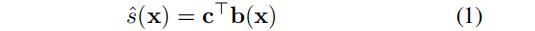
注意，s(x)表示为真实的信号，将 $\hat{s}$(x) 表示为它的近似值。

使用全局的一组基函数来表示信号s (x)是效率低下的，因为信息不能在空间上共享。因此，我们推广了上述公式，通过 (i) 利用空间变化系数场c (x) =（c₁₍x)，…，c_K(x))^⊤ 与 c_k: R^D→R和 （ii） 通过坐标变换函数γ: R ^D→R^B 变换基函数的坐标：

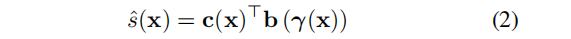
当选择γ作为周期函数时，公式允许我们在多个空间位置，以及选择在多个不同的尺度上， 应用相同的基，同时改变系数c，如图2所示。注意，一般B不需要匹配D，因此基函数的域也相应地变化： b_k： R^B→R。进一步，我们设置c (x) = c和γ(x) = x，得到等式(1)的特殊情况。

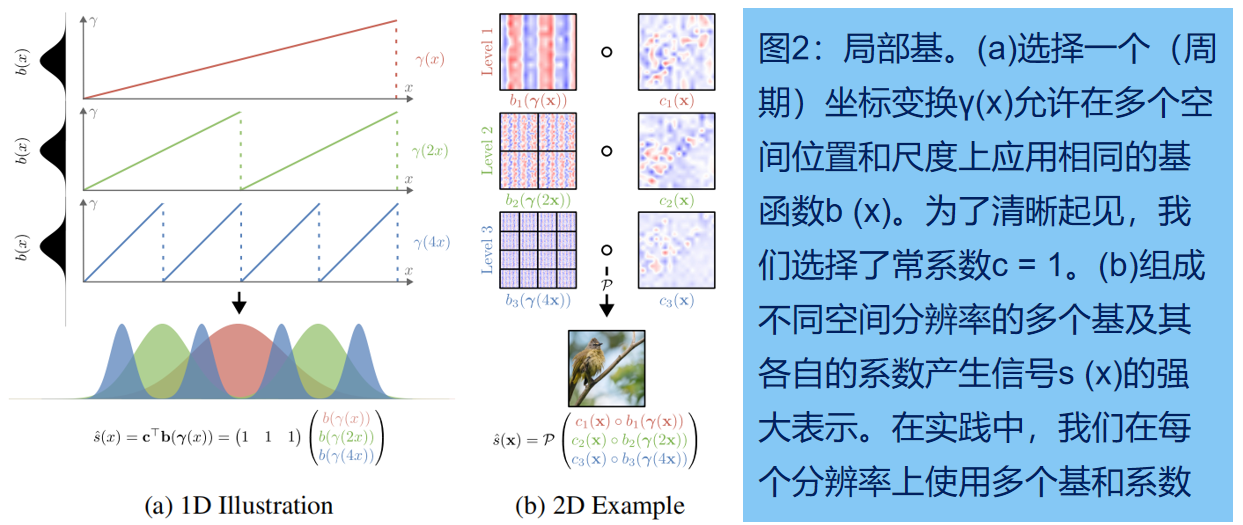
以上只考虑了一个一维信号s (x)。然而，许多信号具有多个维度（例如，RGB图像为3，辐射场为4）。我们通过引入一个投影函数P： R^K→R^Q，并将内积（下面用◦表示）替换为元素乘法，来将我们的模型推广到Q维信号f(x)：

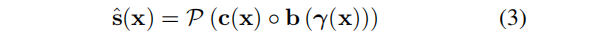
等式(3)即Dictionary Field（DiF）。与等式(2)中的标量积 c^⊤b 相比，c◦b 的输出是一个 包括单个系数和基 点乘的 K维向量，作为投影函数P的输入。投影函数P本身可以是线性或非线性的。在线性情况下，P (x) = Ax，A∈R^Q×K。此外，对于Q = 1和A =（1，……，1）作为公式(2)的特殊例。2.3节所述，从2D图像观测中重建三维辐射场时，投影算子P也可以用来建模体渲染操作。

2.2.Factor Fields f_i

为了涵盖两个以上的 factor，推广等式(3)到 full Factor Fields 框架，通过将系数c (x)和基b (x)替换为一组 Factor Fields：{f_i (x)}^N_i=1

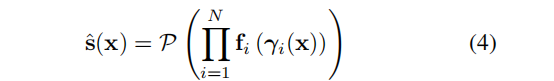
Π 表示一系列 factor 的元素级乘积。该一般形式中，每个factor f_i：R ^Fi→R^K，都可以配备自己的坐标变换 γ_i： R^D→R^Fi。通过设置f₁(x) = c (x)、γ₁(x) = x、f₂(x) = b (x)和γ~2(x) = γ(x)与N = 2，等式(3)作为等式(4)中的一个特例。

{γ_i}是确定性函数，而P和{f_i}是参数映射（例如，多项式，多层感知器或三维特征网格）， 其参数θ既可以对单个信号进行优化，也可以对多个信号进行联合优化。当对多个信号进行联合优化时，我们在信号之间共享投影函数和 basis factors 的参数（但不是系数factors 的参数）。为了对 factor fields f_i：R^Fi→R^K 建模，我们考虑各种不同的表示（多项式、mlp、二维和三维特征网格和一维特征向量）。mlp已被提出作为 Occupancy Networks[35]、DeepSDF [40]和NeRF中的信号表示。虽然mlp在紧凑性方面表现出色，并引入了有用的平滑偏置，但验证速度慢，消耗了训练和推理时间。

为了加速，DVGO [51]提出了一个针对辐射场的三维体素网格表示。虽然体素网格可以快速地进行优化，但它们显著地增加了内存，并且不容易扩展到更高的维度。为了更好地捕获信号的稀疏性，Inistant NGP[37]提出了一个结合一维特征向量的哈希函数，而不是密集的体素网格，TensoRF [10]将信号分解为矩阵和向量的积。 factor fields 允许这几种表示来建模任意 factor f_i。

2.3. 坐标变换 γ_i

每个factor fields f_i 的输入的坐标，通过坐标变换函数 γ_i：R^D→R^Fi 进行变换:

1.系数

factor fields f_i 表示系数时，使用恒等映射 γ_i(x) = x来进行相应的坐标变换，因为系数在信号域上可以自由变换

2.局部基 （Local Basis）

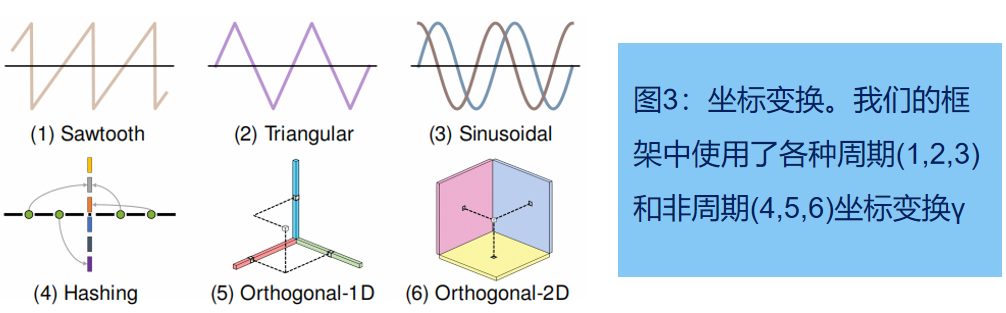
坐标变换γ_i可在多个位置应用相同的基函数 f_i，如图2所示。具体可使用sawtooth, triangular、正弦（如NeRF中）、哈希（如Instant NGP）和正交（如TensoRF[10]中）变换，见图3。

3.多尺度基

坐标变换γ_i 还允许在不同的信号空间分辨率下应用相同的基 f_i ，通过用不同频率的（或周不同期）的变换来变换坐标 x，如图2所示。这是至关重要的，因为信号通常同时携带高频和低频，可利用我们的全频谱的基表示来建模信号的细节以及平滑的信号组件。

具体来说，我们用一组多尺度（视场）基函数对目标信号进行建模。我们将基分成 L 级，每个级别都覆盖不同的尺度。设 [u，v] 表示信号沿一维方向的边界框。相应的尺度由 (v−u) / f_l 计算，其中 f_l 为L级的频率。大尺度基（如，level 1）具有低频并且覆盖目标信号的大区域，而小尺度基（如，level L）具有覆盖目标信号的小区域的大频率 f_L。

我们通过将场景坐标x与每层频率 f_l 相乘来实现多尺度表示（PR），然后将其输入坐标变换函数 γ_i，然后将结果拼接到不同尺度的 l = 1，…，L：

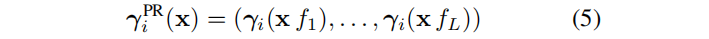
其中，γ_i 是图3中的任何一个坐标变换，而 γ_PR 是多尺度表示的最终坐标变换。最终目标信号s (x)被分解为空间变化系数图和由重复的局部基函数组成的多层次基图的乘积。

2.4 投影P

为了表示多维信号，我们引入了一个投影函数P： R^K→R^Q，它从K维的 Hadamard乘积 Π_if_i 映射到Q维目标信号。我们区分了两种情况：从目标信号的直接观测可用的情况（例如，RGB图像的像素），以及间接观测是目标信号的投影的情况（例如，从辐射场渲染的像素）

直接观测：最简单的情况下，投影函数实现了一个可学习的线性映射P (x) = Ax，参数A∈R^Q×K，将K维Hadamard乘积 Π_if_i 映射到Q维信号。实验的默认设置：P用一个浅层的非线性多层感知器（MLP）表示，模型更加灵活。

间接观察：有时，只能获得对信号的间接观察。如NeRF只需观察二维图像，而不是4D信号（密度和亮度）。在这种情况下，扩展P还包括可微体积渲染过程。具体说，首先应用MLP来映射视图方向d∈R³，连乘特征 Π_if_i 在特定位置x∈R³ ，到颜色值c∈R³ 和体积密度σ∈R。然后利用NeRF中的离散化积分累计函数：

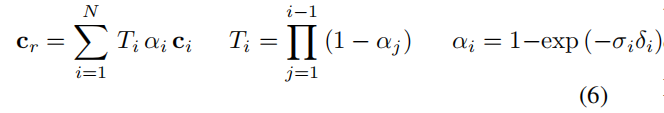
2.5 空间收缩

通过对x应用一个简单的空间收缩函数，我们将输入坐标x∈R^D 归一化到[0,1]，传递给坐标变换γ_i (x)。区分两种设置：

对于边界为[u，v]（u，v∈R^D）的D维有界信号，利用线性映射将坐标归一化到范围[0,1]，如公式7；对于无界信号（例如，一个室外辐射场），我们采用Mip-NeRF360的[3]空间收缩函数，如公式8

2.6 优化

优化目标（Ψ(θ)是模型参数的一个正则化）：

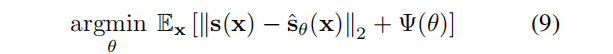
稀疏正则化。对稀疏系数使用L0范数是可取的，但很难优化。相反，我们使用了一种简单策略：以概率µ随机删除模型的K个特征的一个子集（设置为零），来规范我们的目标。这迫使信号在每次迭代中以特征的随机组合来表示，鼓励稀疏性和防止特征的共同适应。我们使用一个随机二进制向量实现这个 dropout 正则化，通过元素乘积：◦Π_if_i 。

初始化：实验使用离散余弦变换（DCT）初始化基（basis factors），同时随机初始化系数 factor 和投影MLP的参数（消融研究表3a到表3e）。

多信号：对多个信号进行联合优化时，在不同信号之间共享投影函数和基（basis factors）的参数（但不是系数因子的参数）。第4.3节实验证明，在鼓励稀疏系数的同时，跨不同的信号共享基可以提高泛化效果，并能够从稀疏观测中进行重建。

三、factor fields 作为一个通用的框架

受经典的因子分解和学习技术的启发，如稀疏编码[57,59,18]和主成分分析（PCA）[46,33]，我们提出了一种新的基于神经因子分解的神经表示框架。factor fields 统一了许多最近的神经表示，并使 factor fields 家族中的新模型能够实例化。

3.1.Occupancy Networks, IMNet 和 DeepSDF

这几种方法，隐式地将曲面表示为MLP分类器的连续决策边界，或通过回归一个有符号的距离值。普通的MLP表示提供了一个连续的隐式3D映射，允许在任何分辨率下提取3D网格。当使用单因子（即N = 1）和γ1(x) = x，fx(x(x)=x，P (x) = MLP (x)，因此 $\hat{s}$(x)=MLP(x)。虽然这种表示能够生成高质量的网格，但由于mlp的隐式平滑偏差，它无法建模高频信号，如图像

3.2 NeRF

提出通过一组傅里叶正弦函数编码空间坐标，用傅里叶空间中的MLP来表示辐射场。如： γ₁(x) =（sin(xf₁), cos(xf₁), …,sin(xf_L), cos(xf_L)）、f₁(x) = x和P (x) = MLP (x)。在这里，坐标变换γ₁(x)是一个正弦映射，如图(3)，可以实现高频转换。

3.3 Plenoxels 体素点云

使用稀疏体素网格来表示三维场景，无需神经网络进行直接优化，能够快速训练。factor field 设置N = 1、γ₁(x) = x、f₁(x) =3D-Grid(x)，密度场：P (x) = x， 辐射场：P(x)=SH(x)（球谐波）相对应。相关工作中，DVGO [51]用密集的网格代替了稀疏的三维网格，并使用一个微小的MLP作为投影函数P。密集的网格建模很简单，并会导致快速的特征查询，但它需要很高的空间分辨率（因此也需要很大的内存）来表示细节。

3.4 ConvONet and EG3D

对有界场景中的空间点应用正交坐标变换，使用三平面表示来建模三维场景，然后将每个点表示为从一组二维特征映射中查询的特征的连接。这种表示使用2D卷积来聚合3D特性，大大减少了内存占用。

factor field 设置：N = 1，γ₁(x) =Orthogonal-2D(x)，f₁(x) = 2D-Maps (x) 和P (x) = MLP (x)。

然而，虽然轴对齐的转换允许沿轴进行降维和特征共享，但由于该表示的轴对齐偏差（ axis-aligned bias），处理复杂的结构可能具有挑战性。

3.5 Instant-NGP

Instist-NGP 利用多 layer 的哈希网格，通过将空间位置 hash 到一维特征向量，有效地建模目标信号的内部特征。使用N = 1，γ₁(x) =hash (x)，f₁(x) =Vectors(x)和P (x) = MLP (x)，L=16。然而，多层哈希映射会导致 fine scales 的密集冲突。一对多映射迫使模型将其 capacity bias 分布到密集观测区域，而观测较少的区域产生噪声。同期工作VQAD [52]引入了一个分层的向量量化自动解码器（VQ-AD）表示，它学习一个索引表作为坐标转换函数，从而允许更高的压缩率。

3.6 TensoRF

TensoRF将辐射场分解为向量和矩阵（TensoRF-VM）或多个向量（TensoRF-CP）的乘积，在低内存占用下实现高效的特征查询。这个设置实例化了Factor Fields：

N = 2, γ₁(x) = Orthogonal-1D(x), f₁(x) = Vectors(x), γ₂(x) = Orthogonal-2D(x), f₂(x) = 2D-Maps(x) : VM 分解
N = 3, γ_i(x) = Orthogonal-1D(x), f_i(x) = Vectors(x) ：CP 分解

TensoRF同时使用SH和MLP模型来投影p。与ConvONet和EG3D类似，坐标由于使用正交变换函数，TensoRF对坐标系的方向很敏感。注意，除TensoRF 外，上述所有表示都使用单 factor field 分解信号，即N = 1。表3a到表3d说明了，使用多 factor field （即N > 1）提供更强的模型能力。

3.7 ArXiv Preprints

神经表征学习领域正在快速发展，许多新的表征最近已经在ArXiv上预发表。相关工作有：相位嵌入场（PREF）提出代表一个目标信号的相位体，然后将它们转换成空间域反快速傅里叶变换（iFFT）紧凑表示和高效的场景编辑。该方法与DVGO有相似的思想，并用iFFT函数扩展了公式中的投影函数P。Tensor4D[48]将三平面表示，通过使用三平面 factor field 和具有3个正交坐标变换的索引平面特征 (即Orthogonal-2D(x) = (xy, xt, yt), Orthogonal-2D(x) = (xz, xt, zt), Orthogonal-2D(x) = (yz, yt, zt)）扩展到四维人体重建。

D-TensoRF [20]使用矩阵矩阵分解重建动态场景，类似于TensoRF的VM分解，但替换γ₁(x) =Orthogonal-1D(x)和f₁(x) =Vector (x)与γ₁(x) =Orthogonal-2D(x)和f1(x) =Vector(x)。Factor Fields 框架使用N=1，γ₁ sinusoidal (x)，f₁(x)= 2D-Maps(x)，和P(x)=(x)MLP(x)来进行2D表示。

3.8 Dictionary Field (DiF)

除以上表示，Factor Fields 还能具有理想属性的新表示，如公式 (3)。DiF提供了隐式正则化，紧致性和快速优化，可推广到多个信号。核心思想是将目标信号分解为两个域：一个全局域（即基）和一个局部域（即系数）。全局域促进在空间位置和尺度以及信号之间共享的结构化信号特征，而局部域允许空间变化的内容。

DiF将目标信号分解为系数域 f₁(x) = c (x)和基函数 f₂(x) = b (x)，主要根据各自的坐标变换而变化。我们为 c(x) 选择恒等式映射 γ₁(x) = x，为 b(x) 选择周期坐标变换 γ₂(x)，见图3上。

作为两个factor fields f₁ 和f₂ 的表示，我们可以选择图1（左下角）中所示的任何一个。为便于比较，实验中使用 sawtooth 函数作为基坐标变换γ₂ ，并使用均匀网格 (uniform grids) 作为系数场 f₁ 和基函数f₂ 的表示。

四、实验

4.1 实施细节

PyTorch框架，单个RTX 6000 GPU上使用Adam优化器上进行评估，学习率为0.02。

我们使用频率（线性增加）f_l ∈ [2., 3.2, 4.4, 5.6, 6.8, 8.] 以及L = 6 levels 来实例化DiF，以及特征通道 K=[4,4,4,2,2,2]^⊤·2η，其中η控制特征通道的数量。采用 η = 3进行2D实验，使用η= 0进行3D实验。模型参数θ分布在3个组成模型上：系数 θ_c、基θ_b 和投影函数 θ_P。每个模型大小根据所选的表示而不同。

实验模型设置为“DiF-Grid”，它使用可学习的张量网格:P (x) = MLP (x)和γ(x) =Sawtooth(x)，其中Sawtooth(x) = x mod 1.0。在DiF-Grid设置中，可优化参数的总数主要由系数和基网格的分辨率 M^l_c、M^l_b 决定：

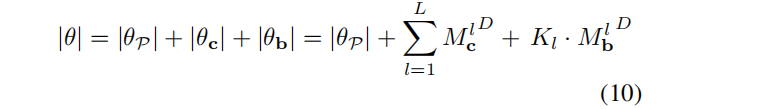
使用线性增加的分辨率 M^l_b ∈[32,128]^T·min(v−u)/1024 来实现基网格，其间隔为[32,128]，场景边界[u，v]。我们在L个 level 上使用相同的网格分辨率 M^l_c ，以提高查询效率并降低每个信号的内存占用。

DiF的不同模型变体被标记为“DiF-xx”，其中“xx”表示与默认设置“DiF-Grid”的差异。例如，“-MLP-B”指的是使用MLP基的表示，而“SL”代表 single level。

4.2 Single Signals

我们首先评估了我们的 DiFGrid 表示在各种多维信号上的准确性和效率，并将其与最近的几种神经信号表示进行了比较。为了实现这一目标，我们考虑了三个常用的评估神经表征的基准任务：二维图像回归、三维有符号距离场（SDF）重建和辐射场重建/新视图合成。我们评估了每种方法近似高频模式的能力，插值质量，紧凑性，以及对歧义和稀疏观测的鲁棒性。

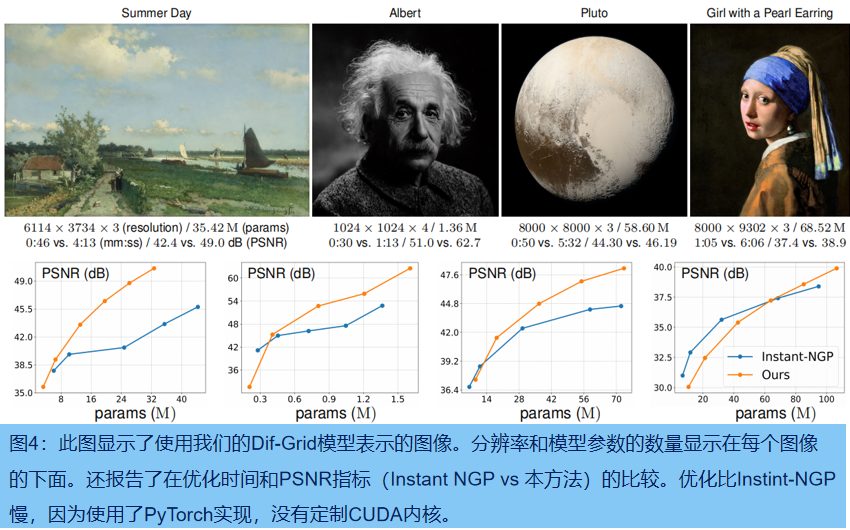
二维图像回归：在这个任务中，我们直接从像素坐标中回归RGB像素的颜色。我们评估我们的dif-网格拟合四个复杂的高分辨率图像，像素总数从4M 到213M。图4了显示重建图像与同样大小的模型，如InstantNGP，达到更高的PSNR。（Instant NGP高度优化了基于CUDA的框架，实现了更快的优化）。

符号距离场 SDF重建：

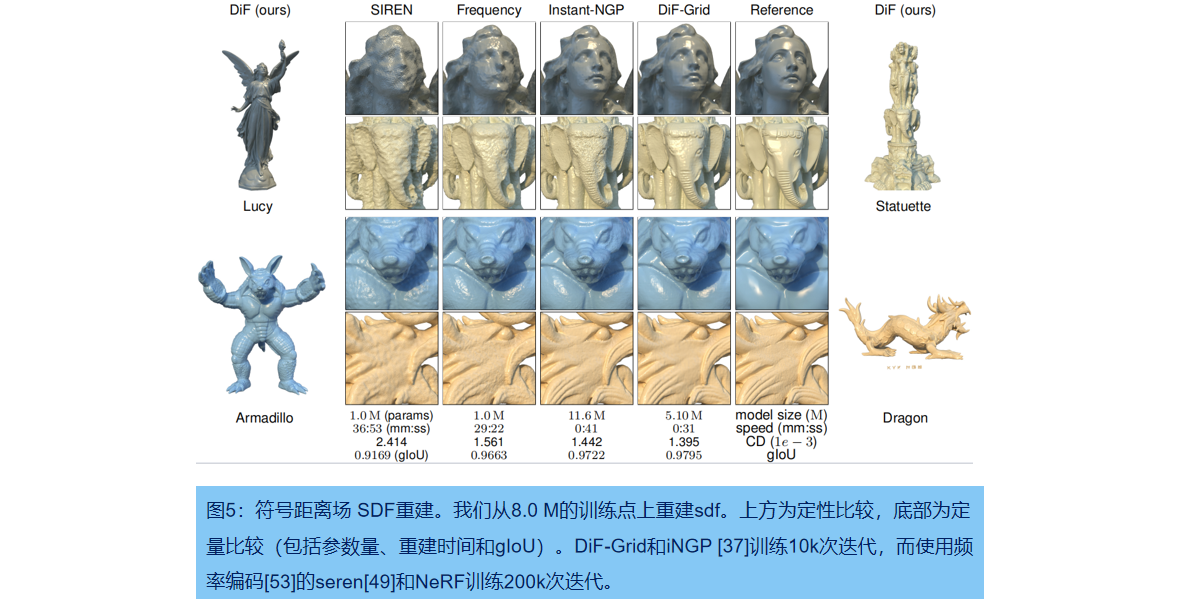
SDF作为一种经典的几何表示法，描述了一组连续的 iso 曲面。与最先进的神经表示进行比较，包括傅里叶特征网络[53]、SIREN [49]和 Instant-NGP[37]。对所有方法使用相同的训练方式，通过从目标 mesh 中预采样8M的SDF点进行训练，其中80%点靠近表面，其余20%点均匀分布在单位体积内。根据Instiast-NGP，我们随机抽取16 M点进行评估，并基于SDF符号计算几何IOU度量（X是待评估的点集）：

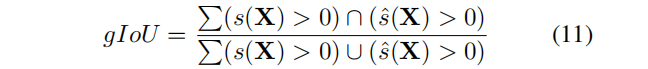
图5为定量和定性比较：本方法有高频几何细节，并包含更少的光滑表面的噪声，最高的gIoU值上，最快的重建速度，Instant-NGP使用的一半的参数。

辐射场重建：

辐射场重建的目的是从多视图RGB图像中，恢复每个体素点的密度和亮度。许多编码函数和高级表示方法被提出，显著提高了重构速度和质量，如稀疏体素网格[16]、哈希表[37]和张量分解[10]。

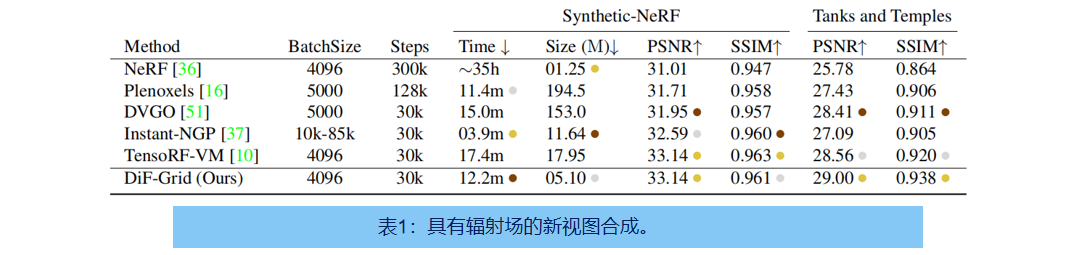
表1定量比较了Dif-Grid与几种最先进的快速辐射场重建方法（Plenoxel [16], DVGO [51], Instant-NGP [37]
and TensoRF-VM）在合成[36]以及真实场景（坦克和寺庙物体）[24]上的应用。

总体上，我们的模型在三个具基准测试任务上，都有最先进的结果。基线大多是 single-factor 的，利用局部场（如DVGO和 Plenoxels）或全局场（如即时-NGP）。DiF模型是一种 two-factor 方法，结合了局部系数和全局基场，从而产生更好的重建质量和记忆效率。

4.3 泛化

最近的先进神经表征，（如NeRF, SIREN, ACORN, Plenoxels, Instant-NGP and TensoRF ）分别优化每个信号，缺乏联合建模多个信号或从多个信号中学习有用的先验的能力。相比之下，DiF表示不仅能精确和高效重建每个信号（如第4.2节），还可通过简单地跨信号实例共享基场来应用于跨信号的泛化。

我们通过对部分像素观测和少镜头辐射场重建的图像回归实验来评估基础共享的好处。在这些实验中，我们采用DiF MLP-B（即表3d中的(5)）作为我们的DiF表示，而不是DiF Grid，其中我们使用张量网格来建模系数，使用6个微小的mlp（两层各有32个神经元）来建模基。DiF-MLP-B在泛化设置中的表现优于DiF-Grid，这是由于mlp具有较强的归纳平滑偏差。

从稀疏观测结果中回归得到图像：
本实验侧重于在优化过程中只使用部分像素的场景。在没有额外的先验的情况下，由于稀疏观测和有限的归纳偏差，单信号优化在此设置中很容易过拟合，因此无法恢复看不见的像素。

我们使用DiF-MLP-B模型来学习数据先验，通过对来自FFHQ数据集[21]的800张面部图像进行预训练，同时共享MLP基和投影函数参数。最后的图像重建任务是通过优化每个新的测试图像的系数网格来进行的。

图7展示了三种使用不同mask 的面部图像回归结果。即使没有预训练和其他图像先验，DiF-MLP-B也能够在一定程度上捕获被优化的同一图像中的结构信息；如眼睛区域所示，模型可以从右眼学习瞳孔形状，并通过在共享基函数中重用学习到的结构回归左眼（在训练中mask）

Few-Shot 辐射场重建

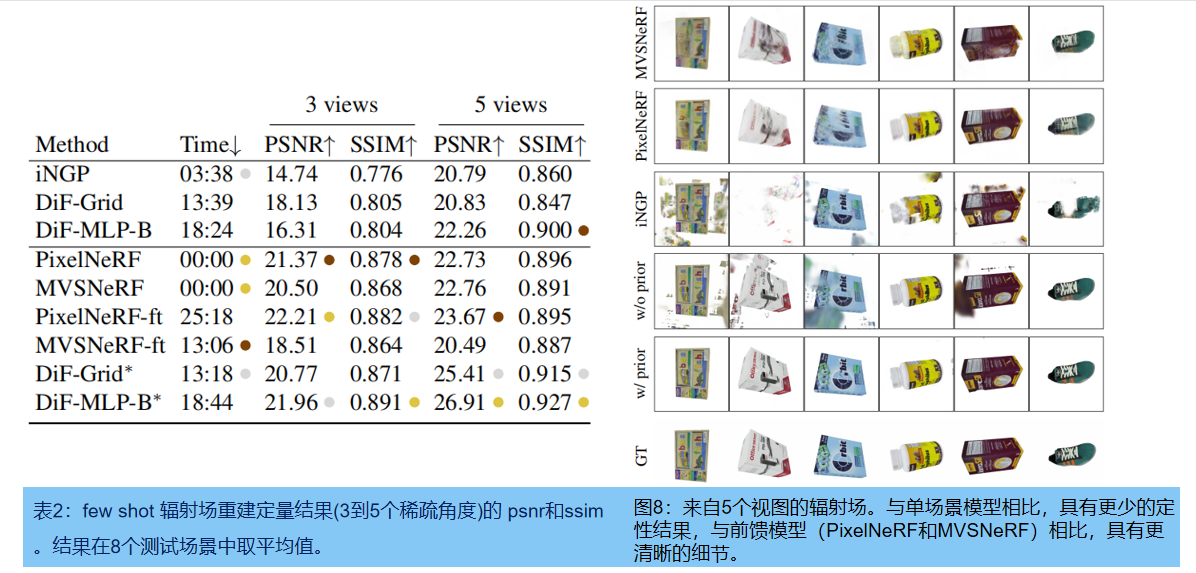
以前的工作通过在每个场景优化中施加稀疏性假设[38,22]或从数据集训练前馈网络[61,12,26]来解决这个问题。我们考虑每个场景的3个和5个输入视图，在优化任务中利用我们的DiF模型的预先训练的基场中的数据先验。值得注意的是，视图是在四分之一的球体中选择的，因此视图之间的重叠区域相当有限。

具体来说，我们首先在100个谷歌扫描对象场景[15，每个场景250个视图]上训练DiF模型，其中。在跨场景训练中，我们保持每场景100个系数，并共享基c和投影函数P。跨场景训练后，我们使用预训练的系数场的平均值作为初始化，同时固定预训练的函数（c和P），并对few shot 观测的新场景的系数场进行微调。在这个实验中，我们比较了DiF-MLP-B 和DiF-Grid 和没有预训练的结果。

我们还与Instant NGP和其他 few shot 方法（PixelNeRF [61]和MVSNeRF [11]）用相同训练集训练，并使用相同的3或5个视图进行测试。如表2和图8所示，MLP的预训练DiF为 few shot 重建提供了强大的正则化，比没有数据先验的单场景优化方法和之前使用预训练网络的方法具有更少的伪影和更好的重建质量。没有数据先验的单场景优化方法，对输入图像过拟合，导致许多异常值。MVSNeRF和PixelNeRF实现了合理的重建，因为它们学习了前馈预测，避免了每个场景的优化。然而，它们却遭受着模糊的假象。

4.4 Factor Fields设计选择的影响

这里对Factor Fields 框架的四个主要组件进行了效率、紧凑性、重建质量和通用性方面的评估：因子数N、级别数L、坐标转换函数γ_i、场表示f_i 和场连接器 ◦ 。

对于2d图像回归任务，我们使用相同的模型设置在4.2节和测试256个高保真图像的分辨率为1024×1024从DIV2K数据集[1]。

Factor 因子数量

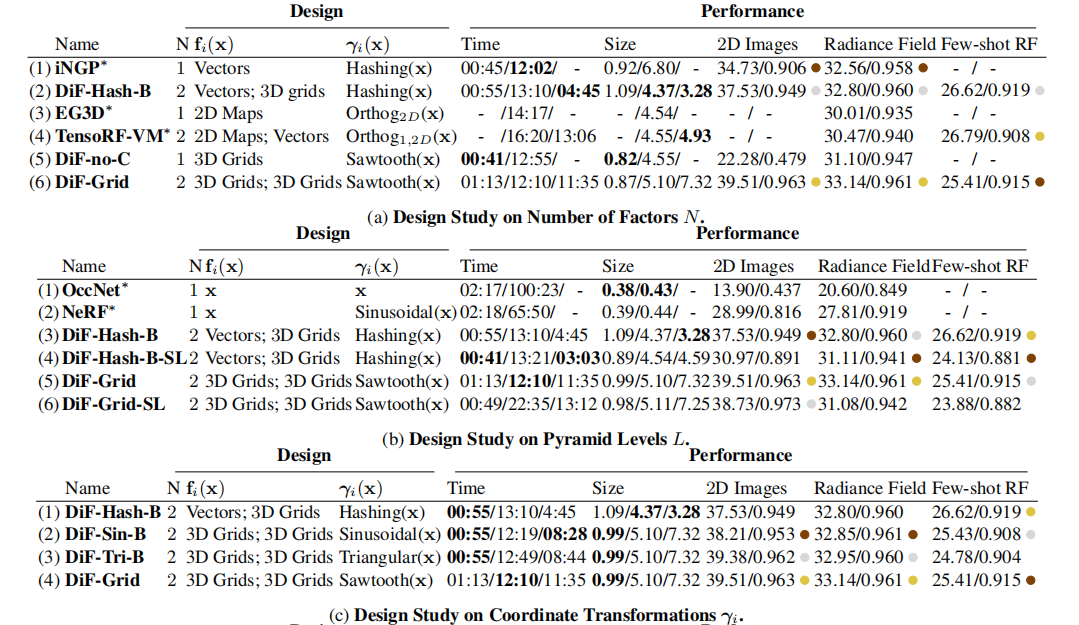
如公式(4)中，factors 数 N是指用于表示目标信号的factors 数量。我们在表3a中展示了单因子模型（1、3、5）和双因子模型（2、4、6）。与模型(1) iNGP(3) EG3D和(5) DiF-no-C相比，模型 (2) DiF-Hash-B、(4) TensoRF-VM和(6)DiF-Grid 分别使用与(1)(3)(5)相同的 Factor ，但扩展到双 Factor 模型，在图像回归和3D辐射场重建任务中提高了3 dB和0.35 dB PSNR，同时增加了训练时间（∼10%）和模型尺寸（∼5%）。

虽然计算开销很小，但因子间的乘法使两个因子域可以相互调节彼此的特征编码，并更灵活地联合表示整个信号，缓解了Instint-NGP中的特征冲突问题和其他单因子模型的相关问题。此外，如表1所示，多因子建模（如N >= 2）能够提供更紧凑的建模，它还允许通过跨实例部分共享场来进行泛化，例如在few shot 重建任务中的跨场景辐射场建模。

Level 数量 L:

DiF模型采用了多层的变换，来实现金字塔式的基场，类似于在NeRF [36]中使用的一组正弦位置编码函数。我们将多级别模型（包括DiF和NeRF）与表3b中只使用单一转换级别的简化单级版本进行了比较。请注意，Occupancy Networks（OccNet，行(1)）不利用位置编码，可以被视为NeRF的single level 版本（行(2)），而具有多级正弦编码函数（NeRF）的模型在2D图像和三维重建任务中都可以提高约10 dB PSNR的性能。

坐标变换 γ_i：

表3c：使用DiF表示来计算四个坐标变换函数（正弦形、三角形、哈希形和锯齿），变换曲线如图3。一般来说，与随机哈希函数相比，周期变换函数（2,3,4）允许通过重复模式共享空间相干的信息，其中相邻的点可以在基域中共享空间相邻的特征，从而保持局部连通性。我们观察到，周期基在建模密集信号（如二维图像）方面取得了明显更好的性能。对于稀疏信号，如三维辐射场，所有四个转换函数都实现了与以前最先进的快速辐射场重建方法相同的高重建质量

场的表示 f_i：

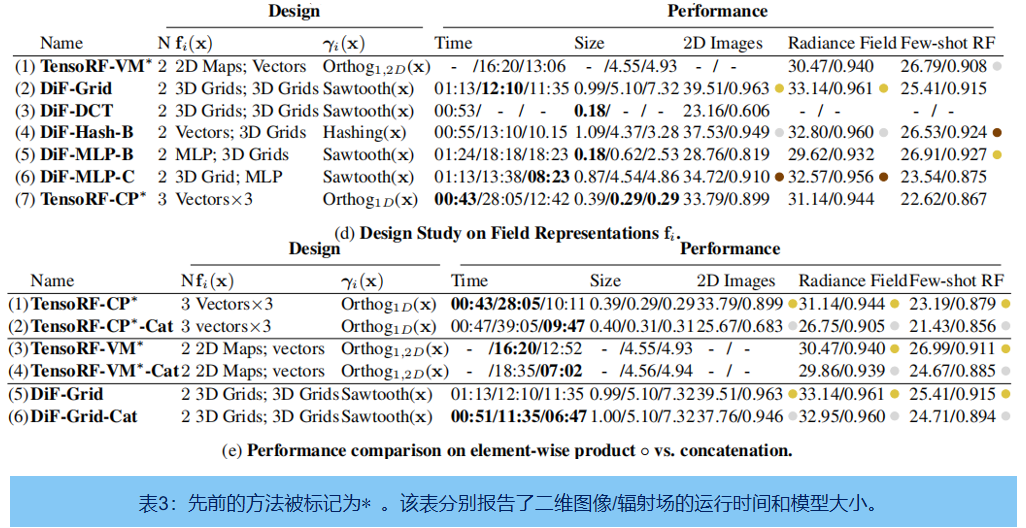
表3d比较了DiF模型中 factor 的各种功能，包括mlp、向量、2D Map和3D Grid。离散特征网格函数（3D网格、2D映射和向量）通常比MLP函数导致更快的重建（例如，DiF-Grid比DiF-MLP-BandDiF-MLP-C快）。虽然所有的变量都可以为单信号优化提供合理的重建质量，但我们的双网格表示在图像回归和单场景辐射场重建任务上取得了最好的性能。另一方面，few shot 辐射场重建的任务得益于施加更强的正则化的基函数。因此，与其他变体相比，具有更强的归纳偏差的表征（例如，TensoRF-VM中的 Vectors 和DiF-MLP-B中的MLPs）会导致更好的重建质量。

现的连接器 ◦：

我们的Factor Fields 和DiF模型的另一个关键设计是， 采用元素级相乘来连接多个 Factor 。在表3e中，我们比较了元素级乘法与三个模型直接拼接的性能。在重建质量方面，元素级乘法始终优于拼接操作。

五、环境安装与使用

1.安装环境

克隆好代码，然后按以下步骤安装依赖

conda create -n FactorFields python=3.9
conda activate FactorFields
conda install -c "nvidia/label/cuda-11.7.1" cuda-toolkit
conda install pytorch==1.13.0 torchvision==0.14.0 torchaudio==0.13.0 pytorch-cuda=11.7 -c pytorch -c nvidia
pip install -r requirements.txt 

tiny-cuda-nn可以不装，主要用来加速。以下是安装步骤，我装了

conda install -c "nvidia/label/cuda-11.7.1" cuda-toolkit
pip install git+https://github.com/NVlabs/tiny-cuda-nn/#subdirectory=bindings/torch

2.如何使用

确保下载并解压相关数据在 data 文件夹中。以下有5个功能，可以选择使用

1. Image

• Data - Image Set

训练脚本在 scripts/2D_regression.ipynb,配置文件configs/image.yaml.

2. SDF

• Data - Mesh set

训练脚本在 scripts/sdf_regression.ipynb, 配置文件 configs/sdf.yaml.

3. NeRF

• Data - Synthetic-NeRF
• Data-Tanks&Temples

提供了以上两个数据集，训练脚本在 train_per_scene.py:

python train_per_scene.py configs/nerf.yaml defaults.expname=lego dataset.datadir=./data/nerf_synthetic/lego

4. 生成 Image

• Data - FFHQ

训练脚本在 2D_set_regression.ipynb

5. 稀疏重建 NeRF

• Data - Google Scanned Objects

python train_across_scene.py configs/nerf_set.yaml

以上是训练代码。训练完毕后，测试也是同一个py文件，后面可跟不同的参数：

• model.basis_dims=[4, 4, 4, 2, 2, 2] 调整levels ，channels 的数量, 总共 6 levels and 18 channels.
• model.basis_resos=[32, 51, 70, 89, 108, 128] 代表 feature embeddings 的分辨率
• model.freq_bands=[2.0, 3.2, 4.4, 5.6, 6.8, 8.0] indicates the frequency parameters applied at each level of the coordinate transformation function.
• model.coeff_type represents the coefficient field representations and can be one of the following: [none, x, grid, mlp, vec, cp, vm].
• model.basis_type represents the basis field representation and can be one of the following: [none, x, grid, mlp, vec, cp, vm, hash].
• model.basis_mapping represents the coordinate transformation and can be one of the following: [x, triangle, sawtooth, trigonometric]. Please note that if you want to use orthogonal projection, choose the cp or vm basis type, as they automatically utilize the orthogonal projection functions.
• model.total_params controls the total model size. It is important to note that the model’s size capability is determined by model.basis_resos and model.basis_dims. The total_params parameter mainly affects the capability of the coefficients.
• exportation.render_only you can rendering item after training by setting this label to 1. Please also specify the defaults.ckpt label.
• exportation.... you can specify whether to render the items of [render_test, render_train, render_path, export_mesh] after training by enable the corressponding label to 1.

Some pre-defined configurations (such as occNet, DVGO, nerf, iNGP, EG3D) can be found in README_FactorField.py.

3.代码解析

主要解析 few shot重建nerf的代码。网络主要由场景相关的 100个系数， 6 层的基，线性投影层和渲染层4部分组成。结构如下：

训练流程：

scene_idx = torch.randint(0, len(train_dataset.all_rgb_files), (1,)).item()      # 0-100个类中，随机选一个类
model.scene_idx = scene_idx
for j in range(steps_inner):                       # 循环 16 次
    if j%steps_inner==0:                           # 第一次循环，只放开coef的梯度
        model.set_optimizable(['coef'], True)
        model.set_optimizable(['proj','basis','renderer'], False)
    elif j%steps_inner==steps_inner-3:             # 第 13 次循环关闭 coef的梯度
        model.set_optimizable(['coef'], False)
        model.set_optimizable(['mlp', 'basis','renderer'], True)



    # 准备训练数据
    data = train_dataset[scene_idx] #next(iterator)                                       # 一个类有250张img
    rays_train, rgb_train = data['rays'].view(-1,6), data['rgbs'].view(-1,3).to(device)      # (4095,6) rgb:normed(4095,3) 


    # 开始渲染
    rgb_map, depth_map, coefffs = render_ray(rays_train, model, chunk=batch_size(4096),
                                    N_samples=449, white_bg=True, ndc_ray=0, device=device, is_train=True)
    
    # 计算损失
    loss = torch.mean((rgb_map - rgb_train) ** 2) #+ torch.mean(coefffs.abs())*1e-4
    PSNRs.append(-10.0 * np.log(loss) / np.log(10.0))

具体渲染函数 models/FactorFields.py FactorFields类的forward函数：

# 1.射线上采样------------------------------------------------------------------------------------
xyz_sampled, z_vals, inner_mask = self.sample_point(rays_chunk[:, :3], viewdirs, is_train=True,N_samples=443)

    # 具体展开
    def sample_point(self, rays_o, rays_d, is_train=True, N_samples=-1):
        N_samples = N_samples if N_samples > 0 else self.nSamples                 # 443
        vec = torch.where(rays_d == 0, torch.full_like(rays_d, 1e-6), rays_d)     # 把ray_d中为0的向量，设置为1e-6
        rate_a = (self.aabb[1, :self.in_dim] - rays_o) / vec                      # (4095,3) aabb[-1,-1,-1,1,1,1]中的起点和终点
        rate_b = (self.aabb[0, :self.in_dim] - rays_o) / vec
        # （射线的起点-最小边界）/射线方向，  得到射线与最小边界的交点位置
    

        t_min = torch.minimum(rate_a, rate_b).amax(-1).clamp(min=0.05, max=1e3)   # (4095) :0.05~0.33
        rng = torch.arange(N_samples)[None].float()                               # [1,2,3,...442]
        if is_train:
            rng = rng.repeat(rays_d.shape[-2], 1)
            rng += torch.rand_like(rng[:, [0]])                                   # (4095,443) + noise
        step = self.stepSize * rng.to(rays_o.device)                              # self.stepSize = 0.0079 (4095,443):0.0032~3.2
        interpx = (t_min[..., None] + step)

        rays_pts = rays_o[..., None, :] + rays_d[..., None, :] * interpx[..., None]    # (4095,443,3) -2.4~2.6
        mask_outbbox = ((self.aabb[0, :self.in_dim] > rays_pts) | (rays_pts > self.aabb[1, :self.in_dim])).any(dim=-1)    #  # (4095,443):mask

        return rays_pts, interpx, ~mask_outbbox

dists = torch.cat((z_vals[:, 1:] - z_vals[:, :-1], torch.zeros_like(z_vals[:, :1])), dim=-1)

viewdirs = viewdirs.view(-1, 1, 3).expand(xyz_sampled.shape)      # (4095,443,3)
ray_valid = torch.ones_like(xyz_sampled[..., 0]).bool() if self.is_unbound else inner_mask    # mask:立方体内的点

# 2.采样点 坐标变换：------------------------------------------------------------------------------------
 
    # 001 在标准立方体内，对三维点做归一化
    pts = self.normalize_coord(xyz_sampled).view([1, -1] + [1] * (dim - 1) + [dim])
          def normalize_coord(self, xyz_sampled):
              invaabbSize = 2.0 / (self.aabb[1] - self.aabb[0])      # [1,1,1]
              return (xyz_sampled - self.aabb[0]) * invaabbSize - 1

    # 002 这步主要计算coeff 和 basises，详细过程在下面
    feats, coeffs = self.get_coding(xyz_sampled[ray_valid])
        
            coeff = self.get_coeff(x)             # x：(1103929,3) 有效点的坐标
                    if 'grid' in self.coeff_type:
                       # 非hash采样： self.coeffs[self.scene_idx]初始化为(1,72,16,16,16)*[1]， 在特征体内，采样点的特征系数 得到结果：(1103929,72)
                        coeffs = F.grid_sample(self.coeffs[self.scene_idx], pts, mode=self.cfg.model.coef_mode, align_corners=False,
                                  padding_mode='border').view(-1, N_points).t()      

            basises = []
            for i in range(freq_len):
                basises = self.get_basis(x)
                    xyz = grid_mapping(x, self.freq_bands , self.aabb[:, :self.in_dim], self.cfg.model.basis_mapping).view(1, *( [1] * (3 - 1)), -1, 3, freq_len=6)
                          def grid_mapping(positions, freq_bands, aabb, basis_mapping='sawtooth'):
                              aabbSize = max(aabb[1] - aabb[0])       # 2
                              scale = aabbSize[..., None] / freq_bands   # freq_bands: [2.0, 3.2, 4.4, 5.6, 6.8, 8]  -> [1.0, 0.62, 0.45,..., 0.25]
                              if basis_mapping == 'sawtooth':
                                 pts_local = (positions - aabb[0])[..., None] % scale    # (1103929,3,6)
                                 pts_local = pts_local / (scale / 2) - 1
                                 pts_local = pts_local.clamp(-1., 1.)
               basises = torch.cat(basises, dim=-1)    # (6, 1103929, 16) --> (1103929, 72) 

            basises * coeff, coeff

    # 003 MLP 得到密度和颜色
    feat = self.linear_mat(feats, is_train=is_train)           # (1103929, 72) -MLP-> (1103929, 32)
    sigma[ray_valid] = self.basis2density(feat[..., 0])        # F.softplus -> (1103929)

    alpha, weight, bg_weight = raw2alpha(sigma, dists * self.cfg.renderer.distance_scale)   # dists*25   nerf中的积分公式。详情可见论文 alpha(4095,443) w(4095,443) b(4095)

    # 筛选背景，以及weight小于0.001的射线
    app_mask = weight > self.cfg.renderer.rayMarch_weight_thres                      # 0.001
    ray_valid_new = torch.logical_and(ray_valid, app_mask)
    app_mask = ray_valid_new[ray_valid] 

if app_mask.any():             
    # 训练后期才会出现 True 的情况
    valid_rgbs = self.renderModule(viewdirs[ray_valid_new], feat[app_mask, 1:])
                      # 以下代码，先用正余弦编码升到高维，再用 mlp 降维
                      indata += [positional_encoding(features, self.feape)]     # self.feape =2
                                 def positional_encoding(positions, freqs):
                                     freq_bands = (2 ** torch.arange(freqs).float()).to(positions.device)  # (F,) freqs=2  --> [1,2]
                                     pts = (positions[..., None] * freq_bands).reshape(positions.shape[:-1] + (freqs * positions.shape[-1],))  # (..., DF)  (131,31) -> (131,62)
                                     pts = torch.cat([torch.sin(pts), torch.cos(pts)], dim=-1)    # (131,62) -> (131,124)
                                     return pts

                      indata += [positional_encoding(viewdirs, self.viewpe)]    # self.viewpe

                      h = torch.cat(indata, dim=-1)          # (131,194)
                      for l in range(self.num_layers):       # 3 layer
                          h = self.mlp[l](h)
                          if l != self.num_layers - 1:
                             h = F.relu(h, inplace=True)
                      rgb = torch.sigmoid(h)

    rgb[ray_valid_new] = valid_rgbs


acc_map = torch.sum(weight, -1)
rgb_map = torch.sum(weight[..., None] * rgb, -2)

rgb_map = rgb_map + (1. - acc_map[..., None])  if white_bg

rgb_map = rgb_map.clamp(0, 1)

with torch.no_grad():
    depth_map = torch.sum(weight * z_vals, -1)

额外函数

init_basis初始化为：

self.basises = self.init_basis()
def init_basis(self) 如下

elif 'grid' in self.basis_type:
     basises.append(torch.nn.Parameter(dct_dict(int(np.power(basis_dim, 1. / self.in_dim) + 1), reso,     n_selete=basis_dim, dim=self.in_dim).reshape(
                    [1, basis_dim] + [reso] * self.in_dim).to(self.device)))



def dct_dict(n_atoms_fre, size, n_selete, dim=2):
    """
    Create a dictionary using the Discrete Cosine Transform (DCT) basis. If n_atoms is
    not a perfect square, the returned dictionary will have ceil(sqrt(n_atoms))**2 atoms
    :param n_atoms:
        Number of atoms in dict
    :param size:
        Size of first patch dim
    :return:
        DCT dictionary, shape (size*size, ceil(sqrt(n_atoms))**2)
    """
    # todo flip arguments to match random_dictionary
    p = n_atoms_fre  # int(math.ceil(math.sqrt(n_atoms)))
    dct = np.zeros((p, size))

    for k in range(p):
        basis = np.cos(np.arange(size) * k * math.pi / p)
        if k > 0:
            basis = basis - np.mean(basis)

        dct[k] = basis

    kron = np.kron(dct, dct)
    if 3 == dim:
        kron = np.kron(kron, dct)

    if n_selete < kron.shape[0]:
        idx = [x[0] for x in np.array_split(np.arange(kron.shape[0]), n_selete)]
        kron = kron[idx]

    for col in range(kron.shape[0]):
        norm = np.linalg.norm(kron[col]) or 1
        kron[col] /= norm

    kron = torch.FloatTensor(kron)
    return kron

获取射线的原点和方向（输入是一张图像，及其对应的内参、外参）

def get_ray_directions(H, W, focal, center=None):
    """
    得到射线的方向
    Inputs:
        H, W, focal: image height, width and focal length
    Outputs:
        directions: (H, W, 3), the direction of the rays in camera coordinate
    """
    grid = create_meshgrid(H, W, normalized_coordinates=False)[0] + 0.5

    i, j = grid.unbind(-1)
    # the direction here is without +0.5 pixel centering as calibration is not so accurate
    # see https://github.com/bmild/nerf/issues/24
    cent = center if center is not None else [W / 2, H / 2]
    directions = torch.stack([(i - cent[0]) / focal[0], (j - cent[1]) / focal[1], torch.ones_like(i)], -1)  # (H, W, 3)

    return directions


def get_rays(directions, c2w):
    """
   得到射线的起点和方向
    Inputs:
        directions: (H, W, 3) precomputed ray directions in camera coordinate
        c2w: (3, 4) transformation matrix from camera coordinate to world coordinate
    Outputs:
        rays_o: (H*W, 3), the origin of the rays in world coordinate
        rays_d: (H*W, 3), the normalized direction of the rays in world coordinate
    """
    # Rotate ray directions from camera coordinate to the world coordinate
    rays_d = directions @ c2w[:3, :3].T  # (H, W, 3) (512,512,3)
    # rays_d = rays_d / torch.norm(rays_d, dim=-1, keepdim=True)
    # The origin of all rays is the camera origin in world coordinate
    rays_o = c2w[:3, 3].expand(rays_d.shape)  # (H, W, 3)

    rays_d = rays_d.view(-1, 3)
    rays_o = rays_o.view(-1, 3)

    return rays_o, rays_d