什么是数组
数组:可以看成是相同类型元素的一个集合。在内存中是一段连续的空间。
在java中,
- 数组中存放的元素其类型相同
- 数组的空间是连在一起的
- 每个空间有自己的编号,起始位置的编号为0,即数组的下标。
数组的创建及初始化

数组的初始化
动态初始化:在创建数组时,直接指定数组中元素的个数(可以看到这里面全部存储的0)

静态初始化:在创建数组时不直接指定数据元素个数,而直接将具体的数据内容进行指定

静态初始化可以简写,省去后面的new T[]。
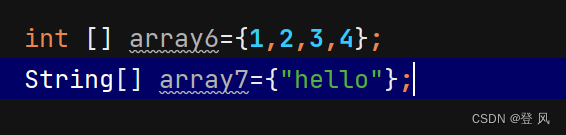
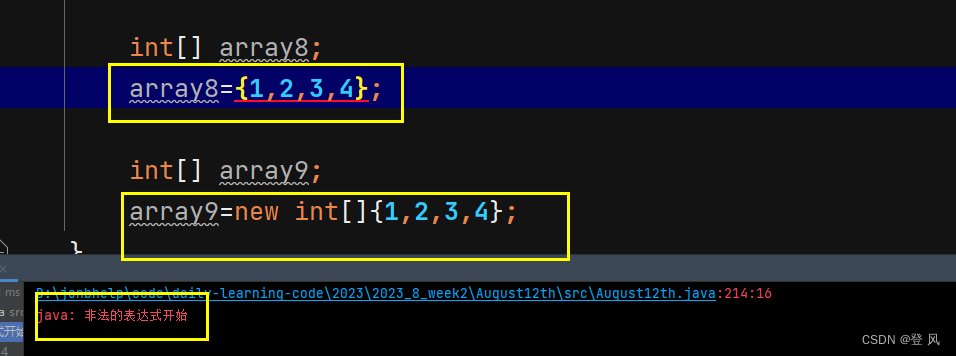
静态和动态初始化也可以分为两步,但是省略格式不可以。
如果数组中存储元素类型为基类类型,默认值为基类类型对应的默认值
boolean类的默认值为false
如果数组中存储元素类型为引用类型,默认值为null,如:
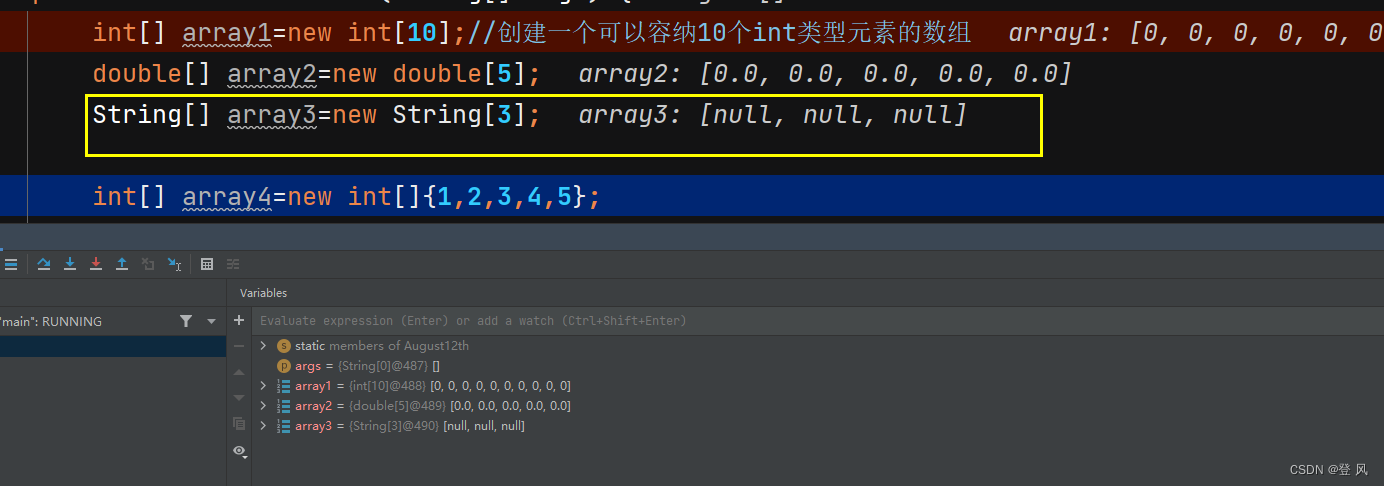
数组中元素访问
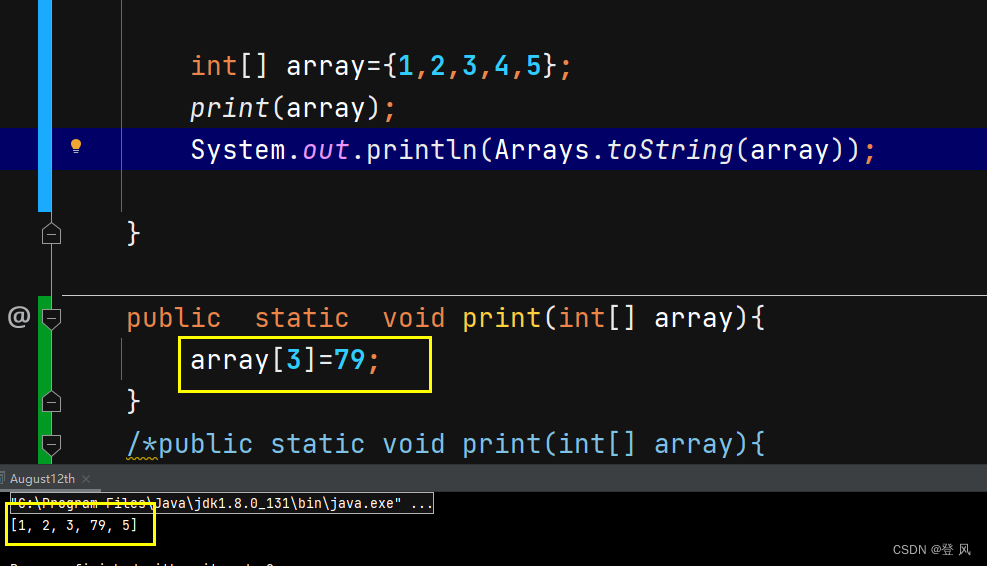
数组可以通过
下标访问其任意位置的元素,也可以通过[]对数组中的元素进行修改
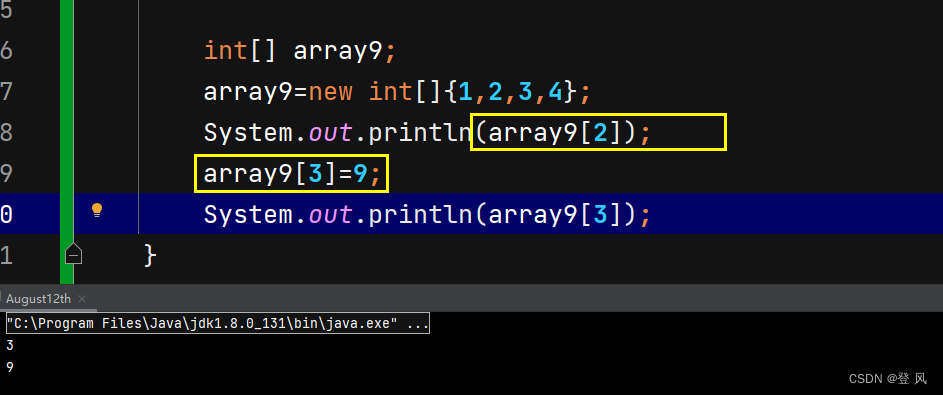
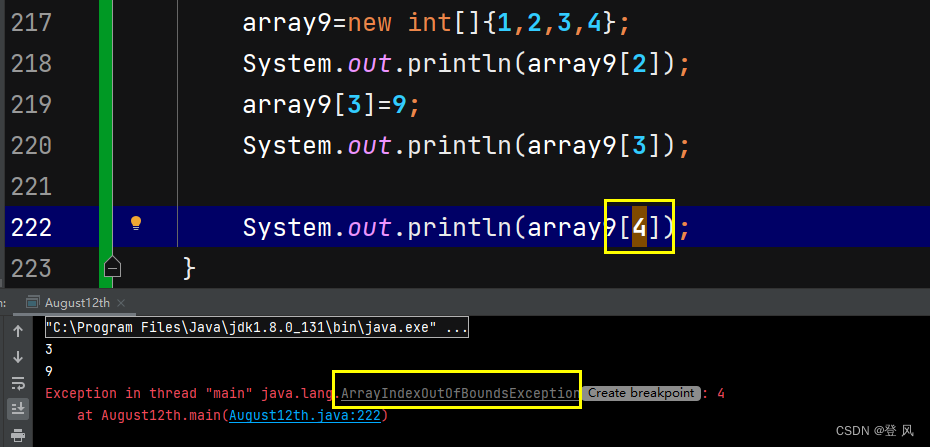
下标从0开始,介于[0, N)之间不包含N,N为元素个数,不能越界,否则会报出下标越界异常。
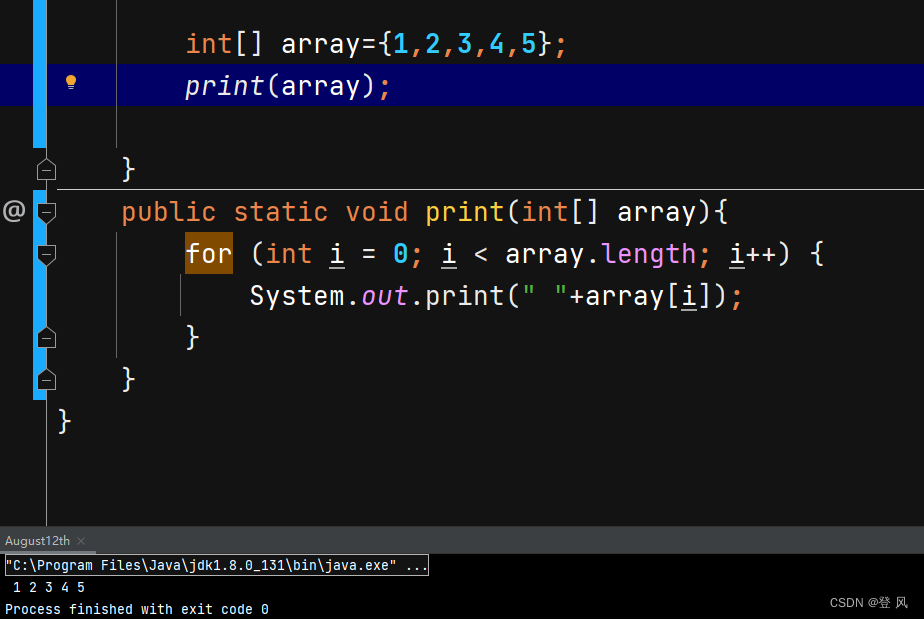
遍历数组
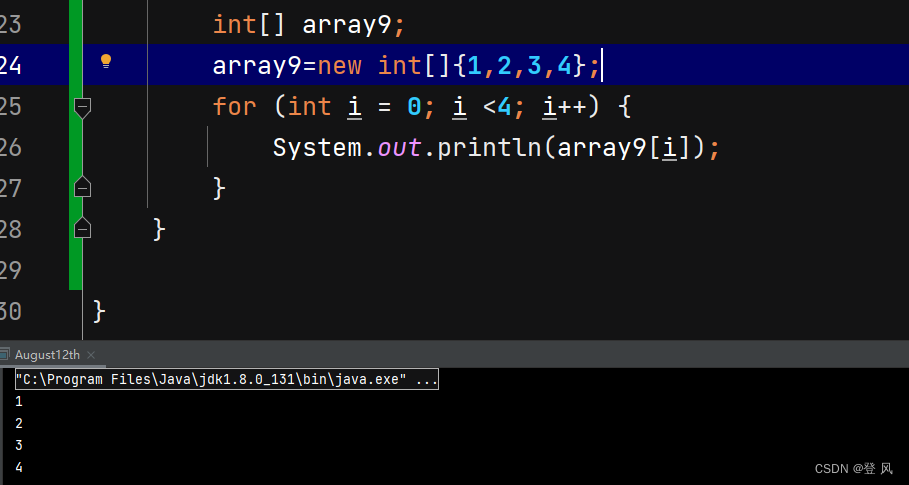
在数组中可以通过 数组对象.length 来获取数组的长度
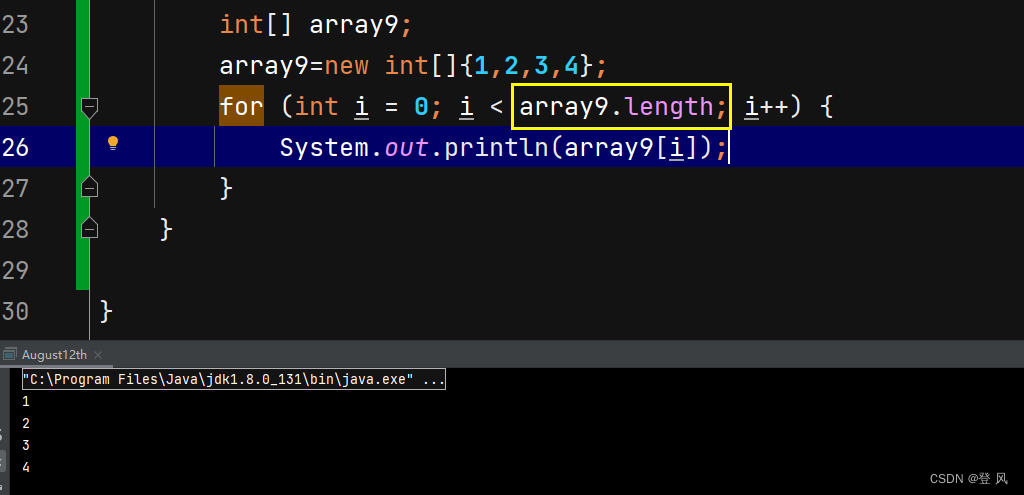
也可以使用 for-each 遍历数组
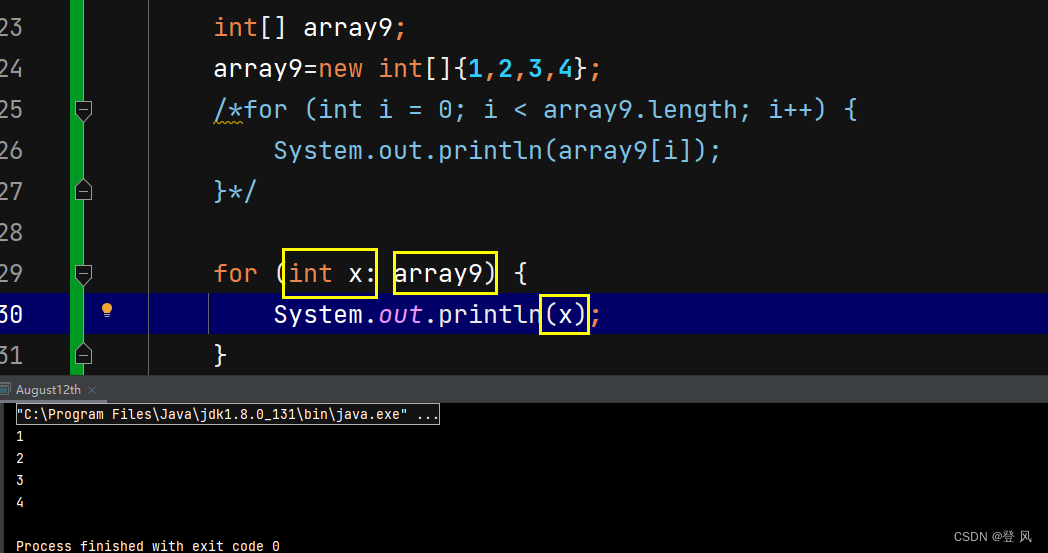



数组是引用类型
JVM也对所使用的内存按照功能的不同进行了划分
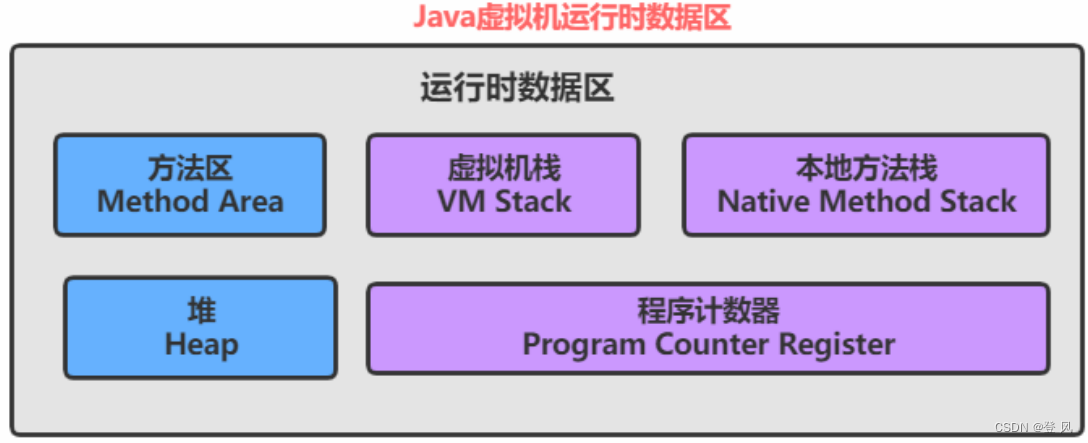
现在我们只简单关心堆 和 虚拟机栈这两块空间
堆(Heap): JVM所管理的最大内存区域. 使用 new 创建的对象都是在堆上保存 (例如前面的 new int[]{1, 2,3} ),堆是随着程序开始运行时而创建,随着程序的退出而销毁,堆中的数据只要还有在使用,就不会被销毁。
虚拟机栈(JVM Stack): 与方法调用相关的一些信息,每个方法在执行时,都会先创建一个栈帧,栈帧中包含有:局部变量表、操作数栈、动态链接、返回地址以及其他的一些信息,保存的都是与方法执行时相关的一些信息。比如:局部变量。当方法运行结束后,栈帧就被销毁了,即栈帧中保存的数据也被销毁了。

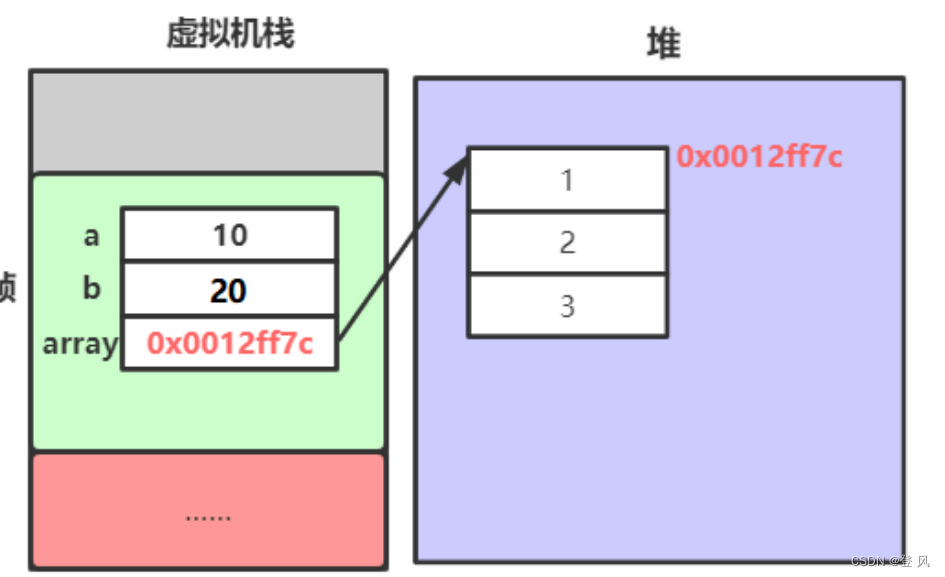

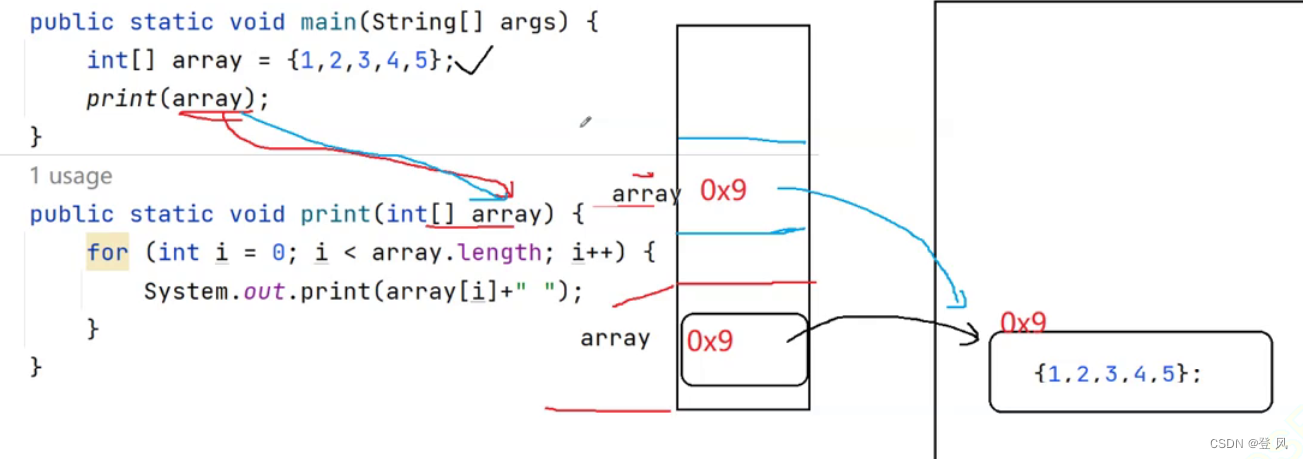
这个array变量里面存放的是一个地址。
引用数据类型创建的变量,一般称为对象的引用,其空间中存储的是对象所在空间的地址。
null 在 Java 中表示 “空引用” , 也就是一个不指向对象的引用.
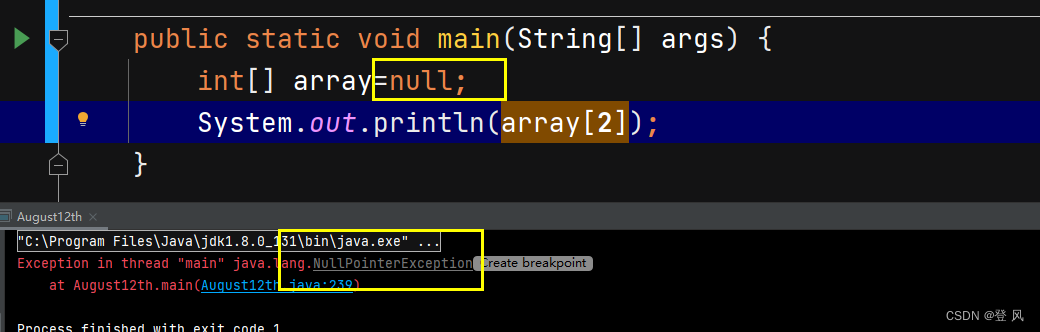

与上图的对比
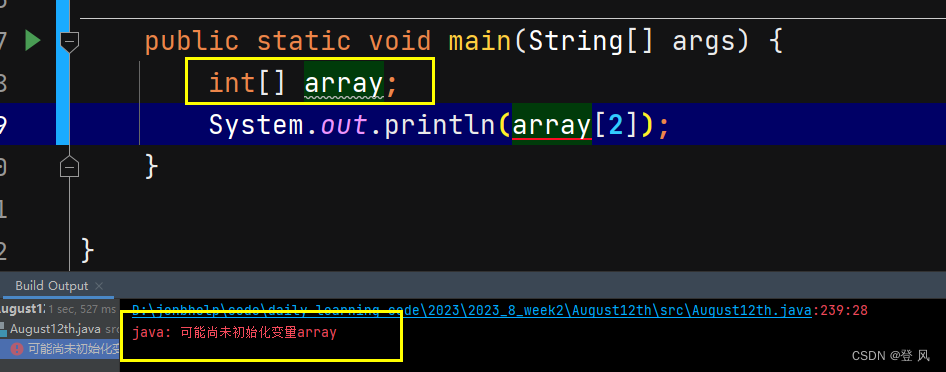
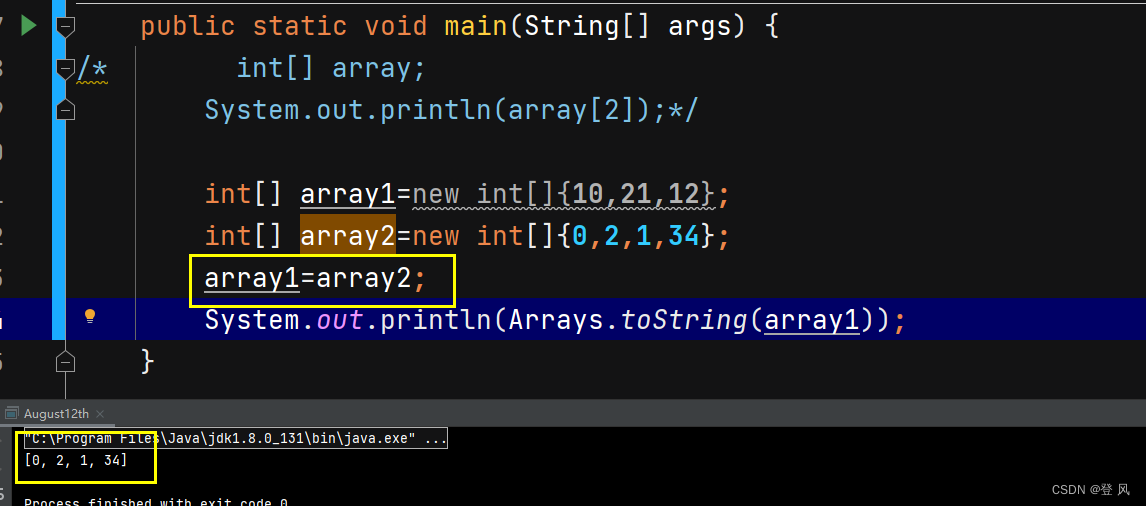
array1这个引用指向的对象会自动回收掉
作为函数的参数
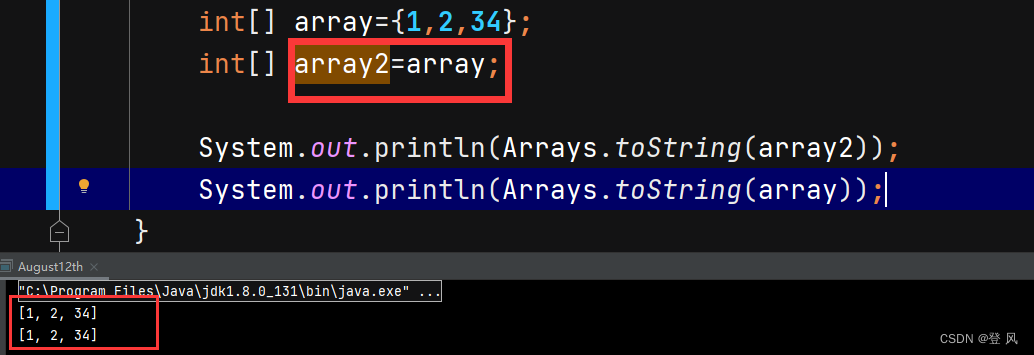
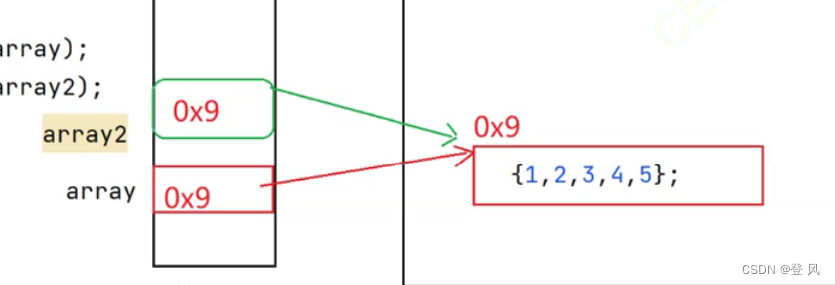
array2这个引用指向了array这个引用所指向的对象
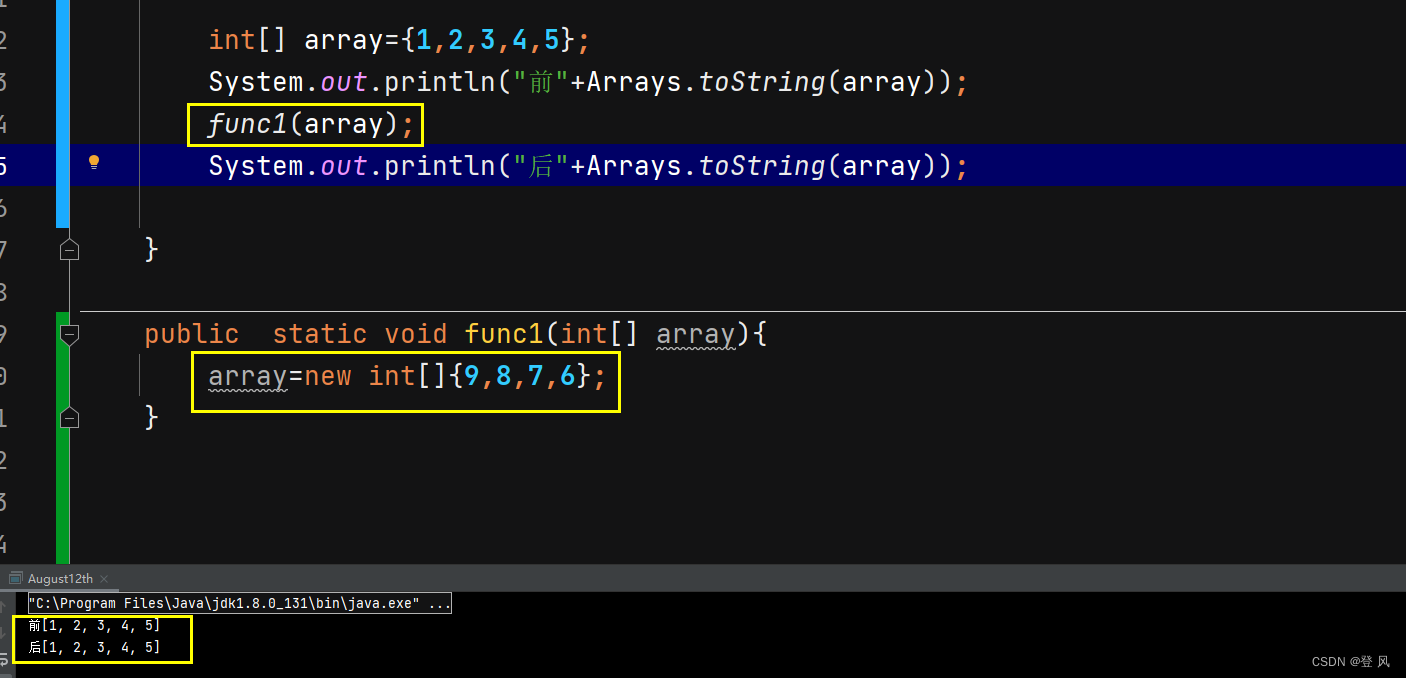
这里new int[]{9,8,7,6};让形参指向了一个新的对象,形参array内存放的地址发生了变化。即使对形参array操作,也不会改变实参

不一定,如上
作为函数的返回值

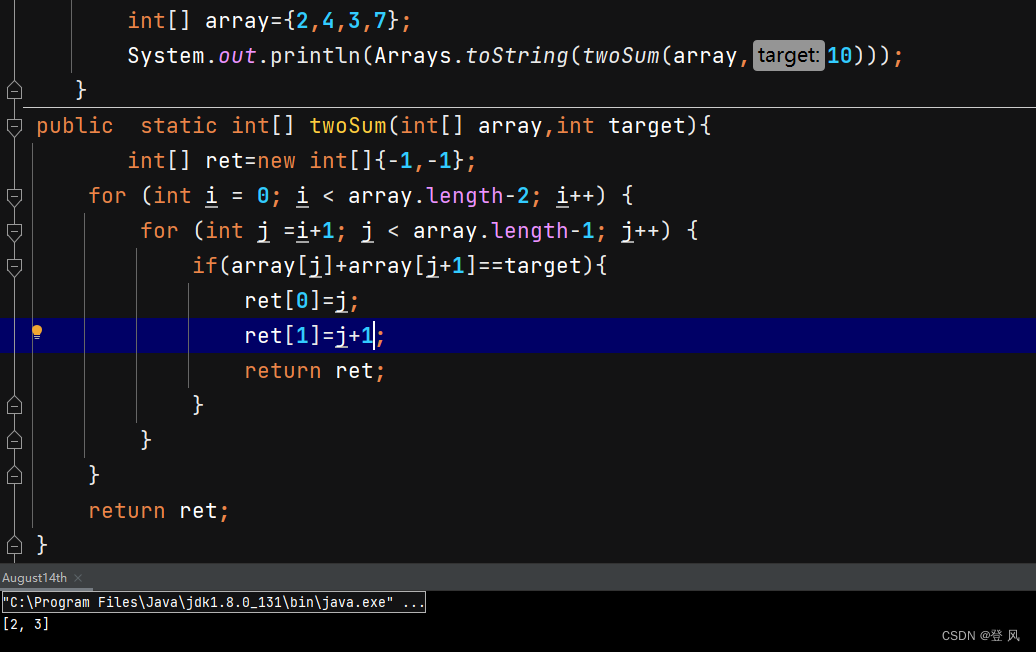
可以传回多个返回值
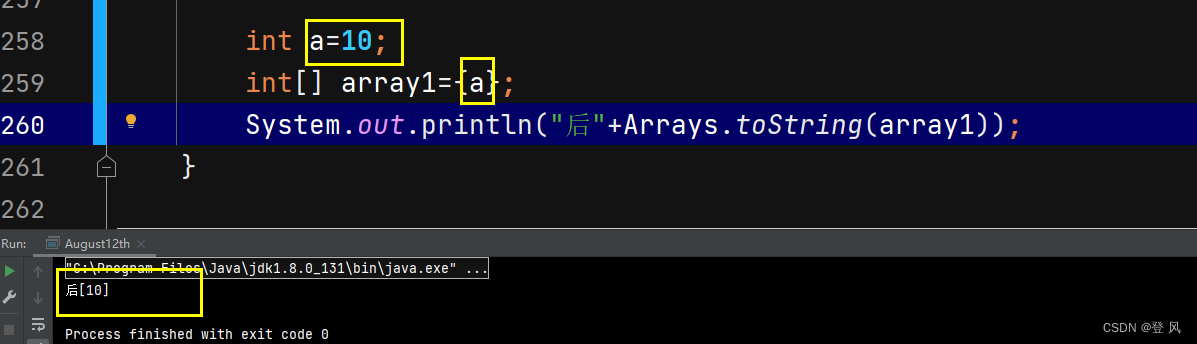
数组的元素可以为变量。
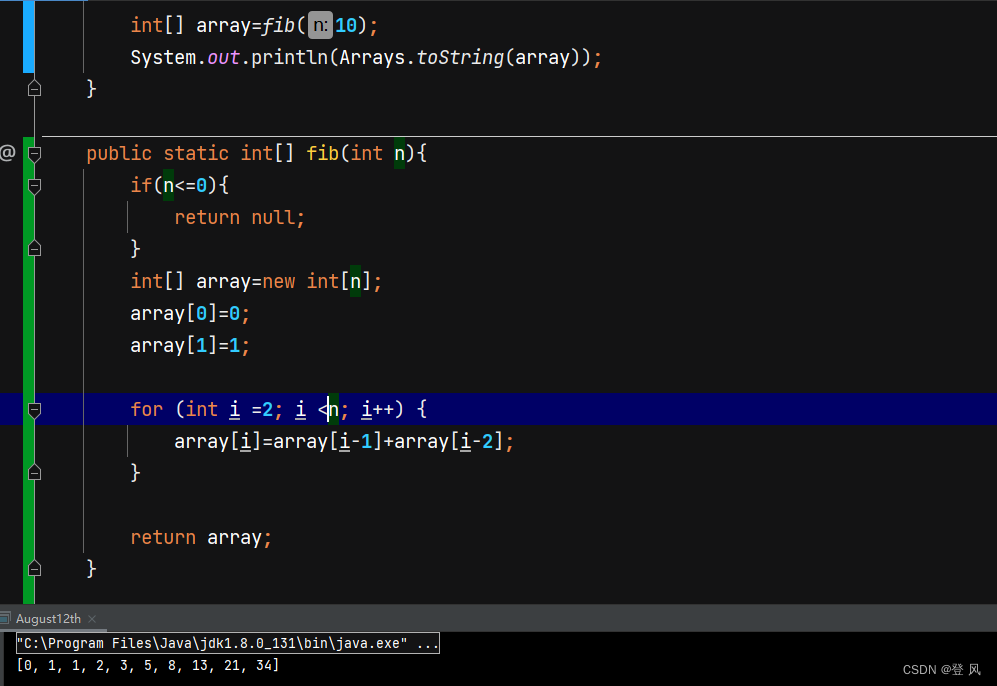
获取斐波那契数列的前N项
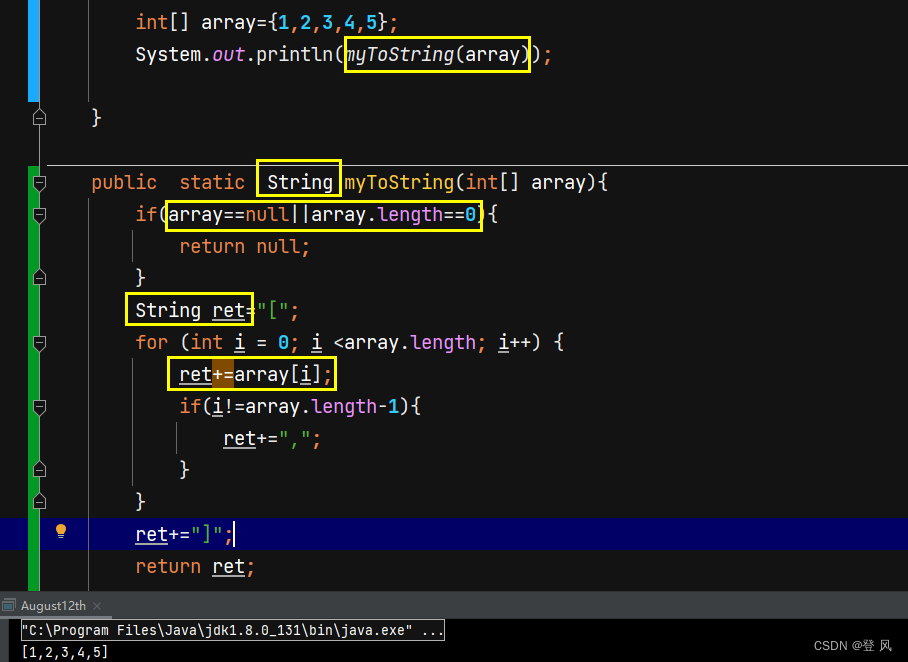
模拟实现Arrays.toString(array)
实现数组拷贝
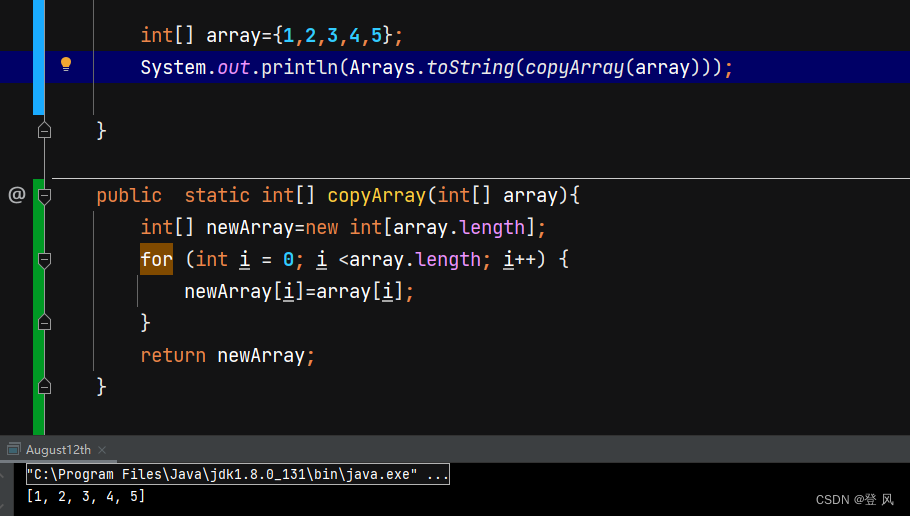
新建立一块空间
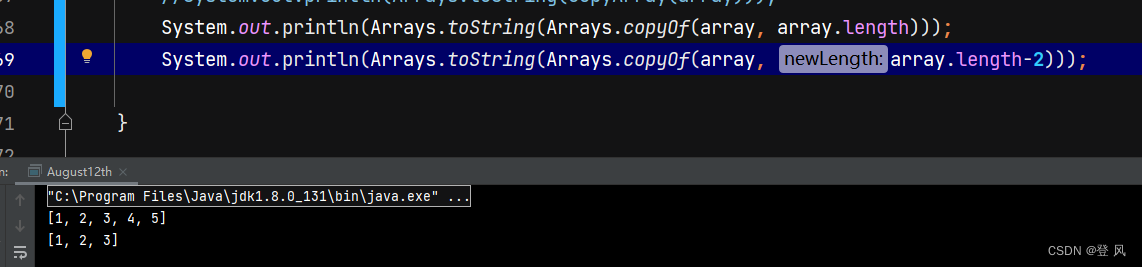
使用Arrays.copyOf,第一个参数为数组名,第二个参数为需要拷贝的长度。函数返回值为一个数组
该函数还可以扩充数组的容量

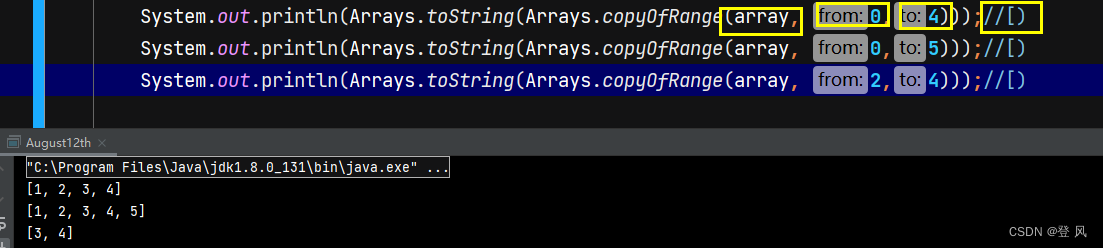
使用Arrays.copyOfRange,第一个参数为数组名,第二个参数为拷贝的起始下标,第三个参数为拷贝的最后下标,注意拷贝区间的左闭右开。

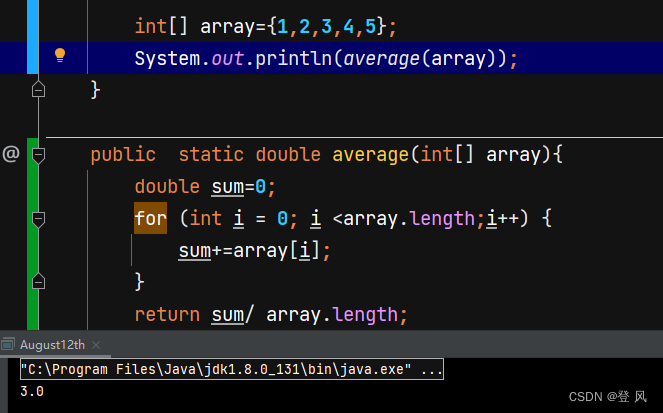
求数组中元素的平均值
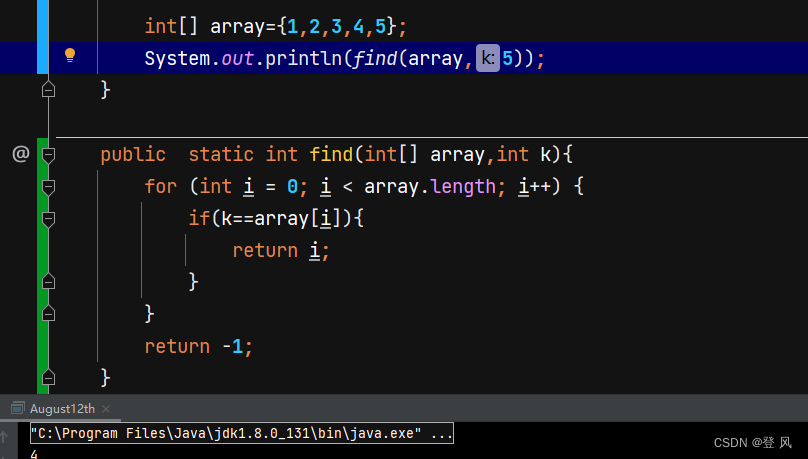
查找数组中指定元素(顺序查找)
查找数组中指定元素(二分查找)
针对有序数组, 可以使用更高效的二分查找.
以升序数组为例, 二分查找的思路是先取中间位置的元素, 然后使用待查找元素与数组中间元素进行比较:
如果相等,即找到了返回该元素在数组中的下标
如果小于,以类似方式到数组左半侧查找
如果大于,以类似方式到数组右半侧查找
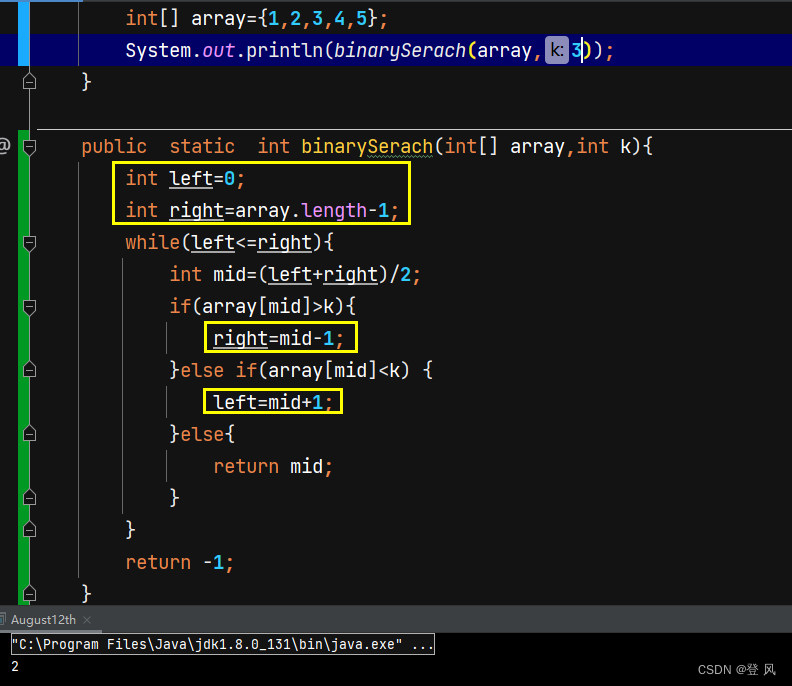
java自带的二分查找
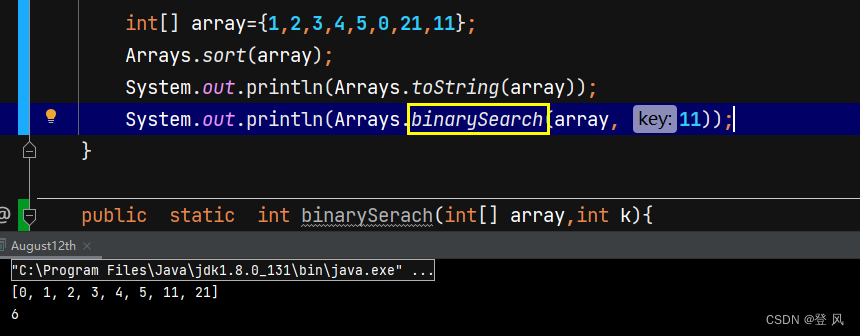
Arrays.binarySearch,第一个参数是数组名,第二个参数是要查找的数值
将无序数组变为有序数组
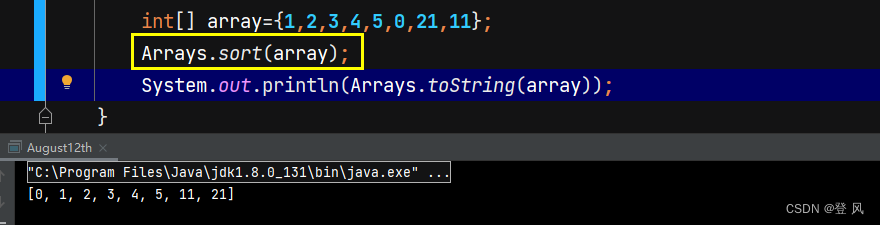
使用Arrays.sort
数组排序(冒泡排序)
假设排升序:
- 将数组中相邻元素从前往后依次进行比较,如果前一个元素比后一个元素大,则交换,一趟下来后最大元素就在数组的末尾
- 依次从上上述过程,直到数组中所有的元素都排列好
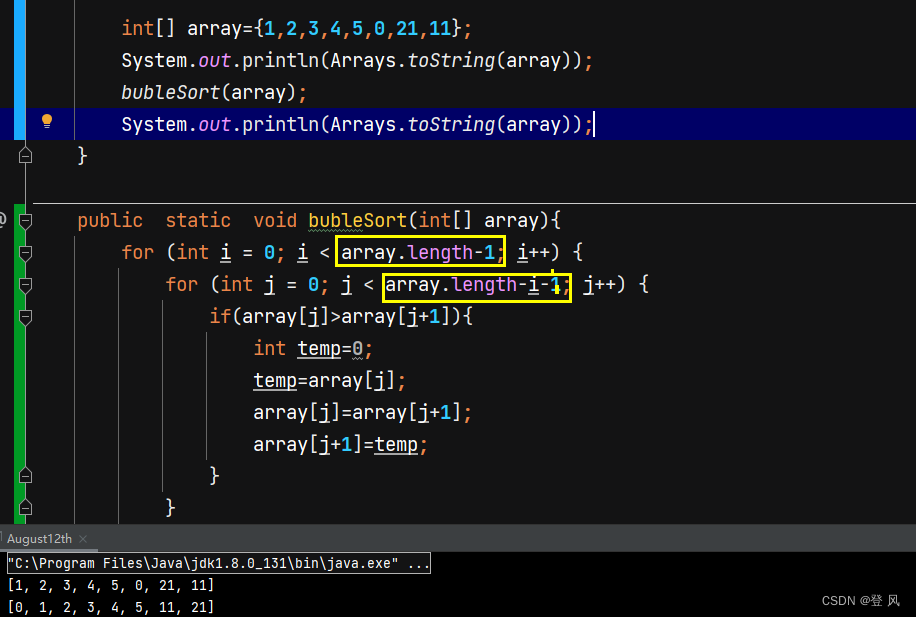
优化上述代码
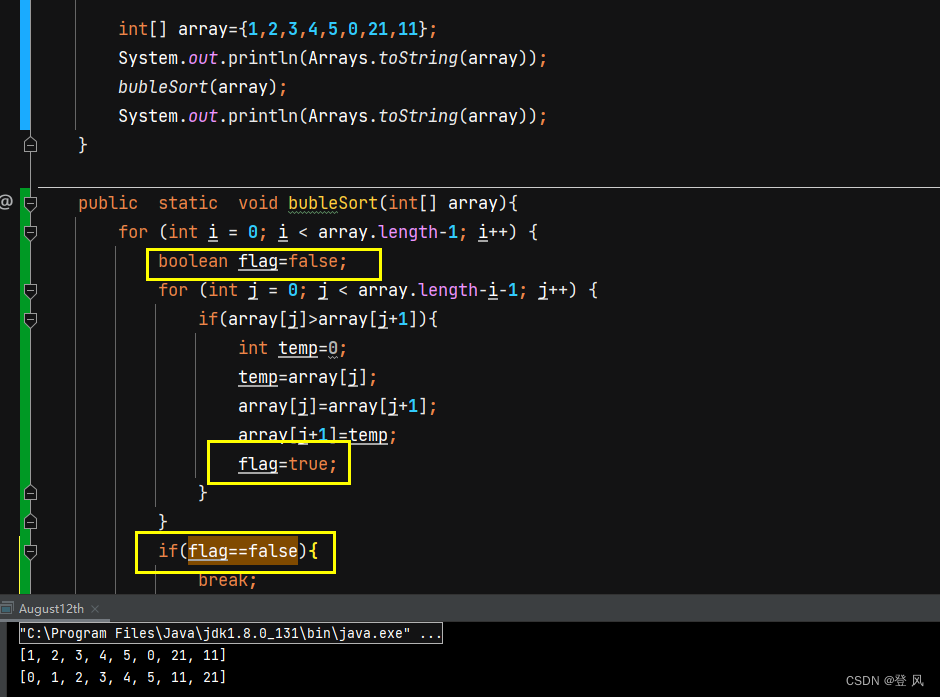
在1次冒泡中如果没有交换位置,那表明已经是有序的了,可以直接跳出循环。
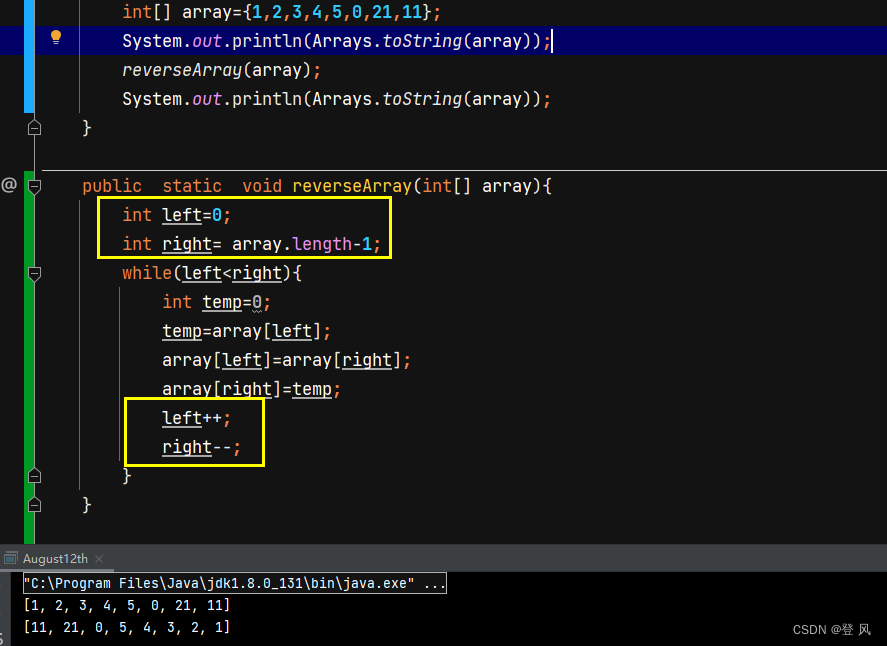
数组逆序
给定一个数组, 将里面的元素逆序排列.
思路
设定两个下标, 分别指向第一个元素和最后一个元素. 交换两个位置的元素;然后让前一个下标自增, 后一个下标自减, 循环继续即可.
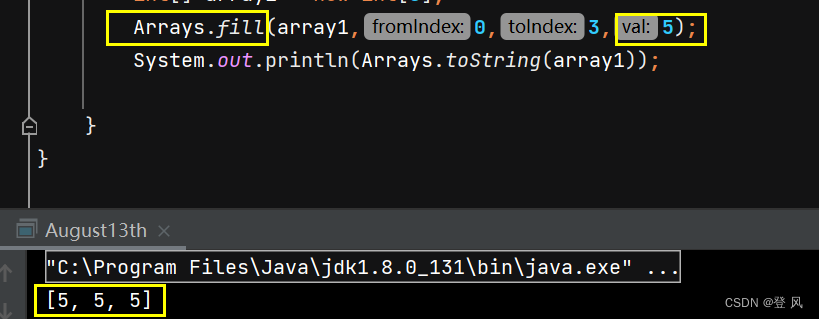
二维数组

二维数组的遍历
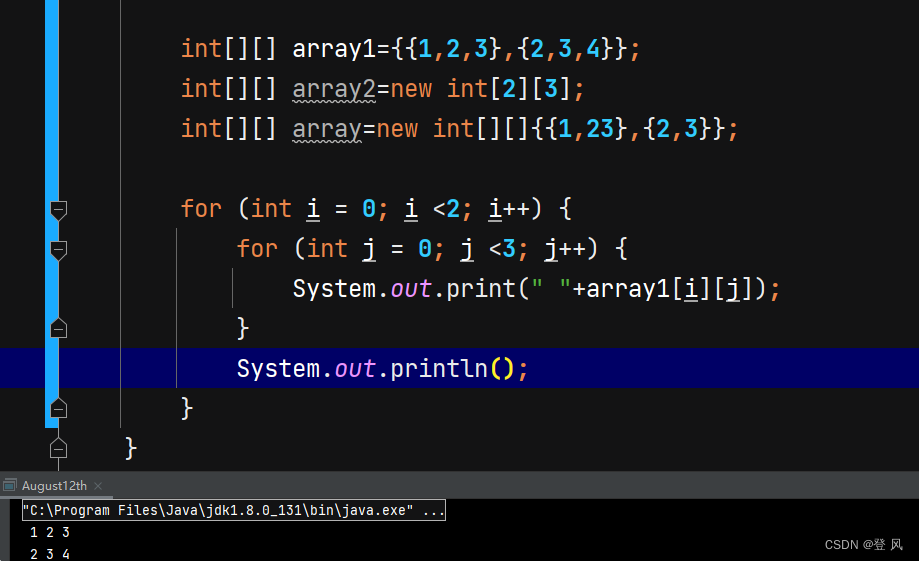
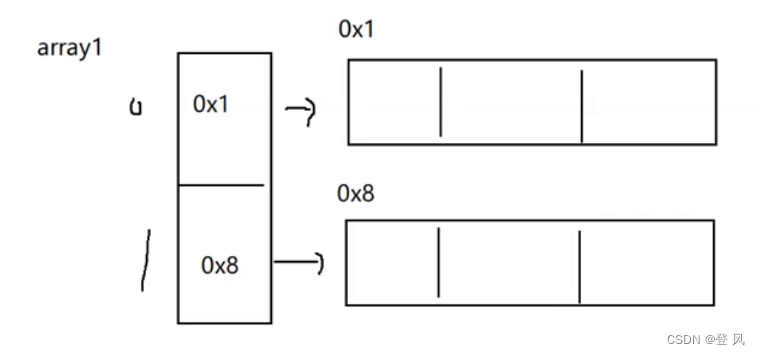
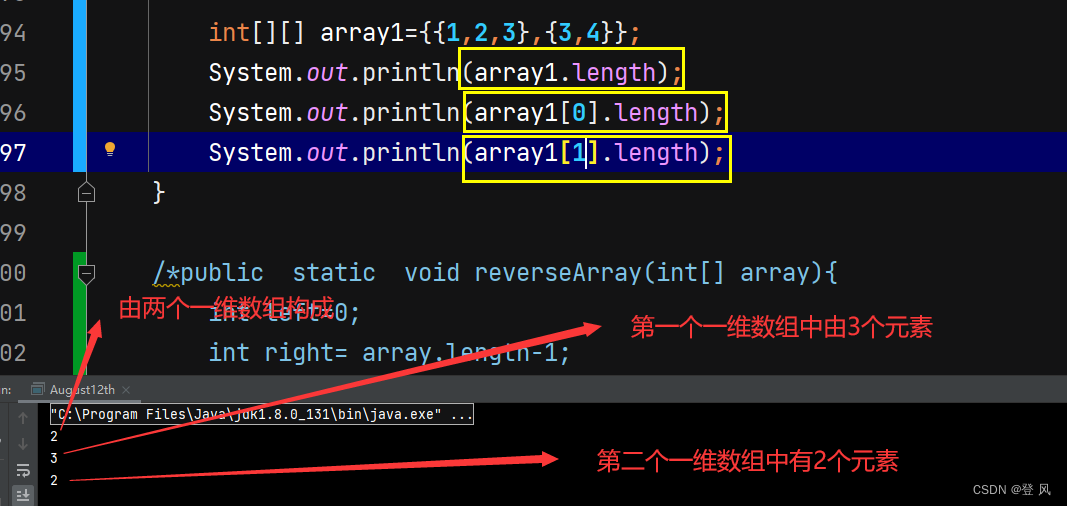
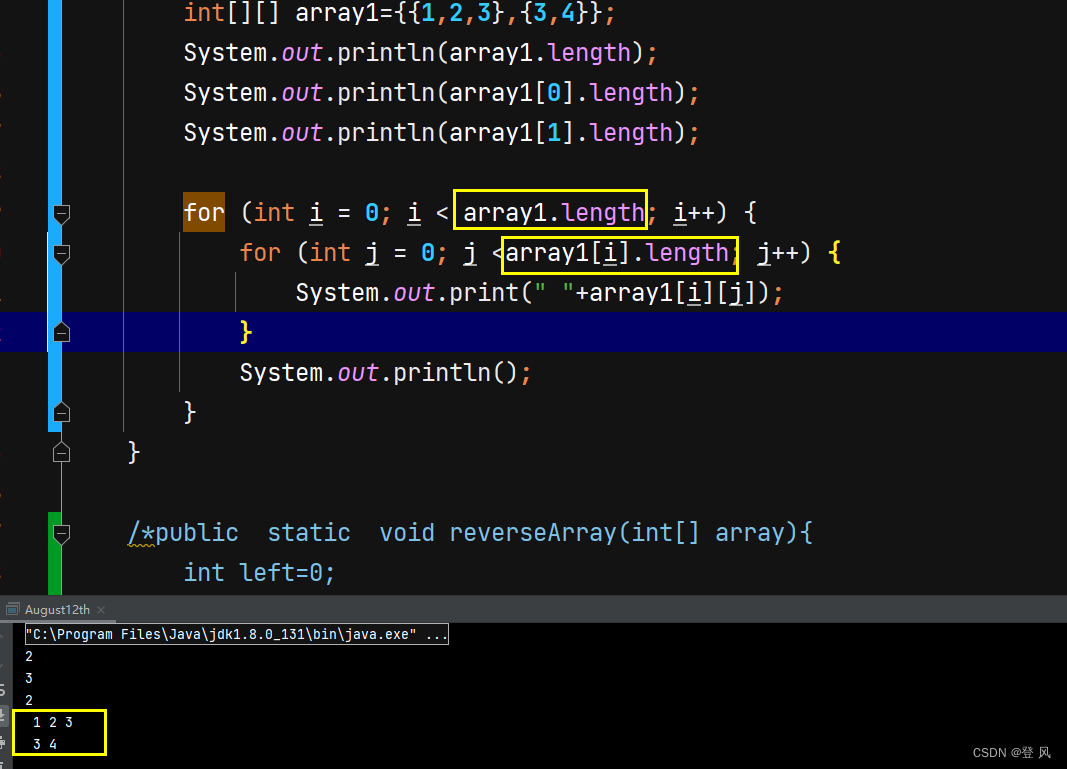
于是,一种新的遍历方式
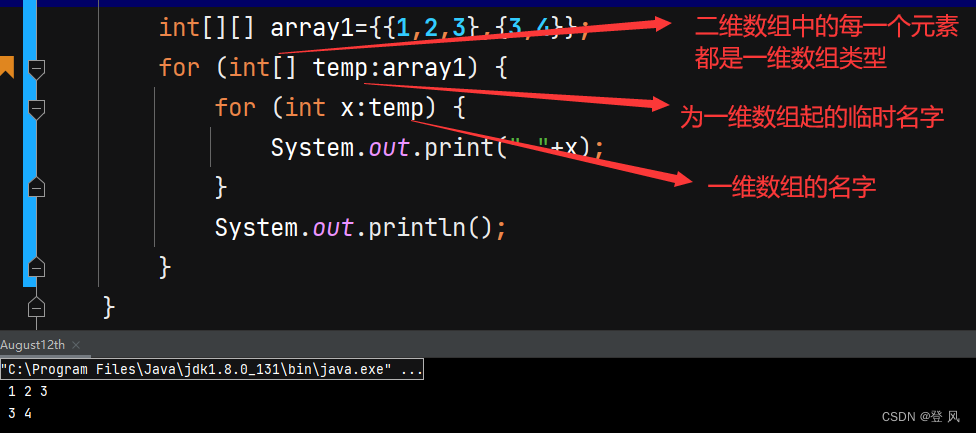
利用foreach来遍历
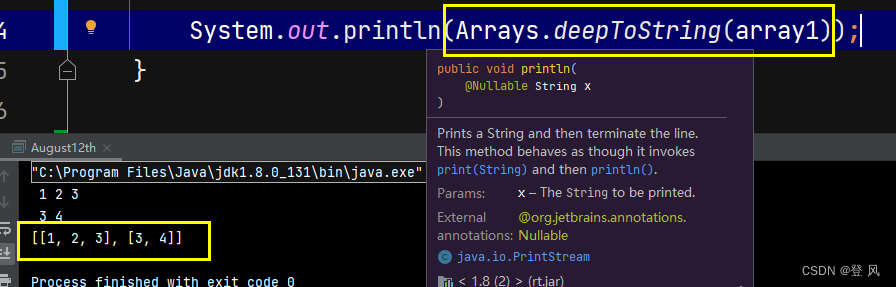
利用Arrays.deepToString直接打印
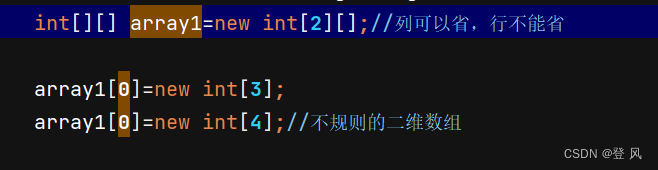
创建一个 int 类型的数组, 元素个数为 100, 并把每个元素依次设置为 1 - 100
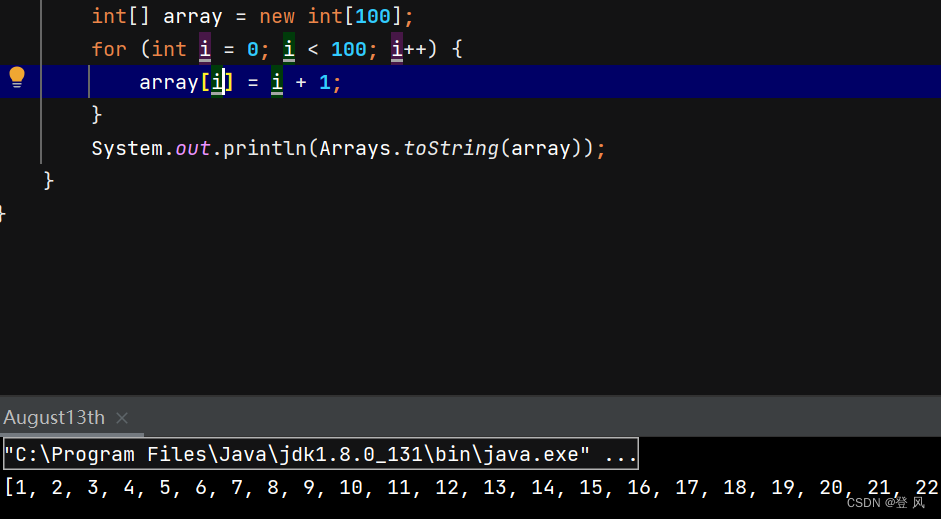
Arrays.fill 将指定的字节值分配给指定字节数组的指定范围的每个元素
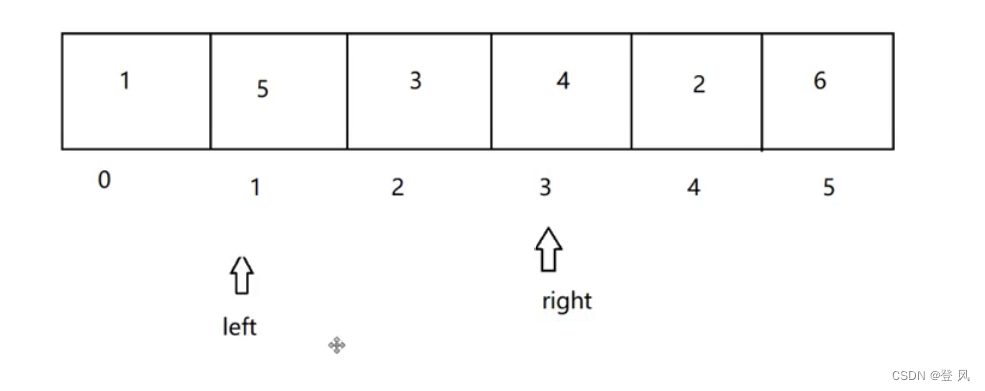
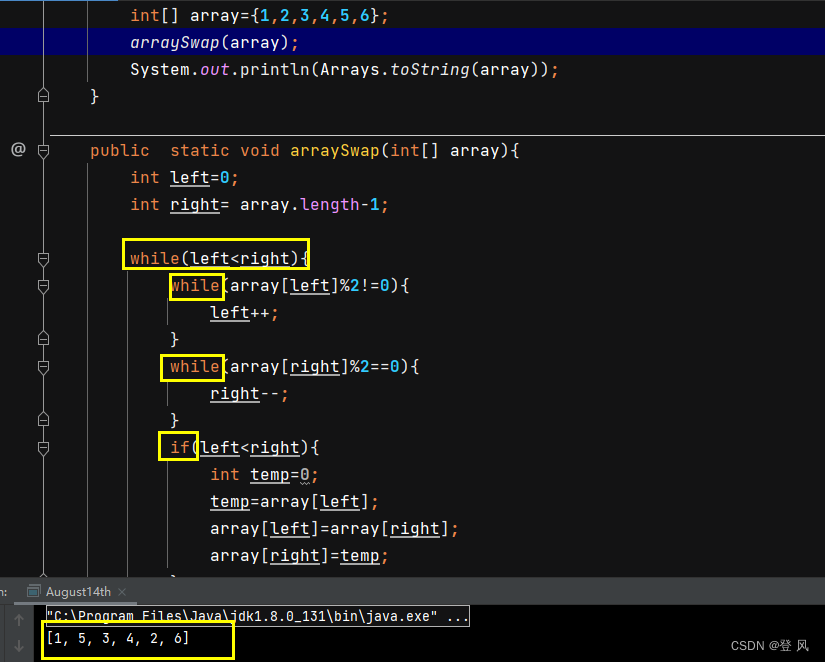
调整数组顺序使得奇数位于偶数之前。调整之后,不关心大小顺序。
如数组:[1,2,3,4,5,6]
调整后可能是:[1, 5, 3, 4, 2, 6]
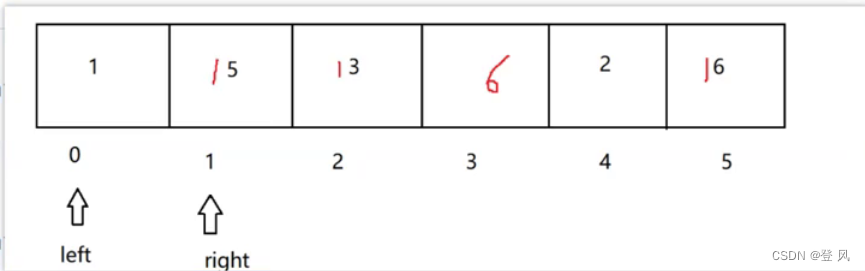
使用两个指针left和right,一个从左,一个从右;
左边遇到偶数,记录下来,准备和右边的进行交换
右边遇到奇数,记录下来,准备和左边交换