LRU 缓存淘汰算法就是一种常用策略。LRU 的全称是 Least Recently Used,也就是说我们认为最近使用过的数据应该是是「有用的」,很久都没用过的数据应该是无用的,内存满了就优先删那些很久没用过的数据。
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 LRU算法题
一、LRU 算法描述
首先要接收一个 capacity 参数作为缓存的最大容量,然后实现两个 API,一个是 put(key, val) 方法存入键值对,另一个是 get(key) 方法获取 key 对应的 val,如果 key 不存在则返回 -1。
注意:get 和 put 方法必须都是 O(1) 的时间复杂度,我们举个具体例子来看看 LRU 算法怎么工作
/* 缓存容量为 2 */ LRUCache cache = new LRUCache(2); // 你可以把 cache 理解成一个队列 // 假设左边是队头,右边是队尾 // 最近使用的排在队头,久未使用的排在队尾 // 圆括号表示键值对 (key, val) cache.put(1, 1); // cache = [(1, 1)] cache.put(2, 2); // cache = [(2, 2), (1, 1)] cache.get(1); // 返回 1 // cache = [(1, 1), (2, 2)] // 解释:因为最近访问了键 1,所以提前至队头 // 返回键 1 对应的值 1 cache.put(3, 3); // cache = [(3, 3), (1, 1)] // 解释:缓存容量已满,需要删除内容空出位置 // 优先删除久未使用的数据,也就是队尾的数据 // 然后把新的数据插入队头 cache.get(2); // 返回 -1 (未找到) // cache = [(3, 3), (1, 1)] // 解释:cache 中不存在键为 2 的数据 cache.put(1, 4); // cache = [(1, 4), (3, 3)] // 解释:键 1 已存在,把原始值 1 覆盖为 4 // 不要忘了也要将键值对提前到队头
二、LRU 算法设计
分析上面的操作过程,要让 put 和 get 方法的时间复杂度为 O(1),我们可以总结出 cache 这个数据结构必要的条件:
1、显然 cache 中的元素必须有时序,以区分最近使用的和久未使用的数据,当容量满了之后要删除最久未使用的那个元素腾位置。
2、我们要在 cache 中快速找某个 key 是否已存在并得到对应的 val;
3、每次访问 cache 中的某个 key,需要将这个元素变为最近使用的,也就是说 cache 要支持在任意位置快速插入和删除元素。
那么,什么数据结构同时符合上述条件呢?哈希表查找快,但是数据无固定顺序;链表有顺序之分,插入删除快,但是查找慢。所以结合一下,形成一种新的数据结构:哈希链表 LinkedHashMap。
LRU 缓存算法的核心数据结构就是哈希链表,双向链表和哈希表的结合体。这个数据结构长这样
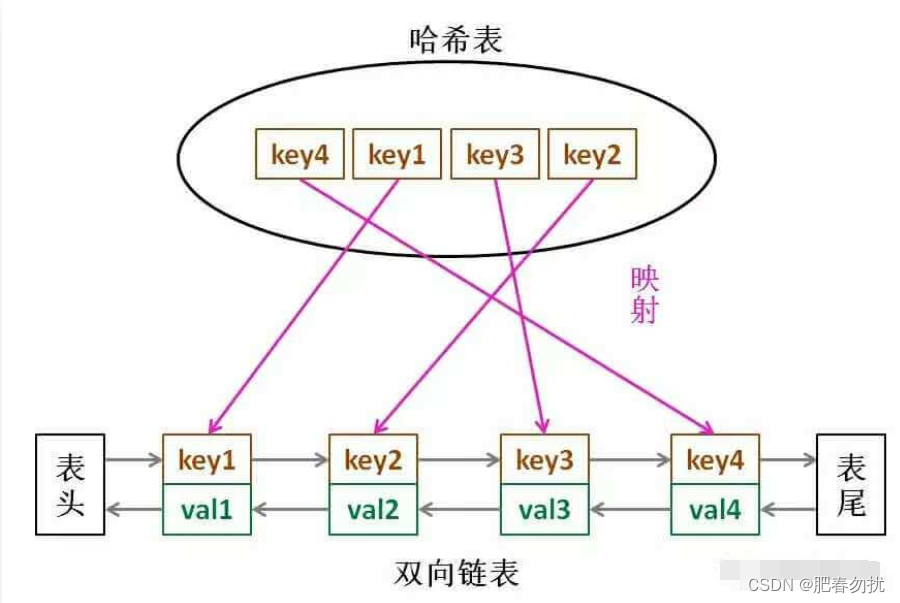
借助这个结构,我们来逐一分析上面的 3 个条件:
1、如果我们每次默认从链表尾部添加元素,那么显然越靠尾部的元素就是最近使用的,越靠头部的元素就是最久未使用的。
2、对于某一个 key,我们可以通过哈希表快速定位到链表中的节点,从而取得对应 val。
3、链表显然是支持在任意位置快速插入和删除的,改改指针就行。只不过传统的链表无法按照索引快速访问某一个位置的元素,而这里借助哈希表,可以通过 key 快速映射到任意一个链表节点,然后进行插入和删除。
三、代码实现
我们把双链表的节点类写出来,为了简化,key 和 val 都认为是 int 类型
class Node {
public int key, val;
public Node next, prev;
public Node(int k, int v) {
this.key = k;
this.val = v;
}
}
然后依靠我们的 Node 类型构建一个双链表,实现几个 LRU 算法必须的 API:
class DoubleList {
// 头尾虚节点
private Node head, tail;
// 链表元素数
private int size;
public DoubleList() {
// 初始化双向链表的数据
head = new Node(0, 0);
tail = new Node(0, 0);
head.next = tail;
tail.prev = head;
size = 0;
}
// 在链表尾部添加节点 x,时间 O(1)
public void addLast(Node x) {
x.prev = tail.prev;
x.next = tail;
tail.prev.next = x;
tail.prev = x;
size++;
}
// 删除链表中的 x 节点(x 一定存在)
// 由于是双链表且给的是目标 Node 节点,时间 O(1)
public void remove(Node x) {
x.prev.next = x.next;
x.next.prev = x.prev;
size--;
}
// 删除链表中第一个节点,并返回该节点,时间 O(1)
public Node removeFirst() {
if (head.next == tail)
return null;
Node first = head.next;
remove(first);
return first;
}
// 返回链表长度,时间 O(1)
public int size() { return size; }
}
为什么必须要用双向链表
因为我们需要删除操作。删除一个节点不光要得到该节点本身的指针,也需要操作其前驱节点的指针,而双向链表才能支持直接查找前驱,保证操作的时间复杂度 O(1)。
注意我们实现的双链表 API 只能从尾部插入,也就是说靠尾部的数据是最近使用的,靠头部的数据是最久未使用的。
有了双向链表的实现,我们只需要在 LRU 算法中把它和哈希表结合起来即可,先搭出代码框架:
class LRUCache {
// key -> Node(key, val)
private HashMap<Integer, Node> map;
// Node(k1, v1) <-> Node(k2, v2)...
private DoubleList cache;
// 最大容量
private int cap;
public LRUCache(int capacity) {
this.cap = capacity;
map = new HashMap<>();
cache = new DoubleList();
}
删除时候既要删除key也要删除node
class LRUCache {
// 为了节约篇幅,省略上文给出的代码部分...
/* 将某个 key 提升为最近使用的 */
private void makeRecently(int key) {
Node x = map.get(key);
// 先从链表中删除这个节点
cache.remove(x);
// 重新插到队尾
cache.addLast(x);
}
/* 添加最近使用的元素 */
private void addRecently(int key, int val) {
Node x = new Node(key, val);
// 链表尾部就是最近使用的元素
cache.addLast(x);
// 别忘了在 map 中添加 key 的映射
map.put(key, x);
}
/* 删除某一个 key */
private void deleteKey(int key) {
Node x = map.get(key);
// 从链表中删除
cache.remove(x);
// 从 map 中删除
map.remove(key);
}
/* 删除最久未使用的元素 */
private void removeLeastRecently() {
// 链表头部的第一个元素就是最久未使用的
Node deletedNode = cache.removeFirst();
// 同时别忘了从 map 中删除它的 key
int deletedKey = deletedNode.key;
map.remove(deletedKey);
}
public int get(int key) {
if (!map.containsKey(key)) {
return -1;
}
// 将该数据提升为最近使用的
makeRecently(key);
return map.get(key).val;
}
public void put(int key, int val) {
if (map.containsKey(key)) {
// 删除旧的数据
deleteKey(key);
// 新插入的数据为最近使用的数据
addRecently(key, val);
return;
}
if (cap == cache.size()) {
// 删除最久未使用的元素
removeLeastRecently();
}
// 添加为最近使用的元素
addRecently(key, val);
}
}