1002 shortest path

记忆化搜索可以用 map 实现,频繁读取而不考虑元素顺序的可以使用 unordered_map ,有效降低时间空间复杂度
dfs(n/2)+n%2+1,其中n%2表示将n变为偶数的次数,1表示操作n/2,dfs(n/2)即表示将n/2变为1的次数
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
unordered_map<ll,int>mp;
ll dfs(ll n){
if(n==0) return 0;
if(n==1) return 0;//从1变为1次数为0
if(mp.count(n)) return mp[n];
return mp[n]=min(dfs(n/2)+n%2+1,dfs(n/3)+n%3+1);
//当n为2时,会出现dfs(0),所以dfs(0)要有返回值,否则就死循环了
//而且当n为2时,n/2合法,但n/3不合法,所以我们要使得dfs(0)的返回值保证取min时取dfs(n/2)+n%2+1而非dfs(n/3)+n%3+1
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--){
ll n;
cin>>n;
cout<<dfs(n)<<endl;
}
return 0;
}或者我们可以先预处理一些f(n),n从1到1e6,当n在这个范围内时,可以直接返回答案
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e6;
int f[N];
unordered_map<ll,int>mp;
ll dfs(ll n){
if(n<N) return f[n];
if(mp.count(n)) return mp[n];
return mp[n]=min(dfs(n/2)+n%2+1,dfs(n/3)+n%3+1);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
memset(f,0x3f,sizeof f);
f[1]=0;//1变为1的次数为0
for(int i=1;i<N;i++){
if(i*2<N) f[i*2]=min(f[i*2],f[i]+1);//f[i*2]可以由f[i]转移过来,操作次数+1,操作为*2
if(i*3<N) f[i*3]=min(f[i*3],f[i]+1);//f[i*3]可以由f[i]转移过来,操作次数+1,操作为*3
if(i+1<N) f[i+1]=min(f[i+1],f[i]+1);//f[i+1]可以由f[i]转移过来,操作次数+1,操作为+1
}
int t=1;
cin>>t;
while(t--){
ll n;
cin>>n;
cout<<dfs(n)<<endl;
}
return 0;
}1005 List Reshape
模拟题
注意cin,cout取消缓冲区同步,不能与getchar()同时用
法一:一个字符一个字符输出,当必要时添加'['或者']'
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<set>
#include<vector>
#include<cstdio>
#define endl '\n'
using namespace std;
typedef long long ll;
string s;
int x,y;
void solve() {
getchar();
getline(cin,s);
cin>>x>>y;
int len=s.size();
int cnt=0;
int cnt1=0;
for(int i=0;i<len;i++){
if(i==1) cout<<'[';
cout<<s[i];
if(s[i+1]==','||s[i+1]==']') cnt++;
else if(s[i]==' ') cnt1++;
if(cnt==y) {
cout<<']';
cnt=0;
}
else if(cnt1==y) {
cout<<'[';
cnt1=0;
}
}
cout<<endl;
}
int main() {
// ios::sync_with_stdio(false);
// cin.tie(0);
// cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}法二:搞一个string类型字符,存储完整的一段字符串,然后放在[]中
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<set>
#include<vector>
#include<cstdio>
#define endl '\n'
using namespace std;
typedef long long ll;
string s;
string ss;
int x,y;
void solve() {
getchar();
getline(cin,s);
cin>>x>>y;
int len=s.size();
cout<<'[';
int cnt=0;
for(int i=1;i<len-1;i++){
char ch=s[i];
ss+=ch;
if(s[i+1]==','||s[i+1]==']') cnt++;
if(cnt==y){
cout<<'['<<ss<<']';
cnt=0;
if(i<len-2) cout<<", ";
i+=2;
ss="";
}
}
cout<<']';
cout<<endl;
}
int main() {
// ios::sync_with_stdio(false);
// cin.tie(0);
// cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}1008 Coins
期望是每次可能结果的概率乘以其结果的总和,可以理解为加权平均,和平均数作对比,n个数的平均数是每个数乘以1/n,然后全部加起来,而加权平均每个数乘以的概率不一样,然后全部加起来
我们先算两个人的数学期望,比如说两个人的硬币数分别为m,n,那么f(m,n)=1+0.5*f(m+1,n-1)+0.5*f(m-1,n+1)
可以这么理解,假设只能是n给m一个硬币,那么f(m,n)=1+1*f(m+1,n-1)
f(m,n)表示第一个有m个硬币,第二个人有n个硬币的回合数,等于下一轮游戏的回合数加1,即1*f(m+1,n-1)+1
只不过算期望回合数需要乘以概率,f(m,n)=1+1*f(m+1,n-1)改成了f(m,n)=1+0.5*f(m+1,n-1)+0.5*f(m-1,n+1)

打表找规律
打表代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
double dfs(ll m,ll n,ll depth){
if(depth==40) return 0;//递归到10层已经很小很小了,接近于0了
if(m==0||n==0) return 0;
return 1+dfs(m+1,n-1,depth+1)/2+dfs(m-1,n+1,depth+1)/2;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
// cin>>t;
while(t--){
ll n,m;
cin>>n>>m;
cout<<dfs(n,m,0)<<endl;
}
return 0;
}


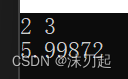
发现f(m,n)=m*n
根据样例

猜测三个人期望回合数为a1*a2+a2*a3+a1*a3
同理,拓展到n个人的情况
由于数据太大,所以用__int128,我们得自己写一个输出函数,否则输出不了__int128类型
a1*a2+a1*a3+...a1*an+a2*a3+...a2*an+a3*a4+...a3*an+...an-1*an=a1*(a2+a3+...an)+a2*(a3+...an)+a3*(a4+...an)+an-1*an
我们可以算出全部的和sum,然后每次求前缀和,用sum减去前缀和就是标蓝的部分
char类型和int类型相加会自动转化为int类型,char类型会先变为它的ascii值,再相加
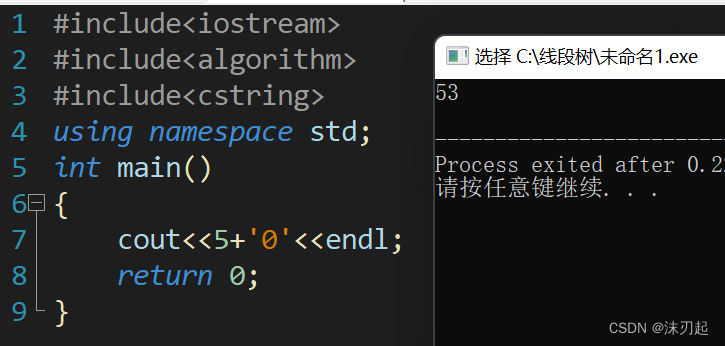
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e5+10;
int a[N];
int n;
inline void print(__int128 x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+'0');
}
void solve() {
cin>>n;
__int128 sum=0;
for(int i=1; i<=n; i++) {
cin>>a[i];
sum+=a[i];
}
__int128 ans=0;
__int128 x=0;
for(int i=1; i<=n; i++) {
x+=a[i];
ans+=a[i]*(sum-x);
}
print(ans);
cout<<endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}