【力扣】42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 *
1
0
4
10^4
104
0 <= height[i] <=
1
0
5
10^5
105
题解
暴力
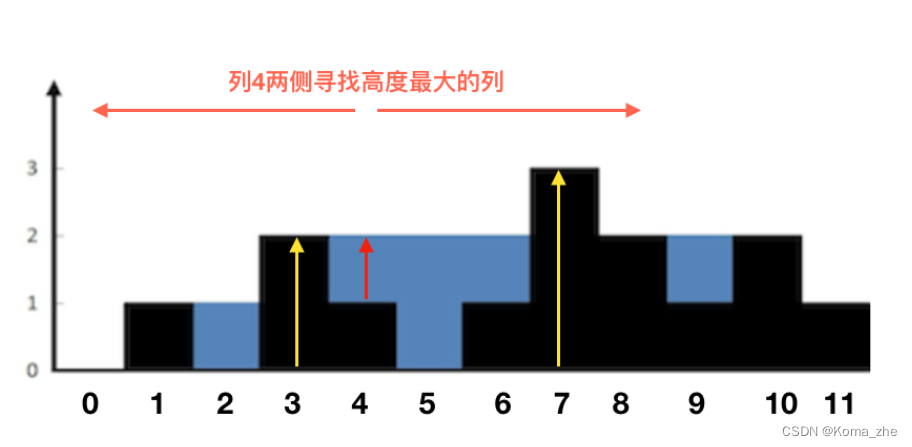
按照列来计算的话,宽度一定是1,把每一列的雨水的高度求出来即可。
每一列雨水的高度,取决于该列左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度
min(lHeight, rHeight) - height
public class Solution {
public int trap(int[] height) {
int sumWater = 0;
for (int i = 0; i < height.length; i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i==0 || i== height.length - 1) {
continue;
}
// 记录右边柱子的最高高度
int rHeight = height[i];
// 记录左边柱子的最高高度
int lHeight = height[i];
// 求左边最高柱子
for (int l = i-1; l >= 0; l--) {
if(height[l] > lHeight) {
lHeight = height[l];
}
}
// 求右边最高柱子
for (int r = i+1; r < height.length; r++) {
if (height[r] > rHeight) {
rHeight = height[r];
}
}
//每一列雨水的高度,取决于,该列左侧最高的柱子和右侧最高的柱子中 最矮的那个柱子的高度。
int h = Math.min(lHeight, rHeight) - height[i];
if (h > 0) {
sumWater += h;
}
}
return sumWater;
}
}
双指针
每到一个柱子都向两边遍历一遍,这其实是有重复计算的,为了得到两边的最高高度,使用了双指针来遍历。把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight),这样就避免了重复计算。
当前位置,左边的最高高度是前一个位置的左边最高高度和本高度的最大值。当前位置,右边的最高高度是前一个位置的右边最高高度和本高度的最大值。
public class Solution {
public int trap(int[] height) {
// 每到一个柱子都向两边遍历一遍,这其实是有重复计算
// 把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight)
int[] maxLeft = new int[height.length];
int[] maxRight = new int[height.length];
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i < height.length; i++) {
//当前位置,左边的最高高度是前一个位置的左边最高高度和本高度的最大值
maxLeft[i] = Math.max(height[i], maxLeft[i - 1]);
}
// 记录每个柱子右边柱子最大高度
maxRight[height.length - 1] = height[height.length - 1];
for (int i = height.length - 2; i >= 0; i--) {
//当前位置,右边的最高高度是前一个位置的右边最高高度和本高度的最大值
maxRight[i] = Math.max(height[i], maxRight[i + 1]);
}
// 求和
int sumWater = 0;
for (int i = 0; i < height.length; i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i==0 || i== height.length - 1) {
continue;
}
int h = Math.min(maxLeft[i], maxRight[i]) - height[i];
if (h > 0) {
sumWater += h;
}
}
return sumWater;
}
}
单调栈
单调栈是按照行方向来计算雨水。
栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
遇到相同高度的柱子:要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。

import java.util.Stack;
public class Solution {
public int trap(int[] height){
int sumWater = 0;
if (height.length <= 2) {
return 0;
}
Stack<Integer> stack = new Stack<>();
stack.push(0);
for (int index = 1; index < height.length; index++){
//情况一
if (height[index] < height[stack.peek()]){
stack.push(index);
}
//情况二
else if (height[index] == height[stack.peek()]){
// 因为相等的相邻墙,左边一个是不可能存放雨水的,所以pop左边的index, push当前的index
stack.pop();
stack.push(index);
}
//情况三
else{
while (!stack.isEmpty() && (height[index] > height[stack.peek()])){
int mid = stack.peek();
stack.pop();
if (!stack.isEmpty()){
int left = stack.peek();
//长就是通过柱子的高度来计算
int h = Math.min(height[left], height[index]) - height[mid];
//宽是通过柱子之间的下标来计算
int w = index - left - 1;
int area = h * w;
if (area > 0) {
sumWater += area;
}
}
}
stack.push(index);
}
}
return sumWater;
}
}