Ubuntu16.04-ros环境搭建笔记=1=

news2024/10/6 5:54:18

tips：搬运资料，留个记录

安装Ubuntu

Ubuntu官网下载地址
安装
虚拟机安装Ubuntu
最好断网安装Ubuntu，可以节约时间
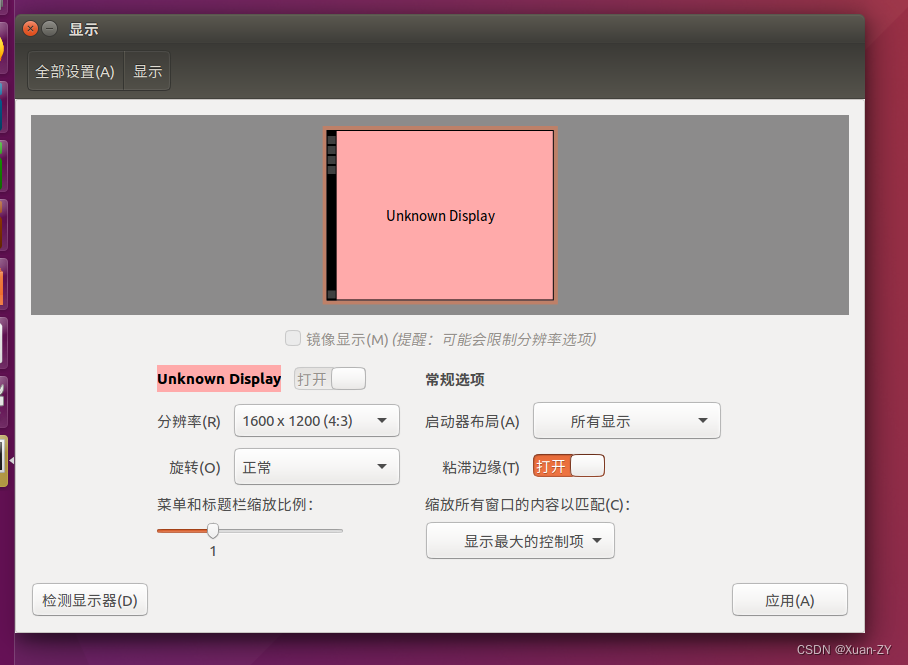
在这里插入图片描述

Ubuntu基础设置

在这里插入图片描述
在这里插入图片描述

Ubuntu换国内源

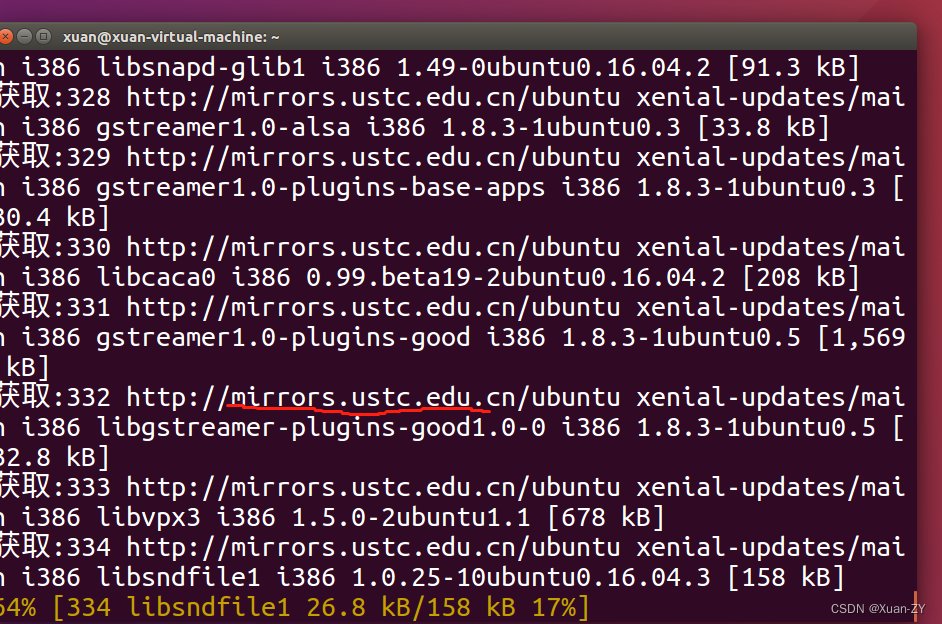
在这里插入图片描述

sudo apt upgrade

可以看到镜像已经换过来了
在这里插入图片描述

VMwareTool安装

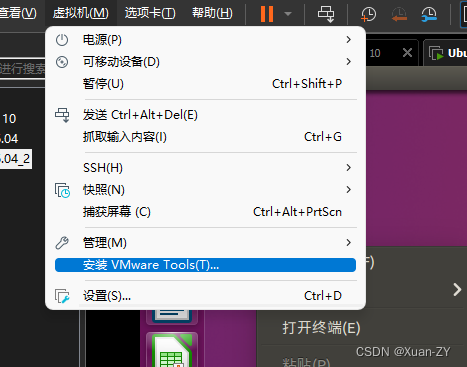
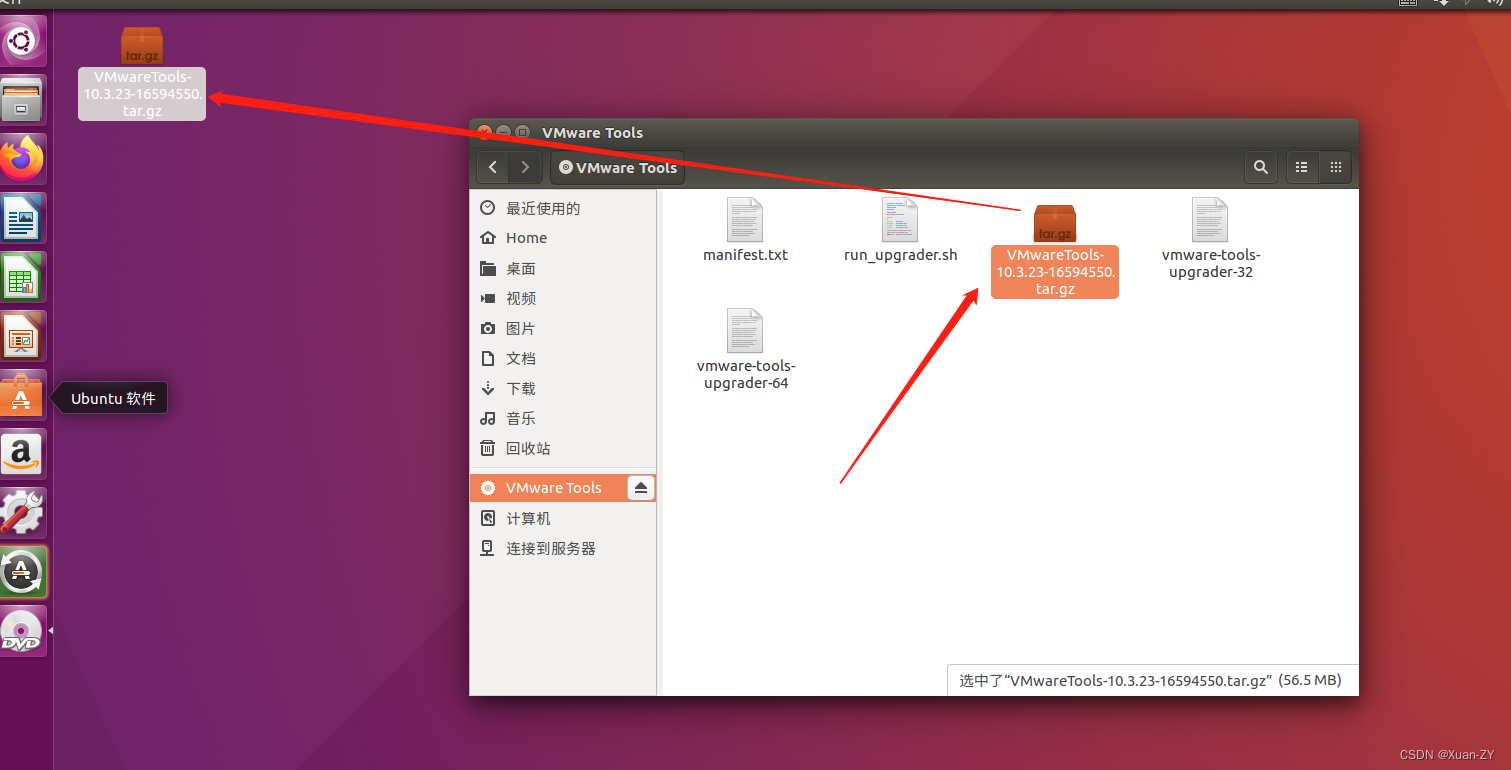
在这里插入图片描述
在这里插入图片描述
把这个压缩包拖到桌面，否则只读文件无法解压
在这里插入图片描述

sudo ./ware-install.pl

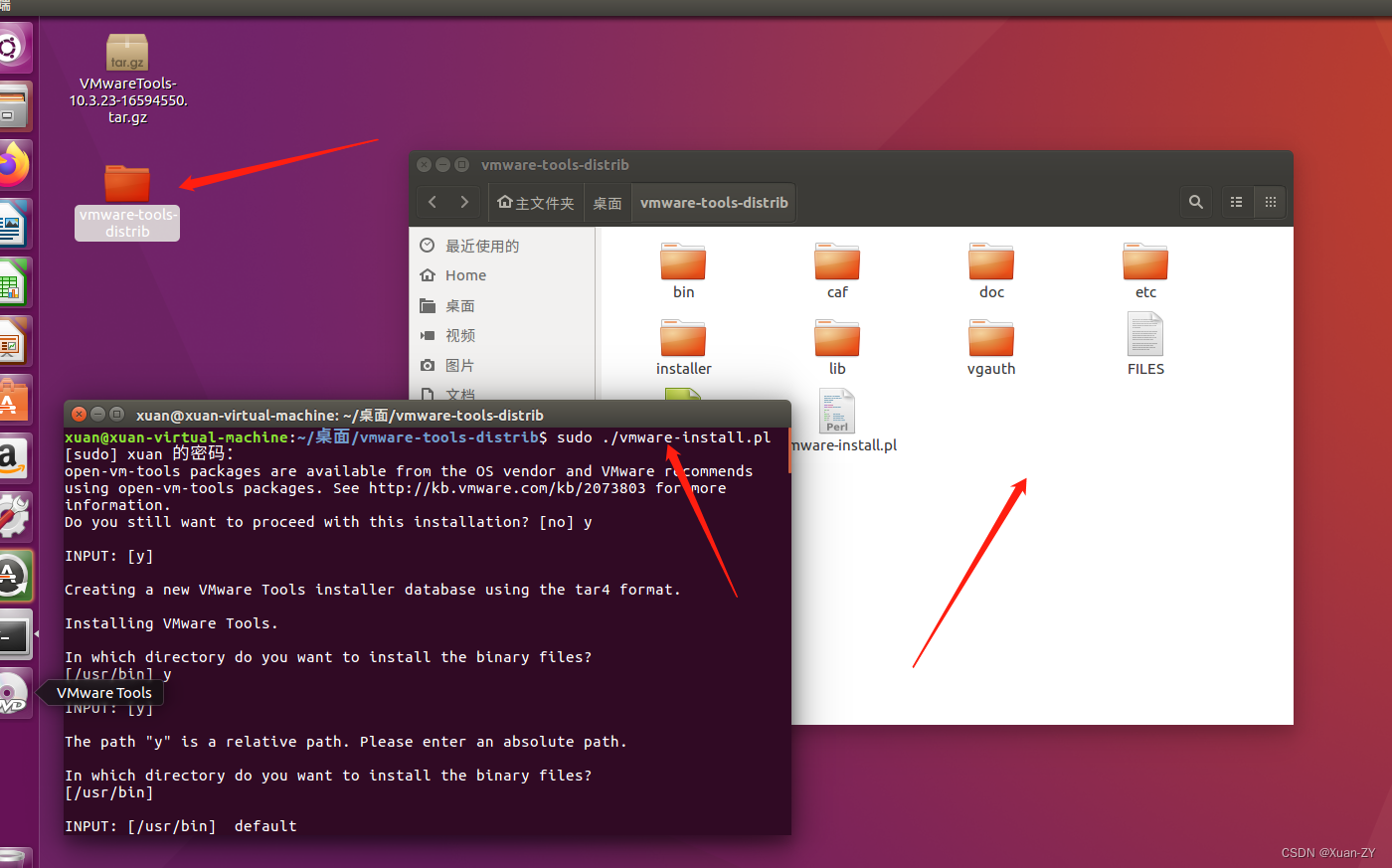
在这里插入图片描述
一路点y就对了
然后关机再开起来就行了

vscode安装

Visual Studio Code（Ubuntu16安装失败amd64报错）

安装python3

安装py3

tips

  1. Ubuntu系统reboot容易出问题，尽量用poweroff
  2. 终端多窗口快捷键：ctrl+shift+t

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/899131.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【以太网通信】RS232 串口转以太网

【以太网通信】RS232 串口转以太网

最近和 RK 研发同事在调试通信接口，排查与定位 RK3399 接收数据出错的问题。FPGA 与 RK3399 之间使用一路 RS232 串口进行通信，由于串口数据没有分包，不方便排查问题，想到可以开发一个 RS232 串口转以太网的工具，将串口…
阅读更多...
【C语言】通讯录（文件） -- 详解

【C语言】通讯录（文件） -- 详解

⚪前言 前面介绍了【C语言】静态通讯录 -- 详解_炫酷的伊莉娜的博客-CSDN博客和【C语言】动态通讯录 -- 详解_炫酷的伊莉娜的博客-CSDN博客。当通讯录运行起来时，可以对通讯录中的数据进行增加、删除或修改等。此时数据是存放在内存中，当程序退出时&…
阅读更多...
不可忽略：冒烟测试到底有多重要？

不可忽略：冒烟测试到底有多重要？

冒烟测试介绍 冒烟测试一词，来源于电路板测试：电路板拼接或组装完成后，进行通电测试，如果冒烟，则说明存在缺陷。 而软件应用中，对其的定义为：在软件开发过程中的一种针对软件版本包的快速基本…
阅读更多...
双亲委派机制，懂吧~ 那什么情况下需要破坏它，知道吗？

双亲委派机制，懂吧~ 那什么情况下需要破坏它，知道吗？

一、什么是双亲委派机制？ 我们要获得一个类的Class实例，可以采用如下方式： 那么在Class的forName(className)方法中，会根据是谁调用了Class.forName(className)这个方法，那么就获得当时加载了它的那个ClassLoader&…
阅读更多...
uniapp选择只选择月份demo效果（整理）

uniapp选择只选择月份demo效果（整理）

<template><view style"margin-top: 200rpx;"><!-- mode"multiSelector" 多列选择器 --><view><picker :range"years" :value"echoVal" change"yearChange" mode"multiSelector">{…
阅读更多...
【面试题】2、Docker和Spring相关

【面试题】2、Docker和Spring相关

1、Docker是什么&#xff1f; &#xff08;1&#xff09;Docker是一个快速交互、运行应用的技术&#xff0c;可以将程序及其依赖、运行环境一起打包为一个镜像&#xff0c;该镜像可以迁移到任意的Linux操作系统 &#xff08;2&#xff09;运行时利用沙箱机制形成隔离容器&…
阅读更多...
【JasperReports笔记04】如何使用Jasper Studio制作父子报表，并且通过Java + Parameters参数填充模板文件

【JasperReports笔记04】如何使用Jasper Studio制作父子报表，并且通过Java + Parameters参数填充模板文件

这篇文章&#xff0c;主要介绍如何使用Jasper Studio制作父子报表&#xff0c;并且通过Java Parameters参数填充模板文件。 目录 一、JasperReports实现父子报表 1.1、运行效果 1.2、制作模板 &#xff08;1&#xff09;制作子报表 &#xff08;2&#xff09;制作子报表的…
阅读更多...
计算机竞赛 图像检索算法

计算机竞赛 图像检索算法

文章目录 1 前言2 图像检索介绍(1) 无监督图像检索(2) 有监督图像检索 3 图像检索步骤4 应用实例5 最后 1 前言 &#x1f525; 优质竞赛项目系列&#xff0c;今天要分享的是 图像检索算法 该项目较为新颖&#xff0c;适合作为竞赛课题方向&#xff0c;学长非常推荐&#xff…
阅读更多...
0101读写分离测试-jdbc-shardingsphere-中间件

0101读写分离测试-jdbc-shardingsphere-中间件

文章目录 1 前言2、创建SpringBoot程序2.1、创建项目2.2、添加依赖2.3、生成实体类、service与Mapper1.5、配置读写分离 2、测试2.1、读写分离测试2.2、事务测试2.3、负载均衡测试 结语 1 前言 shardingshpere-jdbc定位为轻量级 Java 框架&#xff0c;在 Java 的 JDBC 层提供的…
阅读更多...
处理Selenium3+python3定位鼠标悬停才显示的元素

处理Selenium3+python3定位鼠标悬停才显示的元素

这篇文章主要介绍了Selenium3python3--如何定位鼠标悬停才显示的元素 &#xff0c;文中通过简单代码给大家介绍的非常详细,需要的朋友可以参考下 先给大家介绍下Selenium3python3--如何定位鼠标悬停才显示的元素 定位鼠标悬停才显示的元素&#xff0c;要引入新模块 # coding…
阅读更多...
Tableau画图

Tableau画图

目录 蝴蝶图 四象图 排序图 盒型图/散点图 圆环图 火柴图 直方图 瀑布图 地理图 面积图 树地图 面积图 条形图 词云图 双轴图 填充地图 tableau2023.2 须知 蝴蝶图 拉好数据之后 创建新字段正负销售额&#xff0c;并拖入第一个颜色标记卡 四象图 智能推荐 散…
阅读更多...
使用句子嵌入的无监督文本摘要

使用句子嵌入的无监督文本摘要

一、说明 这是一个AI研究生班的作业练习&#xff0c; 在本文中&#xff0c;我将描述我用来在 Python 中执行文本摘要的方法&#xff0c;这是我在导师分配给我的很棒的任务列表之一。 二、什么是文本摘要&#xff1f; 文本摘要是从一个或多个源中提取最重要的信息以生成特定用户…
阅读更多...
华为ENSP网络设备配置实战4（OSPF+BGP+VPN+单臂路由）

华为ENSP网络设备配置实战4（OSPF+BGP+VPN+单臂路由）

题目要求 1、loopback口通过OSPF连通&#xff0c;合理规划OSPF开销&#xff0c;通过设置AR1->AR2->AR4链路&#xff0c;来消除负载链路。 2、AR3、AR4分别与AR1、AR2建立BGP邻居 3、AR3、AR4作为PC机网关设备 4、PC1、PC3由VPN-spi承载&#xff0c;PC2、PC4由VPN-spims承…
阅读更多...
【算法挨揍日记】day03——双指针算法_有效三角形的个数、和为s的两个数字

【算法挨揍日记】day03——双指针算法_有效三角形的个数、和为s的两个数字

611. 有效三角形的个数 611. 有效三角形的个数https://leetcode.cn/problems/valid-triangle-number/ 题目描述&#xff1a; 给定一个包含非负整数的数组 nums &#xff0c;返回其中可以组成三角形三条边的三元组个数。 解题思路&#xff1a; 本题是一个关于三角形是否能成立…
阅读更多...
通过爬虫抓取上市企业利润表并在睿思BI中展示

通过爬虫抓取上市企业利润表并在睿思BI中展示

睿思BI从v5.3开始支持网络爬虫&#xff0c;可以从指定URL抓取表格数据&#xff0c;本示例实现从网络上抓取上市企业招商银行的利润表数据&#xff0c;并在睿思BI中进行展现。 首先&#xff1a;从搜狐财经抓取招商银行利润表数据&#xff0c;操作过程如下&#xff1a; 1.在睿思…
阅读更多...
提示词4大经典框架；将AI融入动画工作流的案例和实践经验；构建基于LLM的系统和产品的模式；提示工程的艺术 | ShowMeAI日报

提示词4大经典框架；将AI融入动画工作流的案例和实践经验；构建基于LLM的系统和产品的模式；提示工程的艺术 | ShowMeAI日报

&#x1f440;日报&周刊合集 | &#x1f3a1;生产力工具与行业应用大全 | &#x1f9e1; 点赞关注评论拜托啦&#xff01; &#x1f916; 高效提示词的4大经典框架&#xff1a;ICIO、CRISPE、BROKE、RASCEF ICIO 框架 Intruction (任务) &#xff1a;你希望AI去做的任务&am…
阅读更多...
软件测试中如何测试算法？

软件测试中如何测试算法？

广义的算法是指解决问题的方案,小到求解数学题,大到制定商业策略,都可以叫做算法。而我们 今天讨论的软件测试中的算法,对应的英文单词为Algorithm ,专指计算机处理复杂问题的程序或 指令。 随着最近几年人工智能等领域的快速发展,算法受到前所未有的重视,算法测试也随之兴起。…
阅读更多...
异步电机IM-改进的电压模型磁链观测器学习

异步电机IM-改进的电压模型磁链观测器学习

导读&#xff1a;本期文章主要介绍异步电机的改进型电压模型磁链观测器。传统纯积分形式的积分器在低速区域存在初始值问题和直流偏置问题&#xff0c;所以在实际应用中必须对电压模型进行改进。本期文章中的对电压模型改进是借鉴一篇IEEE中的方法。 如果需要文章中对应的仿真…
阅读更多...
gcc make cmake ninja的区别

gcc make cmake ninja的区别

理清C编译过程用到的工具概念 ref: 知乎 早先学C的时候&#xff0c;因为只需要点击IDE的运行按钮&#xff0c;程序就可以跑起来&#xff0c;写过最复杂的只不过是几个文件的学生管理系统。 现在要重新拾起C&#xff0c;看的项目和之前的不可同日而语&#xff0c;构建系统也复…
阅读更多...
最优化方法Python计算：牛顿算法

最优化方法Python计算：牛顿算法

设函数 f ( x ) f(\boldsymbol{x}) f(x)&#xff0c; x ∈ R n \boldsymbol{x}\in\text{ℝ}^n x∈Rn二阶连续可微&#xff0c;记 g ( x ) ∇ f ( x ) \boldsymbol{g}(\boldsymbol{x})\nabla f(\boldsymbol{x}) g(x)∇f(x)&#xff0c; H ( x ) ∇ 2 f ( x ) \boldsymbol{H}(\…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023