整个作业一的内容其实就是要自己动手实现一遍Impulse和Shape Matching这两个方法。作业中给的示例场景如下：

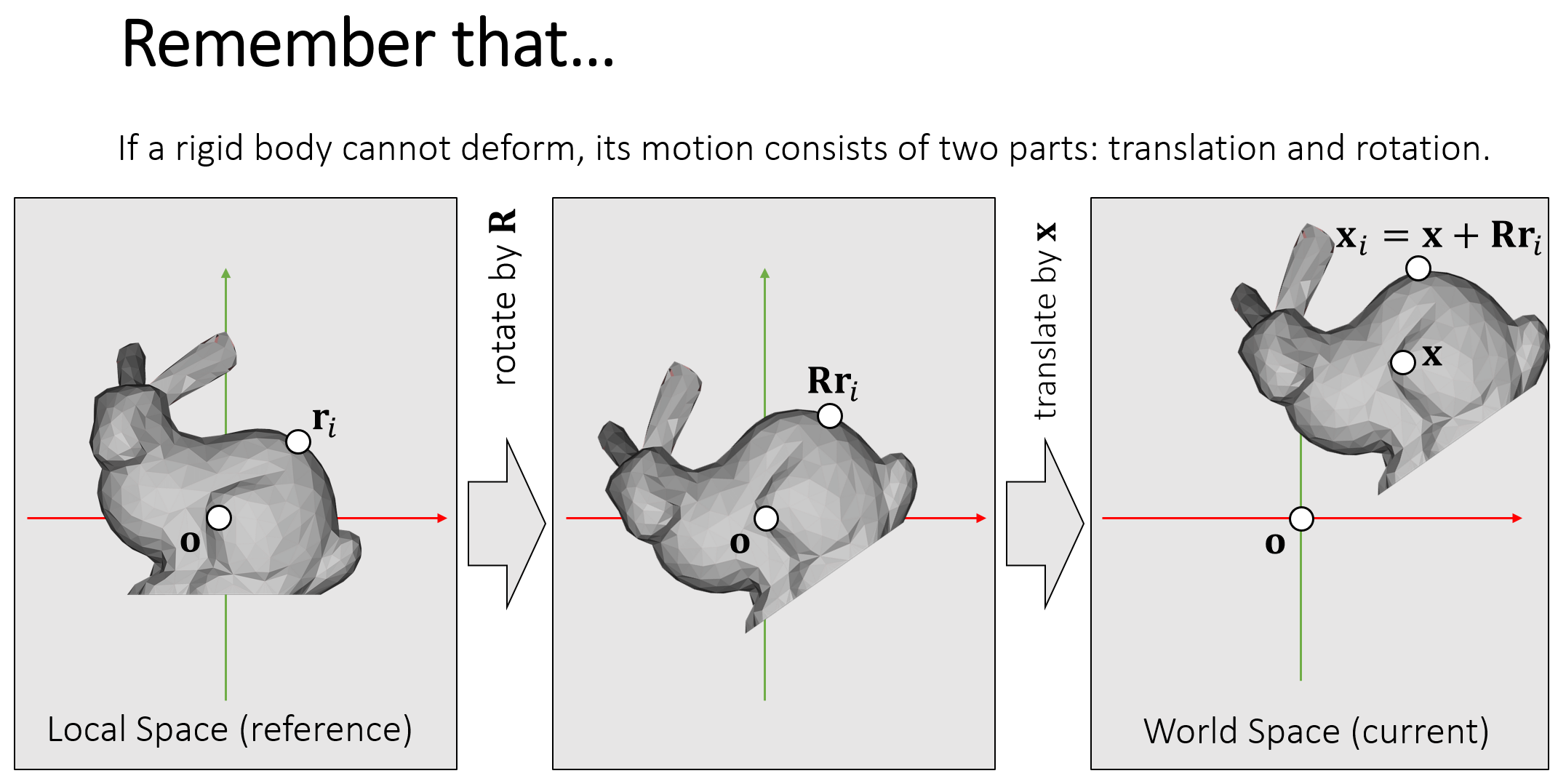
场景中有个兔子的刚体，我们要模拟的就是给兔子一个初始的速度，让其在重力的影响下，与两堵墙发生碰撞的效果。

先看Impulse方法的实现，实现思路就是主要参考PPT中第28页：

首先，我们需要对兔子mesh中的所有顶点进行遍历，找到与墙平面发生碰撞的所有顶点，检查任意顶点是否与墙平面发生碰撞也很简单，就是计算点到平面的距离，若为负值即发生碰撞，也就是PPT中的$\varphi ({\text{x}}_i)<0$：

Mesh mesh = GetComponent<MeshFilter>().mesh;
Vector3[] vertices = mesh.vertices;

Vector3 avg = Vector3.zero;
int num = 0;
for(int i = 0; i < vertices.Length; i++)
{
    Vector3 vert = transform.TransformPoint(vertices[i]);
    if(Vector3.Dot(vert - P, N) < 0)
    {
        avg += vert;
        num++;
    }
}

如果这里得到的num为0，说明所有点都没有和平面发生碰撞，也就不必再继续计算了。下一步，我们计算发生碰撞的点的平均值，作为${\text{x}}_i$，而$\text{R}{\text{r}}_i$其实就是模型中心到这个点的向量：

那么我们就可以得到${\text{v}}_i$，根据速度的方向来判断是否发生碰撞：

avg /= num;

Vector3 rri = avg - transform.position;
Vector3 vi = v + Vector3.Cross(w, rri);
float dot = Vector3.Dot(vi, N);
if(dot >= 0)
{
    return;
}

如果发生碰撞，则需要根据PPT中的公式，更新${\text{v}}_i$：

Vector3 vni = dot * N;
Vector3 vti = vi - vni;
float a = Mathf.Max(1 - u_t * (1 + u_n) * Vector3.Magnitude(vni) / Vector3.Magnitude(vti), 0);
vni = -u_n * vni;
vti = a * vti;
Vector3 vinew = vni + vti;

有了新的${\text{v}}_i$之后，就可以根据它计算出当前的冲量$\text{j}$：

Matrix4x4 inv = Matrix4x4.Inverse(I_ref);
Matrix4x4 k1 = Matrix4x4.identity;
for(int i = 0; i < 4; i++)
{
	k1[i, i] = 1 / mass;
}
Matrix4x4 k2 = Get_Cross_Matrix(rri) * inv * Get_Cross_Matrix(rri);
Matrix4x4 k = new Matrix4x4();
for(int i = 0; i < 4; i++)
{
    for(int j = 0; j < 4; j++)
    {
        k[i, j] = k1[i, j] - k2[i, j];
    }
}

Vector3 J = Matrix4x4.Inverse(k) * (vinew - vi);

进而可以更新刚体的速度$\text{v}$和角速度$\text{w}$：

v = v + J / mass;
Vector3 tmp1 = Vector3.Cross(rri, J);
Vector4 tmp2 = new Vector4(tmp1.x, tmp1.y, tmp1.z, 0);
Vector3 tmp3 = inv * tmp2;
w = w + new Vector3(tmp3.x, tmp3.y, tmp3.z);

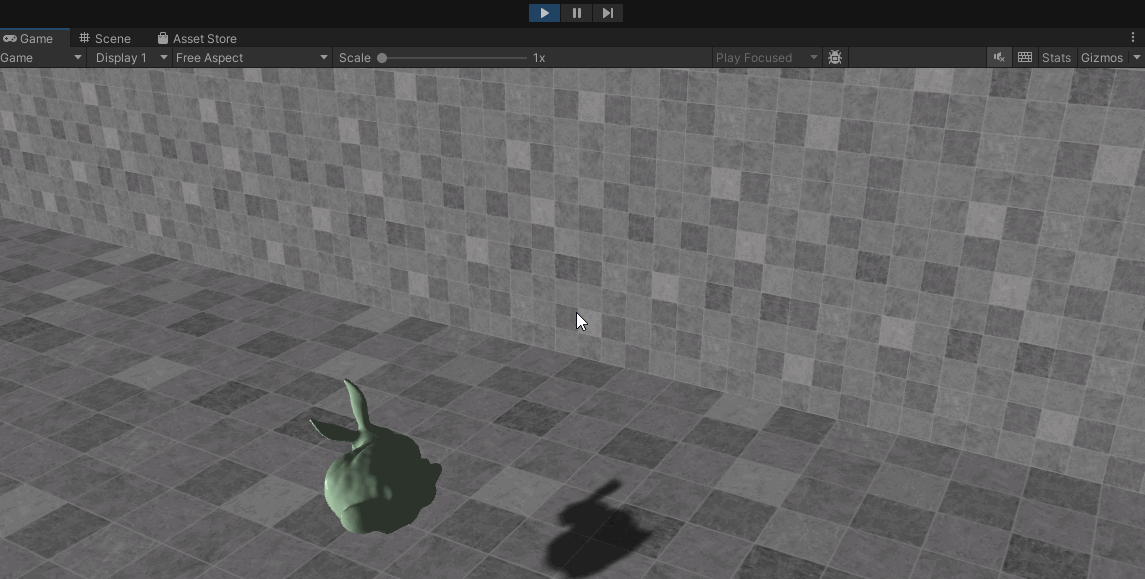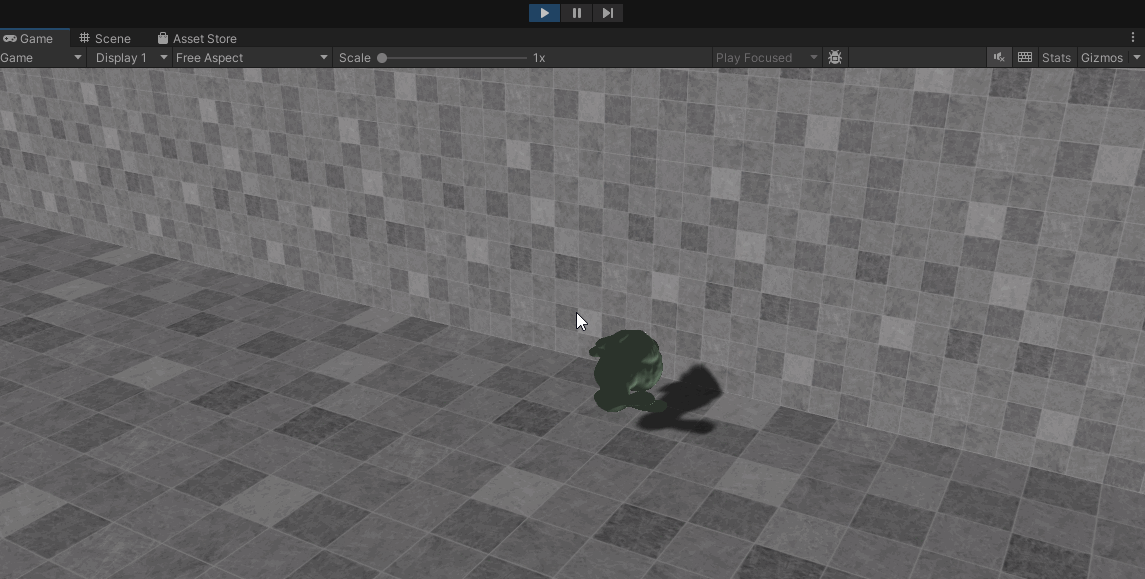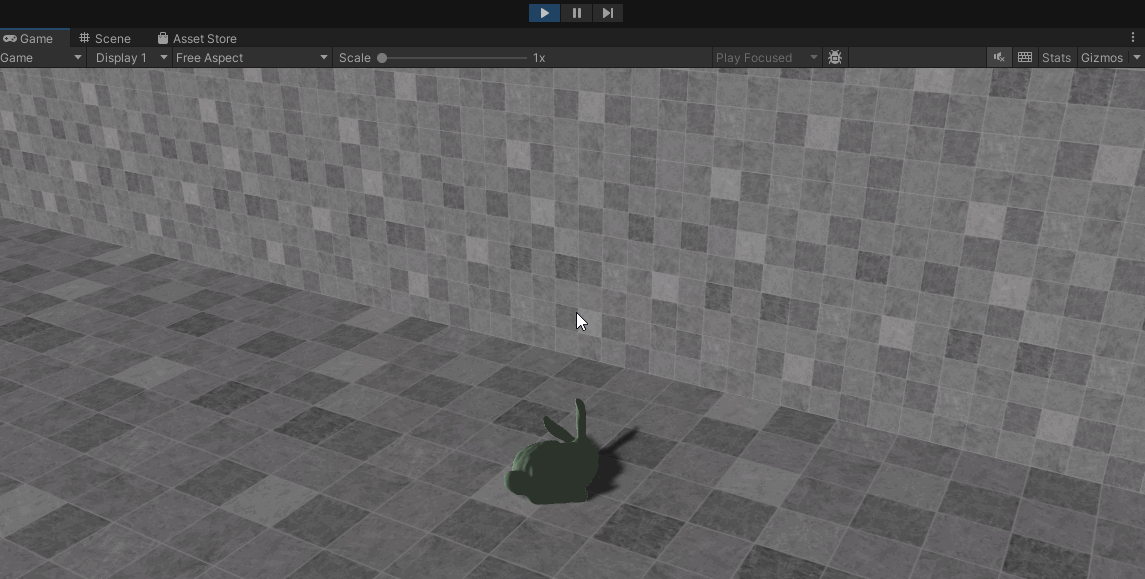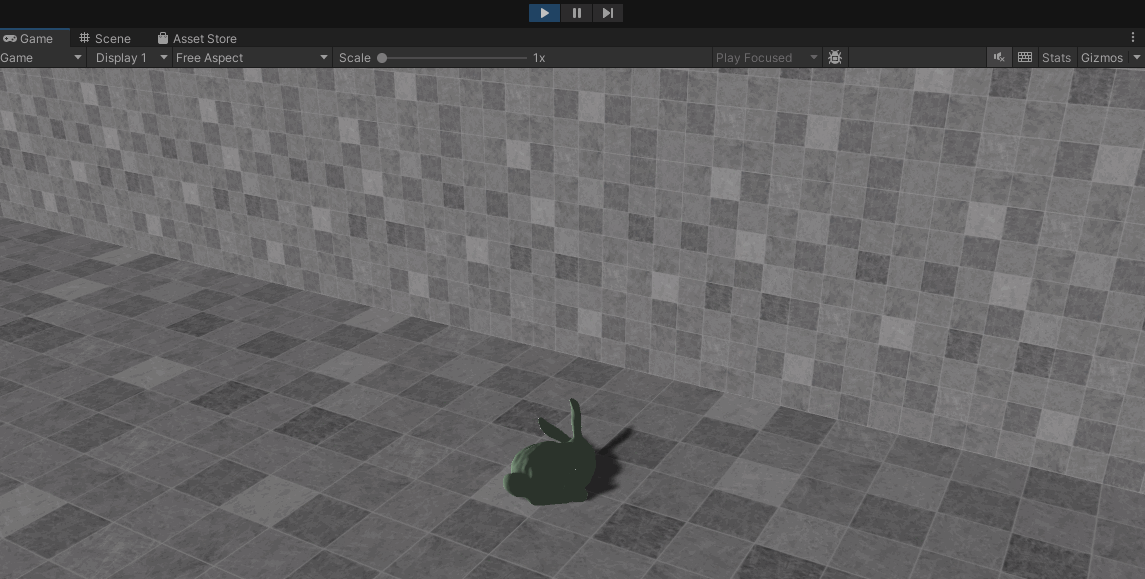
最终就得到了下一时刻刚体的位置和旋转。实现的效果如下：

接下来就是Shape Matching方法了，它的原理就是让每个顶点先分别自由地计算各自的速度和位置，然后再根据刚体的约束，对顶点进行调整，得到每个顶点最终的速度和位置。实现思路也主要参考PPT中第39页：

每个顶点与平面发生碰撞的逻辑依旧可以用Impulse的方法来处理，只不过这里只需要计算出每个顶点碰撞后新的速度${\text{v}}_i$即可：

void Collision(float inv_dt)
{
    for(int i = 0; i < Y.Length; i++)
    {
        Collision_Impulse(i, new Vector3(0, 0.01f, 0), new Vector3(0, 1, 0));
        Collision_Impulse(i, new Vector3(2, 0, 0), new Vector3(-1, 0, 0));
    }
}

更新完位置后，需要计算当前时刻下刚体的中心，以及新的旋转：

Vector3 c=Vector3.zero;
for(int i=0; i<Y.Length; i++)
    c+=Y[i];
c/=Y.Length;
//Shape Matching (translation)
Matrix4x4 A = Matrix4x4.zero;
for(int i=0; i<Y.Length; i++)
{
    Vector3 yic = Y[i] - c;
    A[0, 0]+=yic[0]*Q[i][0];
    A[0, 1]+=yic[0]*Q[i][1];
    A[0, 2]+=yic[0]*Q[i][2];
    A[1, 0]+=yic[1]*Q[i][0];
    A[1, 1]+=yic[1]*Q[i][1];
    A[1, 2]+=yic[1]*Q[i][2];
    A[2, 0]+=yic[2]*Q[i][0];
    A[2, 1]+=yic[2]*Q[i][1];
    A[2, 2]+=yic[2]*Q[i][2];
}
A[3, 3]=1;
A *= Matrix4x4.Inverse(QQt);
//Shape Matching (rotation)
Matrix4x4 R = Get_Rotation(A);

然后，我们再反过来，根据当前的约束去计算每个顶点真正的位置，再和上一时刻的顶点的位置做差，就能得到每个顶点当前时刻的速度了：

void Update_Mesh(Vector3 c, Matrix4x4 R, float inv_dt)
{
    for(int i=0; i<Q.Length; i++)
    {
        Vector3 x=(Vector3)(R*Q[i])+c;

        V[i]=(x-X[i])*inv_dt;
        X[i]=x;
    }
    Mesh mesh = GetComponent<MeshFilter>().mesh;
    mesh.vertices=X;
}

最后运行的效果如下：

如果你觉得我的文章有帮助，欢迎关注我的微信公众号 我是真的想做游戏啊