一、介绍
贝叶斯推理是统计学中的一个主要问题,在许多机器学习方法中也会遇到。例如,用于分类的高斯混合模型或用于主题建模的潜在狄利克雷分配都是在拟合数据时需要解决此类问题的图形模型。
同时,可以注意到,贝叶斯推理问题有时很难解决,具体取决于模型设置(假设、维数等)。在大型问题中,精确的解决方案确实需要大量的计算,而这些计算往往变得难以解决,并且必须使用一些近似技术来克服这个问题并构建快速且可扩展的系统。
在这篇文章中,我们将讨论可用于解决贝叶斯推理问题的两种主要方法:马尔可夫链蒙特卡洛(MCMC),这是一种基于采样的方法,以及变分推理(VI),这是一种基于近似的方法。
二、大纲
在第一部分中,我们将讨论贝叶斯推理问题,并看到一些经典机器学习应用程序的示例,其中自然会出现此问题。然后在第二部分中,我们将介绍全球MCMC技术来解决这个问题,并提供有关两种MCMC算法的一些详细信息:Metropolis-Hasting和Gibbs Sampling。最后,在第三部分中,我们将介绍变分推理,并了解如何在参数化分布族上进行优化过程后获得近似解。
注意。用(∞)标记的小节非常数学,可以跳过而不会损害对这篇文章的全球理解。另请注意,在这篇文章中,p(.) 用于表示概率、概率密度或概率分布,具体取决于上下文。
三、贝叶斯推理问题
在本节中,我们将介绍贝叶斯推理问题并讨论一些计算困难,然后给出潜在狄利克雷分配的例子,这是一种遇到此问题的主题建模的具体机器学习技术。
3.1 什么是推理?
统计推断包括根据我们观察到的内容来了解我们没有观察到的东西。换句话说,它是根据该总体或该总体样本中的一些观察到的变量(通常是效应)得出结论的过程,例如关于总体中某些潜在变量(通常是原因)的准时估计、置信区间或分布估计。
特别是,贝叶斯推理是采用贝叶斯观点产生统计推断的过程。简而言之,贝叶斯范式是一种统计/概率范式,其中每次记录新的观察时,都会更新由概率分布建模的先验知识,其不确定性由另一个概率分布建模。支配贝叶斯范式的整个思想嵌入在所谓的贝叶斯定理中,该定理表达了更新的知识(“后验”),先验知识(“先验”)和来自观察的知识(“可能性”)之间的关系。
一个经典的例子是参数的贝叶斯推理。让我们假设一个模型,其中数据 x 是根据未知参数 θ 从概率分布生成的。我们还假设我们对参数 θ 有先验知识,可以表示为概率分布 p(θ)。然后,当观察到数据 x 时,我们可以使用贝叶斯定理更新有关此参数的先验知识,如下所示
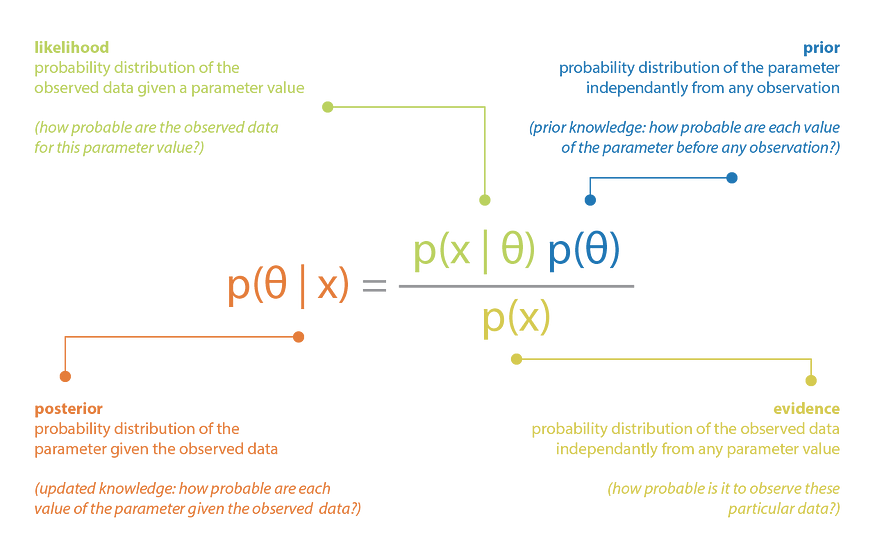
贝叶斯定理应用于给定观测数据的参数推断的图示。
3.2 计算困难
贝叶斯定理告诉我们,后验的计算需要三个项:先验、可能性和证据。前两个可以很容易地表达,因为它们是假设模型的一部分(在许多情况下,先验和可能性是明确已知的)。但是,第三项,即归一化因子,需要计算如下:
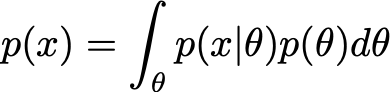
虽然在低维中可以毫不费力地计算这个积分,但在高维中它可能变得棘手。在最后一种情况下,后验分布的精确计算实际上是不可行的,必须使用一些近似技术来获得需要知道该后验的问题的解决方案(例如平均计算)。
我们可以注意到,贝叶斯推理问题可能会产生一些其他计算困难,例如,当某些变量是离散的时,组合数学问题。在最常用于克服这些困难的方法中,我们发现马尔可夫链蒙特卡罗和变分推理方法。在这篇文章的后面,我们将描述这两种方法,特别关注“归一化因子问题”,但应该记住,当面对与贝叶斯推理相关的其他计算困难时,这些方法也很宝贵。
为了使接下来的章节更加通用,我们可以观察到,由于 x 应该被给出并且可以作为参数进行,因此我们面临着这样一种情况:我们在 θ 上定义了一个概率分布,直到一个归一化因子。
![]()
在接下来的两节中描述MCMC和VI之前,让我们举一个使用潜在狄利克雷分配的机器学习中的贝叶斯推理问题的具体示例。
3.3 例
贝叶斯推理问题自然会出现,例如,在假设概率图模型的机器学习方法中,并且给定一些观察结果,我们希望恢复模型的潜在变量。在主题建模中,潜在狄利克雷分配(LDA)方法为语料库中的文本描述定义了这样的模型。因此,给定大小为 V 的完整语料库词汇表和给定数量的主题 T,该模型假设:
- 对于每个主题,词汇表上都存在“主题-词”概率分布(假设先验狄利克雷)
- 对于每个文档,存在主题上的“文档-主题”概率分布(假设另一个狄利克雷先验)
- 文档中的每个单词都经过采样,首先,我们从文档的“文档-主题”分布中抽取了一个主题,其次,我们从附加到采样主题的“主题-单词”分布中抽取了一个单词
该方法的名称来自模型中假设的狄利克雷先验,其目的是推断观察到的语料库中的潜在主题以及每个文档的主题分解。即使我们不深入研究LDA的细节,我们也可以非常粗略地说,表示语料库中单词的向量w和与这些单词相关的主题向量,我们希望根据观察到的w以贝叶斯方式推断z:
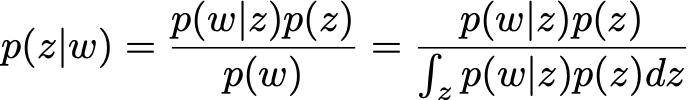
在这里,除了归一化因子由于维度巨大而绝对难以处理这一事实之外,我们还面临着一个组合挑战(因为问题的某些变量是离散的),需要使用MCMC或VI来获得近似解。对主题建模及其特定的潜在贝叶斯推理问题感兴趣的读者可以看看这篇关于LDA的参考论文。
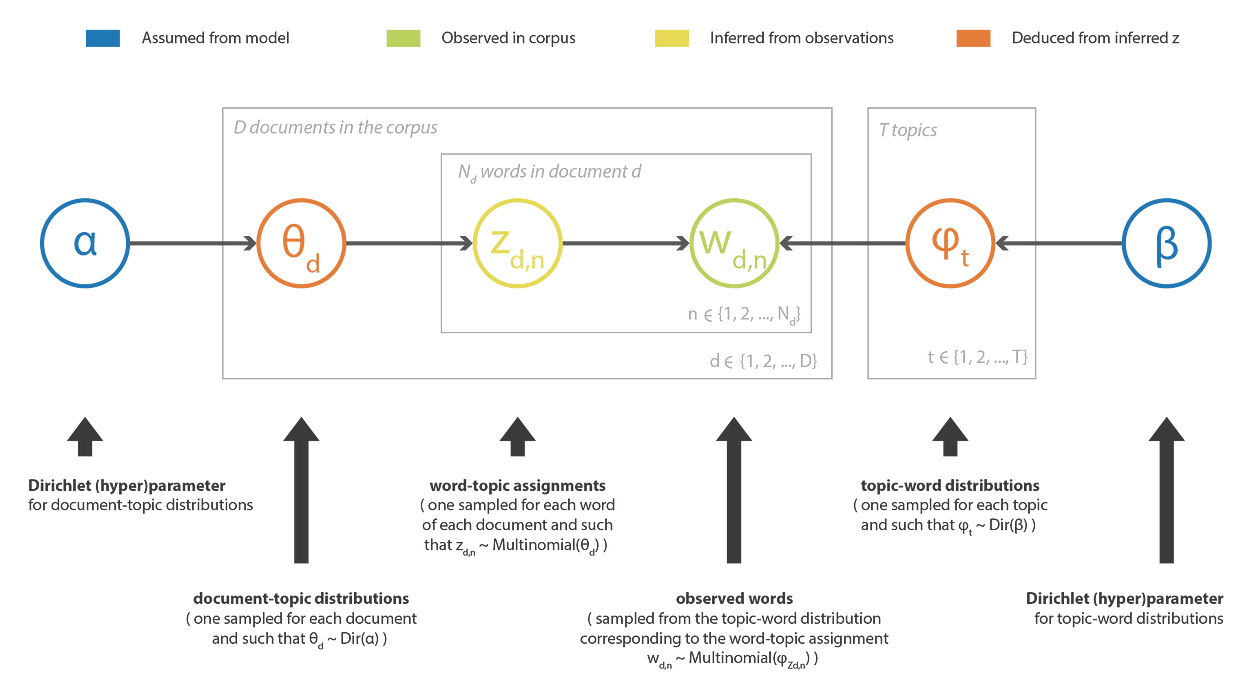
潜在狄利克雷分配方法图示。
四、马尔可夫链蒙特卡洛 (MCMC)
正如我们之前提到的,处理贝叶斯推理问题时面临的主要困难之一来自归一化因子。在本节中,我们描述了MCMC采样方法,这些方法构成了克服此问题的可能解决方案,以及与贝叶斯推理相关的其他一些计算困难。
4.1 抽样方法
抽样方法的思路如下。让我们首先假设我们有一种方法(MCMC)从定义为因子的概率分布中提取样本。然后,我们不必尝试处理涉及后验的棘手计算,而是可以从该分布中获取样本(仅使用未归一化的部分定义),并使用这些样本来计算各种准时统计量,例如均值和方差,甚至通过核密度估计近似分布。
与下一节中描述的VI方法相反,MCMC方法假设所研究的概率分布没有模型(贝叶斯推理案例中的后验)。因此,这些方法具有低偏差但高方差,这意味着大多数时候获得结果的成本更高,但也比我们从VI中获得的结果更准确。
为了结束这一小节,我们再次概述了这样一个事实,即我们刚刚描述的这个抽样过程不限于后验分布的贝叶斯推断,并且更一般地说,还可以用于概率分布定义为其归一化因子的任何情况。

抽样方法(MCMC)的图示。
4.2 MCMC的理念
在统计学中,马尔可夫链蒙特卡罗算法旨在从给定的概率分布中生成样本。该方法名称的“蒙特卡洛”部分是由于采样目的,而“马尔可夫链”部分来自我们获取这些样本的方式(我们请读者参考我们关于马尔可夫链的介绍性文章)。
为了产生样本,我们的想法是建立一个马尔可夫链,其平稳分布是我们想要从中采样的分布。然后,我们可以模拟来自马尔可夫链的随机状态序列,该序列足够长(几乎)达到稳定状态,然后保留一些生成的状态作为我们的样本。
在随机变量生成技术中,MCMC是一种非常先进的方法(我们已经在关于GAN的文章中讨论了另一种方法),它可以从非常困难的概率分布中获取样本,该概率分布可能仅定义到乘法常数。使用MCMC,我们可以从未很好地归一化的分布中获得样本,这是一个违反直觉的事实是,我们定义马尔可夫链的特定方式对这些归一化因子不敏感。
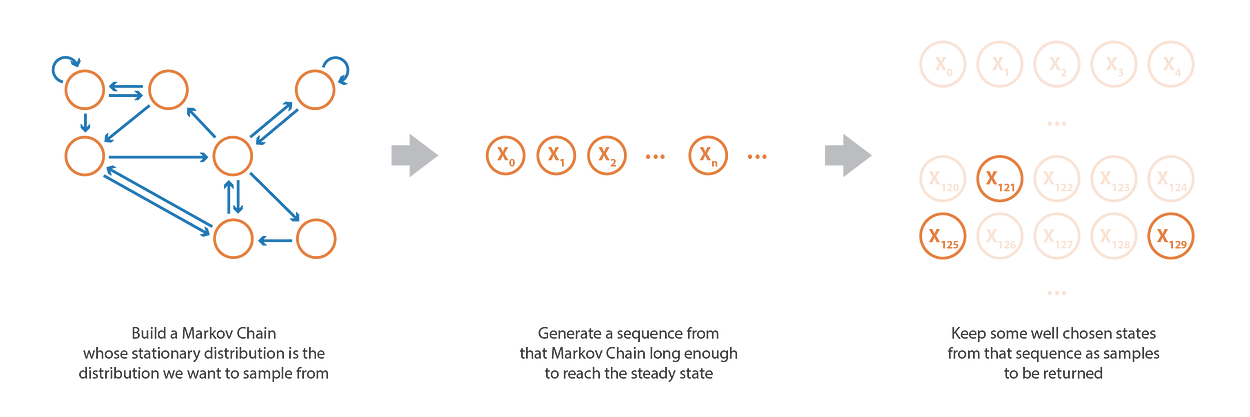
马尔可夫链蒙特卡罗方法旨在从困难的概率分布中生成样本,该概率分布可以定义为一个因子。
4.3 马尔可夫链的定义
整个MCMC方法基于构建马尔可夫链的能力,其平稳分布是我们想要采样的分布。为了做到这一点,Metropolis-Hasting和Gibbs采样算法都使用了马尔可夫链的一个特殊属性:可逆性。
状态空间 E 上的马尔可夫链,转移概率表示为
![]()
如果存在概率分布,则称为可逆γ,使得
![]()
对于这样的马尔可夫链,我们可以很容易地验证我们有

然后,γ是一个平稳分布(如果马尔可夫链是不可约的,则是唯一一个)。
现在让我们假设我们想要从中采样的概率分布π仅定义为一个因子
![]()
(其中 C 是未知乘法常数)。我们可以注意到以下等价性成立

然后,定义转移概率 k(.,.) 以验证最后一个等式的马尔可夫链将如预期的那样π为平稳分布。因此,我们可以定义一个马尔可夫链,对于平稳分布,有一个无法显式计算的概率分布π。
4.4 吉布斯采样过渡 (∞)
假设我们要定义的马尔可夫链是 D 维的,使得
![]()
吉布斯抽样方法基于以下假设:即使联合概率难以处理,也可以计算给定其他维度的单个维度的条件分布。基于这个想法,定义了转换,以便在迭代 n+1 时,要访问的下一个状态由以下过程给出。
首先,我们在 X_n 的 D 维度中随机选择一个整数 d。然后,我们根据相应的条件概率对该维度进行采样,假设所有其他维度都保持固定:
![]()
哪里

是给定所有其他维度的第 d 维的条件分布。
正式地,如果我们表示
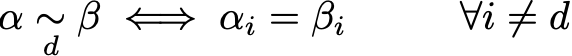
然后可以写入转移概率
因此,对于唯一非平凡的情况,本地余额按预期进行验证,
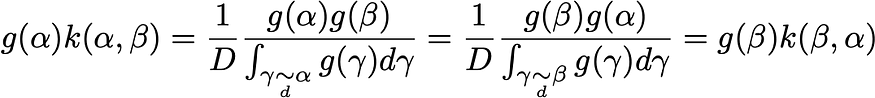
4.5 大都会-黑斯廷过渡(∞)
有时,甚至吉布斯方法中涉及的条件分布也太复杂而无法获得。在这种情况下,可以使用大都会-黑斯廷。为此,我们首先定义一个边转移概率 h(.,.) 用于建议转换。然后,在迭代 n+1 时,马尔可夫链要访问的下一个状态由以下过程定义。我们首先从 h 中绘制一个“建议转换”x,并计算一个相关的概率 r 来接受它:
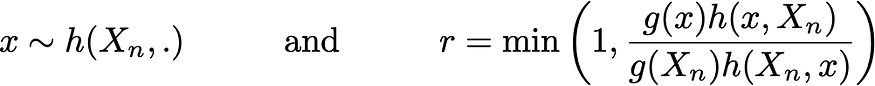
然后选择有效转换,以便
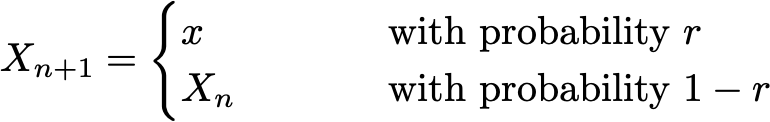
从形式上讲,可以编写转移概率

因此,本地余额按预期验证
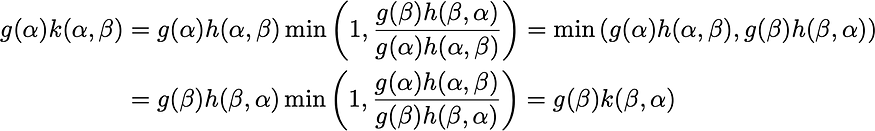
4.6 取样过程
一旦定义了马尔可夫链,我们就可以模拟随机状态序列(随机初始化),并保持其中一些状态的选择,例如获得既遵循目标分布又独立的样本。
首先,为了使样本(几乎)遵循目标分布,我们只需要考虑距离生成序列的开头足够远的状态,以几乎达到马尔可夫链的稳态(稳态,理论上,只是渐近到达)。因此,第一个模拟状态不能用作样本,我们将达到平稳性所需的阶段称为老化时间。请注意,在实践中,很难知道此老化时间必须持续多长时间。
其次,为了拥有(几乎)独立的样本,我们无法在老化时间之后保留序列的所有连续状态。事实上,马尔可夫链定义意味着两个连续状态之间存在很强的相关性,然后我们需要仅将彼此相距足够远的状态作为样本,以被视为几乎独立。在实践中,可以通过分析自相关函数(仅适用于数值)来估计两个状态之间几乎独立的滞后。
因此,为了获得遵循目标分布的独立样本,我们保留了生成序列中的状态,这些状态由滞后 L 彼此隔开,并且在老化时间 B 之后出现。因此,如果表示马尔可夫链的连续状态
![]()
我们只保留状态作为我们的样本
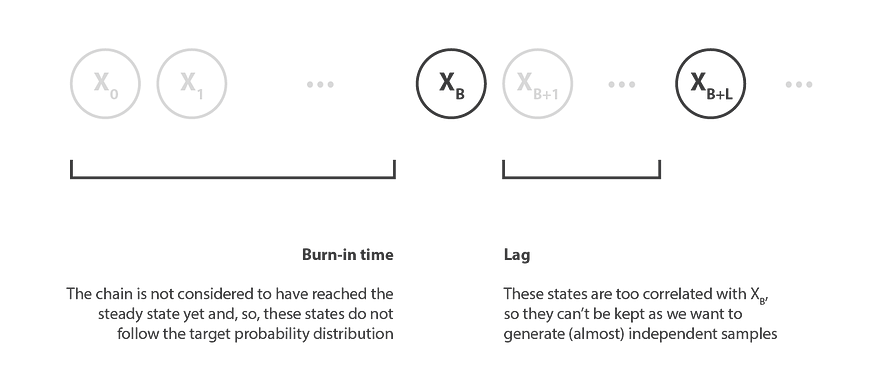
MCMC采样需要考虑老化时间和滞后。
五、变分推理(六)
克服与推理问题相关的计算困难的另一种可能方法是使用变分推理方法,该方法包括找到参数化族中分布的最佳近似值。为了找到这个最佳近似值,我们遵循一个优化过程(基于族参数),只需要定义目标分布到一个因子。
5.1 近似方法
VI方法包括搜索给定族中某些复杂目标概率分布的最佳近似。更具体地说,这个想法是定义一个参数化的分布族,并对参数进行优化,以获得相对于明确定义的误差度量最接近目标的元素。
我们仍然考虑将概率分布π定义为归一化因子 C:
![]()
然后,用更数学的术语来说,如果我们表示分布的参数族
![]()
我们考虑两个分布 p 和 q 之间的误差度量 E(p,q),我们搜索最佳参数,使得

如果我们可以在不必显式归一化π的情况下解决这个最小化问题,我们可以使用 f_ω* 作为近似值来估计各种量,而不是处理棘手的计算。变分推理方法所隐含的优化问题实际上应该比直接计算(归一化、组合数学等)的问题更容易处理。
与抽样方法相反,假设一个模型(参数化族),这意味着偏差,但也意味着较低的方差。一般来说,VI方法不如MCMC方法准确,但产生结果的速度要快得多:这些方法更适合大规模,非常统计的问题。
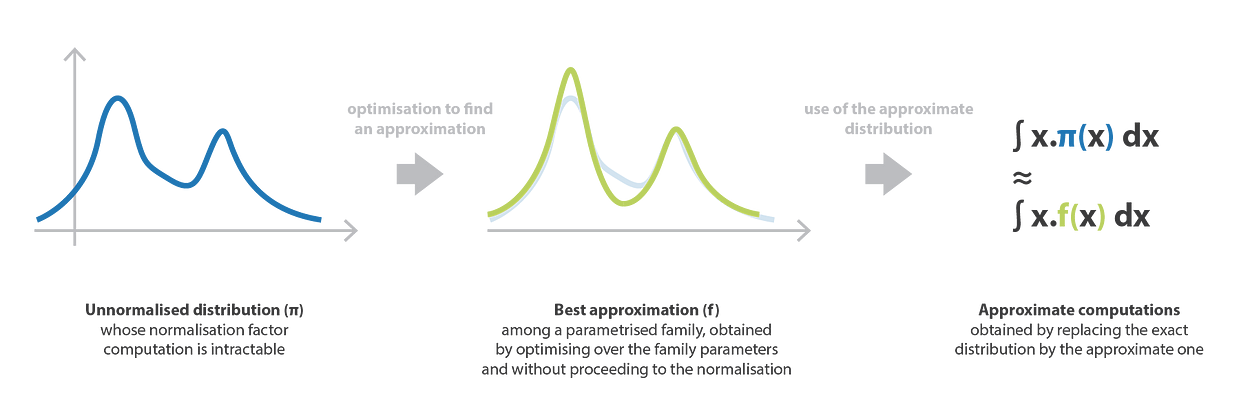
近似方法(变分推理)的图解。
5.2 分布家族
我们需要设置的第一件事是参数化分布族,它定义了我们搜索最佳近似的空间。
系列的选择定义了一个控制方法偏差和复杂性的模型。如果我们假设一个非常严格的模型(简单家族),那么我们就会有很高的偏差,但优化过程很简单。相反,如果我们假设一个相当自由的模型(复杂家族),偏差要低得多,但优化会更难(如果不是难以处理的话)。因此,我们必须在复杂到足以确保最终近似质量的族和足够简单的族之间找到适当的平衡,以使优化过程易于处理。我们应该记住,如果家族中没有分布接近目标分布,那么即使是最好的近似也会给出糟糕的结果。
均场变分族是一系列概率分布,其中所考虑的随机向量的所有分量都是独立的。该系列的分布具有产品密度,因此每个独立组件都由产品的不同因子控制。因此,属于均场变分族的分布具有可以写的密度
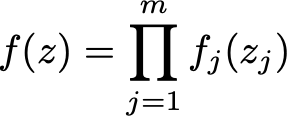
其中我们假设了一个 m 维随机变量 z。请注意,即使在表示法中省略了它,所有密度f_j都是参数化的。因此,例如,如果每个密度f_j都是具有均值和方差参数的高斯,则全局密度 f 由来自所有独立因子的一组参数定义,并且对整组参数进行优化。
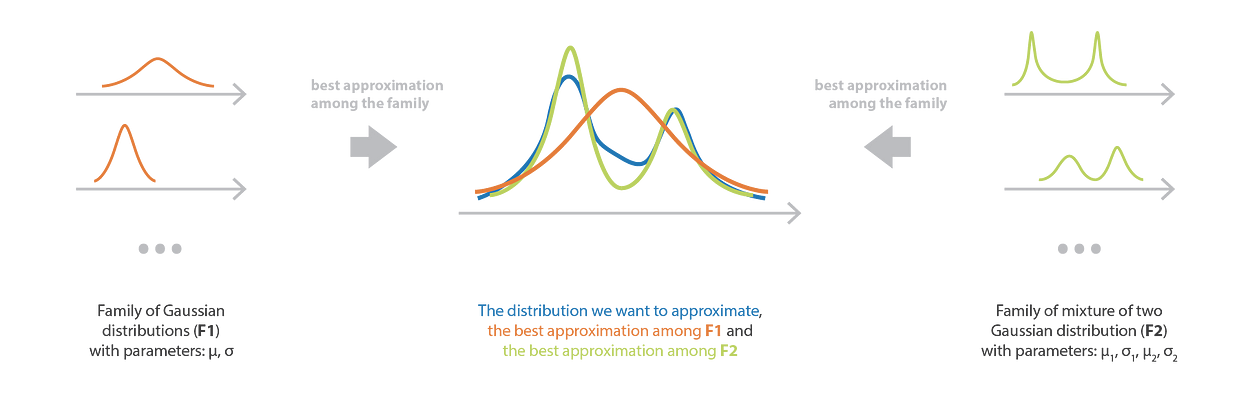
变分推理中族的选择既决定了优化过程的难度,也决定了最终近似的质量。
5.3 库尔巴克-莱布勒背离
一旦定义了族,一个主要问题仍然存在:如何在这个族中找到给定概率分布的最佳近似值(明确定义为其归一化因子)?即使最佳近似显然取决于我们考虑的误差度量的性质,假设最小化问题不应该对归一化因子敏感似乎是很自然的,因为我们想比较质量分布而不是质量本身(对于概率分布必须是单一的)。
因此,现在让我们定义Kullback-Leibler(KL)背离,并看到该度量使问题对归一化因子不敏感。如果 p 和 q 是两个分布,则 KL 散度定义如下
![]()
从这个定义中,我们可以很容易地看到我们有
![]()
这意味着我们的最小化问题的以下相等性
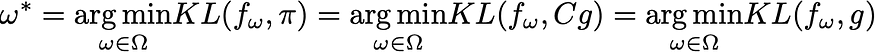
因此,当选择KL散度作为我们的误差度量时,优化过程对乘法系数不敏感,我们可以在参数化分布族中搜索最佳近似值,而不必像预期的那样计算目标分布的痛苦归一化因子。
最后,作为一个附带事实,我们可以通过向感兴趣的读者注意KL散度是交叉熵减去熵来结束这一小节,并且在信息论中有一个很好的解释。
5.4 优化过程和直觉
一旦定义了参数化族和误差度量,我们就可以初始化参数(随机或根据明确定义的策略)并继续进行优化。可以使用几种经典的优化技术,例如梯度下降或坐标下降,在实践中,这将导致局部最优。
为了更好地理解这个优化过程,让我们举一个例子,回到贝叶斯推理问题的具体案例,我们假设一个后验,使得
![]()
在这种情况下,如果我们想使用变分推理获得该后验的近似值,我们必须求解以下优化过程(假设参数化族定义并将KL散度作为误差度量)
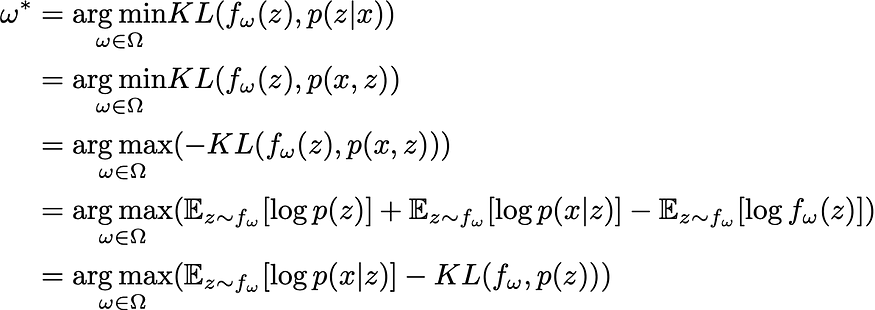
最后一个等式有助于我们更好地理解如何鼓励近似来分配其质量。第一项是预期对数似然,它倾向于调整参数,以便将近似的质量放在潜在变量 z 的值上,这些值可以最好地解释观测数据。第二项是近似和先验之间的负KL散度,它倾向于调整参数以使近似接近先验分布。因此,这个目标函数很好地表达了通常的先验/似然平衡。
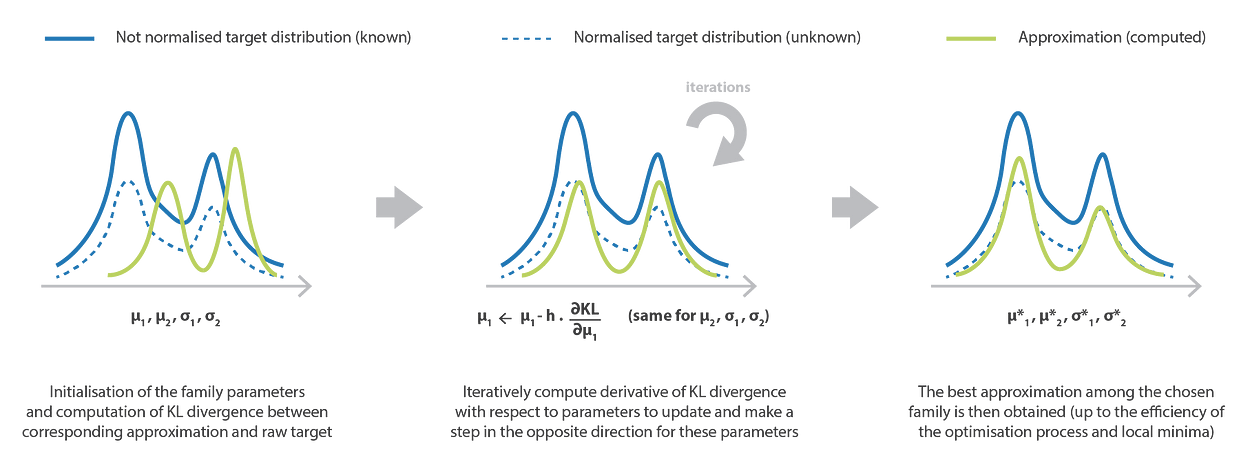
变分推理方法的优化过程。
六、总结
本文的主要内容是:
- 贝叶斯推理是统计学和机器学习中一个非常经典的问题,它依赖于众所周知的贝叶斯定理,其主要缺点在于大多数时候,在一些非常繁重的计算中。
- 马尔可夫链蒙特卡罗(MCMC)方法旨在模拟密度的样品,这些密度可能非常复杂和/或定义到一个因子
- MCMC可用于贝叶斯推理,以便直接从后验的“未归一化部分”生成要使用的样本,而不是处理棘手的计算
- 变分推理 (VI) 是一种近似分布的方法,它使用参数优化过程来找到给定族中的最佳近似
- VI优化过程对目标分布中的乘法常数不敏感,因此,该方法可用于近似定义到归一化因子的后验
如前所述,MCMC和VI方法具有不同的属性,这意味着不同的典型用例。一方面,MCMC方法的采样过程非常繁重,但没有偏差,因此,当预期获得准确的结果时,这些方法是首选,而不考虑所需的时间。另一方面,尽管VI方法中系列的选择可能会明显引入偏差,但它伴随着合理的优化过程,使这些方法特别适用于需要快速计算的非常大规模的推理问题。
MCMC和VI之间的其他比较可以在优秀的变分推理:统计学家评论中找到,我们也强烈推荐给仅对VI感兴趣的读者。有关MCMC的进一步阅读,我们建议使用此一般介绍以及此面向机器学习的介绍。有兴趣了解有关应用于LDA的吉布斯采样的更多信息的读者可以参考这个关于主题建模和吉布斯采样的教程(结合这些关于LDA Gibbs采样器的讲义,以便谨慎推导)。
最后,让我们以一点点调侃来结束,并提到在下一篇文章中,我们将讨论变分自动编码器,这是一种基于变分推理的深度学习方法......敬请期待!约瑟夫·罗卡