pandas计算相关系数
在数据分析和统计学中,相关系数是一种用于衡量两个变量之间关系强度的统计指标。它可以帮助我们了解两个变量之间的线性关系强度和方向。
Pandas是一个强大的Python库,提供了许多用于数据分析和处理的功能。在本文中,我们将介绍如何使用Pandas计算相关系数以及其原理。
导入pandas和数据
首先,我们需要导入Pandas库,用来分析我们的数据。
假设我们有一个包含5个变量X和Y的数据集,我们可以使用sklearn.datasets的make_regression函数生成我们需要的数据。
以下是获取数据的示例代码:
import pandas as pd
# 用sklearn制作一些数据
from sklearn.datasets import make_regression
X, y = make_regression(n_samples=100, n_features=5, noise=1, random_state=42)
df = pd.DataFrame(data=X,columns=list("abcde"))
df["y"] = y

计算相关系数
接下来,我们可以使用Pandas的corr函数计算相关系数。corr函数可以计算多个变量之间的相关系数,返回一个相关系数矩阵。
以下是计算相关系数的示例代码:
# 计算相关系数
corr = df.corr()
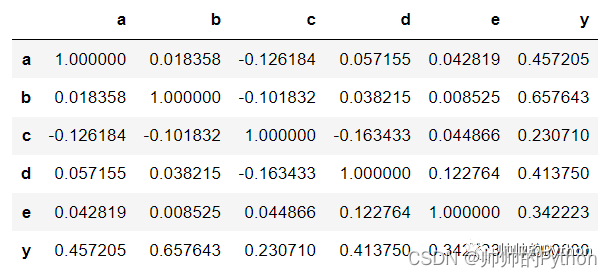
相关系数矩阵是一个对称矩阵,其中每个元素表示两个变量之间的相关系数。对角线上的元素始终为1,因为每个变量与自身的相关系数为1。
相关系数矩阵美化
相关系数矩阵计算完成后,我们可以知道各个变量之间的强弱关系。但是由于数据太多,让人眼花缭乱的看不清楚。我们可以用pandas的表格美化工具,将相关系数低于-0.2和高于0.2的数据标红。
以下是表格数据标红的示例代码:
def highlight_max(s, props=''):
return np.where((s >= 0.2)|(s<=-0.2), props, '')
corr2.style.apply(highlight_max, props='color:white;background-color:red', axis=0)
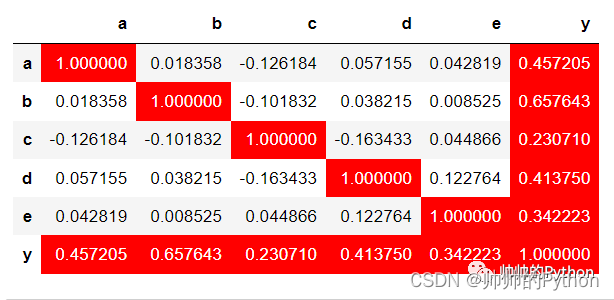
热力图可视化
我们还可以使用seaborn的heatmap函数可视化相关系数矩阵。heatmap函数可以根据相关系数的大小,将相关系数矩阵绘制为热力图。以下是绘制热力图的示例代码:
import warnings
warnings.filterwarnings("ignore")
from pylab import mpl
import matplotlib.pyplot as plt
import seaborn as sns
# 防止中文显示为方格
mpl.rcParams['font.sans-serif']=['SimHei']
f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(corr2,square = True, annot=True, vmax=1,cmap='coolwarm')
plt.show()
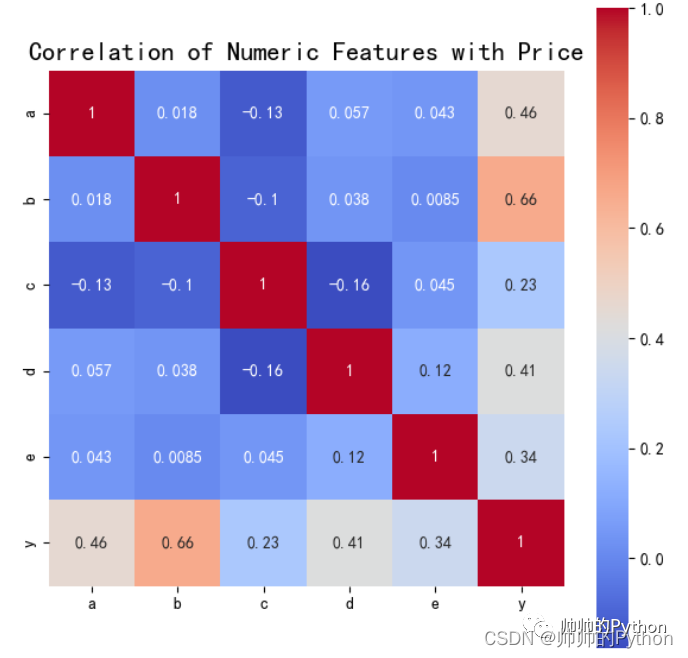
在上述代码中,我们使用seaborn库的heatmap函数绘制热力图,并使用matplotlib库的plt.show()函数显示图形。通过设置annot参数为True,可以在热力图上显示相关系数的值。通过设置cmap参数为coolwarm,可以将相关系数的值映射为不同的颜色。
通过以上步骤,我们可以使用Pandas轻松计算相关系数并可视化相关系数矩阵。这对于分析两个变量之间的关系非常有用,并可以帮助我们了解数据集的特征。
1. 相关系数的定义
相关系数是一个介于-1和1之间的值,表示两个变量之间的关联程度。相关系数为正表示两个变量呈正相关关系,即当一个变量增加时,另一个变量也增加;相关系数为负表示两个变量呈负相关关系,即当一个变量增加时,另一个变量减少;相关系数接近于0表示两个变量之间没有线性关系。
2. 相关系数的计算方法
常用的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。
2.1 皮尔逊相关系数
皮尔逊相关系数是用来衡量两个连续变量之间线性关系强度的统计量。它的计算公式如下:
r = ∑ ( X i − X ˉ ) ( Y i − Y ˉ ) ∑ ( X i − X ˉ ) 2 ∑ ( Y i − Y ˉ ) 2 r = \frac{{\sum{(X_i - \bar{X})(Y_i - \bar{Y})}}}{{\sqrt{\sum{(X_i - \bar{X})^2}\sum{(Y_i - \bar{Y})^2}}}} r=∑(Xi−Xˉ)2∑(Yi−Yˉ)2∑(Xi−Xˉ)(Yi−Yˉ)
其中, X i X_i Xi和 Y i Y_i Yi分别表示两个变量的观测值, X ˉ \bar{X} Xˉ和 Y ˉ \bar{Y} Yˉ分别表示两个变量的均值。
2.2 斯皮尔曼相关系数
斯皮尔曼相关系数是用来衡量两个变量之间的单调关系强度的统计量。它的计算公式如下:
ρ = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) \rho = 1 - \frac{{6\sum{d_i^2}}}{{n(n^2-1)}} ρ=1−n(n2−1)6∑di2
其中, d i d_i di表示两个变量的秩次差, n n n表示样本数量。
3. 相关系数的解释
相关系数的取值范围为-1到1,可以根据取值范围来解释两个变量之间的关系强度和方向。当相关系数接近于1时,表示两个变量之间存在强正相关关系;当相关系数接近于-1时,表示两个变量之间存在强负相关关系;当相关系数接近于0时,表示两个变量之间没有线性关系。
需要注意的是,相关系数只能衡量线性关系,不能衡量非线性关系。此外,相关系数只能衡量两个变量之间的关系,不能确定因果关系。
4. 相关系数的应用
相关系数在统计学和数据分析中有广泛的应用。它可以帮助我们了解变量之间的关系,从而进行预测和决策。
在金融领域,相关系数可以用来衡量不同股票之间的关联程度,从而进行投资组合的优化。
在医学研究中,相关系数可以用来衡量药物剂量与疗效之间的关系,从而确定最佳的治疗方案。
在市场营销中,相关系数可以用来衡量广告投入与销售额之间的关系,从而确定最有效的营销策略。
结论
相关系数是衡量两个变量之间关联程度的重要统计量。通过pandas计算相关系数,我们可以了解两个变量之间的线性关系强度和方向。相关系数的应用广泛,可以帮助我们进行预测和决策。然而,需要注意的是,相关系数只能衡量线性关系,不能确定因果关系。