参考代码:slowtv_monodepth
这篇文章提出了一种在无标定数据集上自监督估计深度的方法,也就是通过网络预测的方式估计相机的内参,从而完成自监督流程。为了验证在无相机标定情况下实现自监督深度估计,从网络上下载了一些视频构建SlowTV数据集,并且一些trick也添加到深度自监督流程中,如对图像做任意长宽比例数据增广。
损失函数:
这里的损失函数与MonoDepth2中的损失函数近似,光度重构误差还是老配方:
L
p
h
(
I
,
I
′
)
=
λ
1
−
L
s
s
i
m
(
I
,
I
′
)
2
+
(
1
−
λ
)
L
I
(
I
,
I
′
)
L_{ph}(I,I^{'})=\lambda\frac{1-L_{ssim}(I,I^{'})}{2}+(1-\lambda)L_I(I,I^{'})
Lph(I,I′)=λ21−Lssim(I,I′)+(1−λ)LI(I,I′)
对于运动目标的处理这里采用前后帧最小重构误差和Auto-Mask机制去缓解(并不能根本上去除):
L
r
e
c
=
∑
p
min
k
L
p
h
(
I
k
,
I
t
+
k
′
)
L_{rec}=\sum_p\min_kL_{ph}(I_k,I^{'}_{t+k})
Lrec=p∑kminLph(Ik,It+k′)
其中,
t
+
k
t+k
t+k是前后帧的索引值。Auto-Mask与之前论文中一致(理论上重构之后的误差应该小于帧间误差):
M
=
[
min
k
L
p
h
(
I
k
,
I
t
+
k
′
)
<
min
k
L
p
h
(
I
k
,
I
t
+
k
)
]
\mathcal{M}=[\min_kL_{ph}(I_k,I^{'}_{t+k})\lt \min_kL_{ph}(I_k,I_{t+k})]
M=[kminLph(Ik,It+k′)<kminLph(Ik,It+k)]
相机内参预测:
由于网络采集的视频没有提供标定的内参数据(对于那些内参准确的场景就没有必要了),因而需要使用网络去预测,对于输入的一个序列只需要一次预测就好了(这部分在代码里面也做了判断),而对于预测部分使用全连阶层预测,只不过对于焦距和中心在输出的时候采用了不同的激活函数,对于焦距预测采用了类似ReLU曲线的Softplus激活函数
# src/networks/pose.py#L86
def _get_focal_dec(self, n_ch: int) -> nn.Sequential:
"""Return focal length estimation decoder. (b, c, h, w) -> (b, 2)"""
return nn.Sequential(
self.block(n_ch, n_ch, kernel_size=3, stride=1, padding=1),
self.block(n_ch, n_ch, kernel_size=3, stride=1, padding=1),
nn.Conv2d(n_ch, 2, kernel_size=1), # (b, 2, h, w)
nn.AdaptiveAvgPool2d((1, 1)), # (b, 2, 1, 1)
nn.Flatten(), # (b, n)
nn.Softplus(),
)
对于中心采用的是sigmoid激活函数,毕竟中心在0.5附近,这样不会存在梯度饱和区间问题
# src/networks/pose.py#L97
def _get_offset_dec(self, n_ch: int) -> nn.Sequential:
"""Return principal point estimation decoder. (b, c, h, w) -> (b, 2)"""
return nn.Sequential(
self.block(n_ch, n_ch, kernel_size=3, stride=1, padding=1),
self.block(n_ch, n_ch, kernel_size=3, stride=1, padding=1),
nn.Conv2d(n_ch, 2, kernel_size=1), # (b, 2, h, w)
nn.AdaptiveAvgPool2d((1, 1)), # (b, 2, 1, 1)
nn.Flatten(), # (b, n)
nn.Sigmoid(),
)
随机图像尺度:
在MiDas算法中已经验证了图像的尺寸会对深度估计造成影响,为了使得网络更加鲁棒和具备更强零样本泛化能力,这里对图像进行剪裁和resize操作。在剪裁的时候涵盖图像高度的
[
50
%
,
100
%
]
[50\%,100\%]
[50%,100%]这个区间,并且长宽比例也会变化,比如1:1、16:9等。
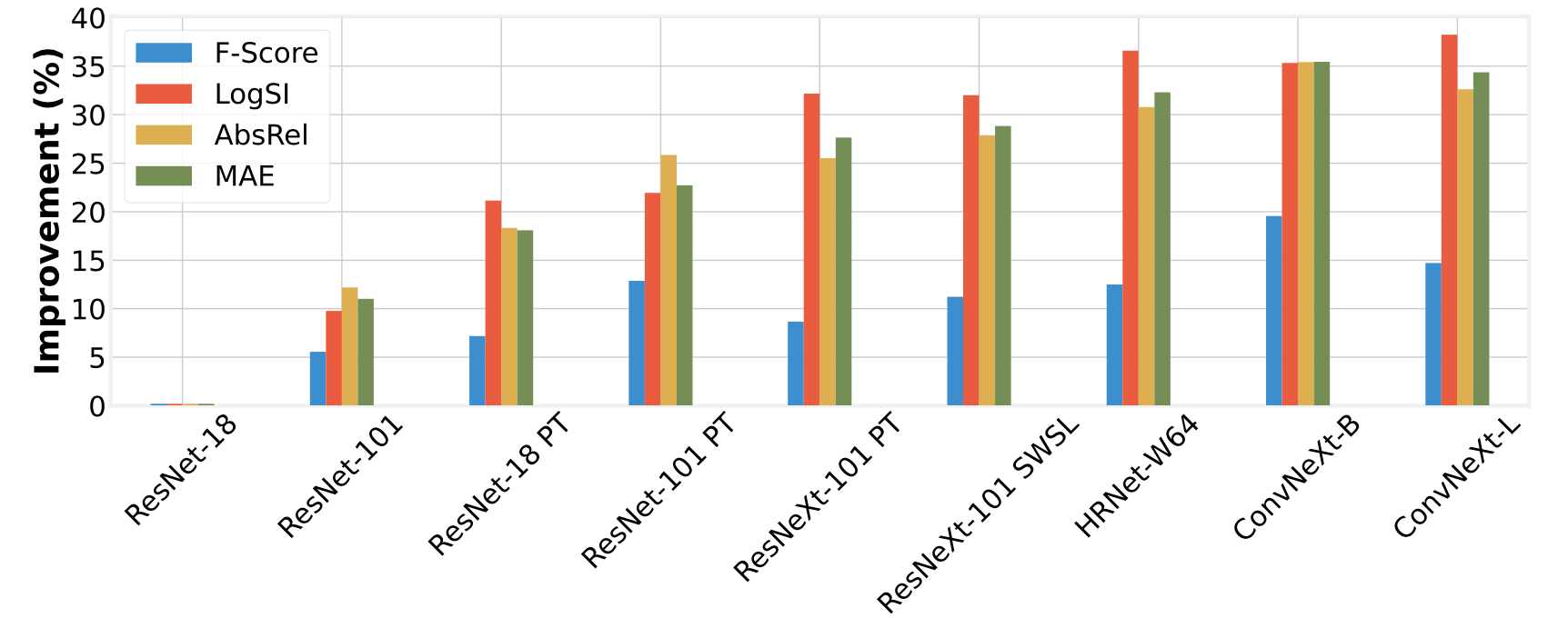
上面的这几个变量对网络性能的消融实验:
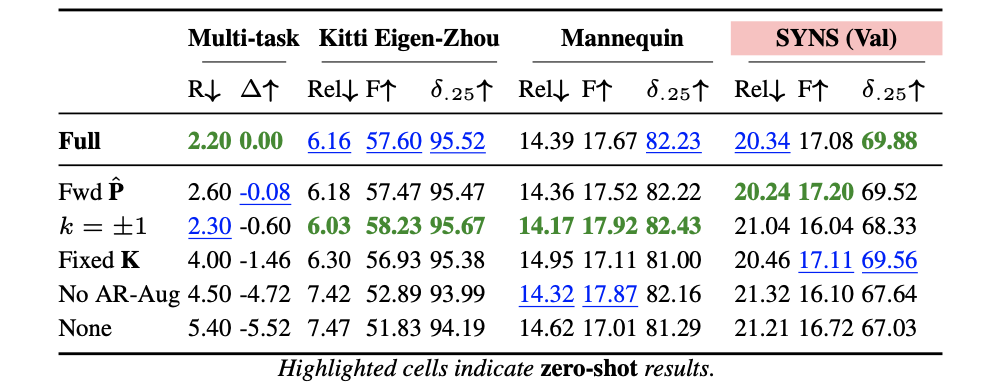
自监督深度估计的性能影响因子:
以下的内容来自于与这篇文章同一个团队的工作,研究的是自监督深度估计算法中backbone、损失函数等对自监督深度估计带来的影响:
paper:Deconstructing Self-Supervised Monocular Reconstruction: The Design Decisions that Matte
backbone对网络性能的影响因素最大:
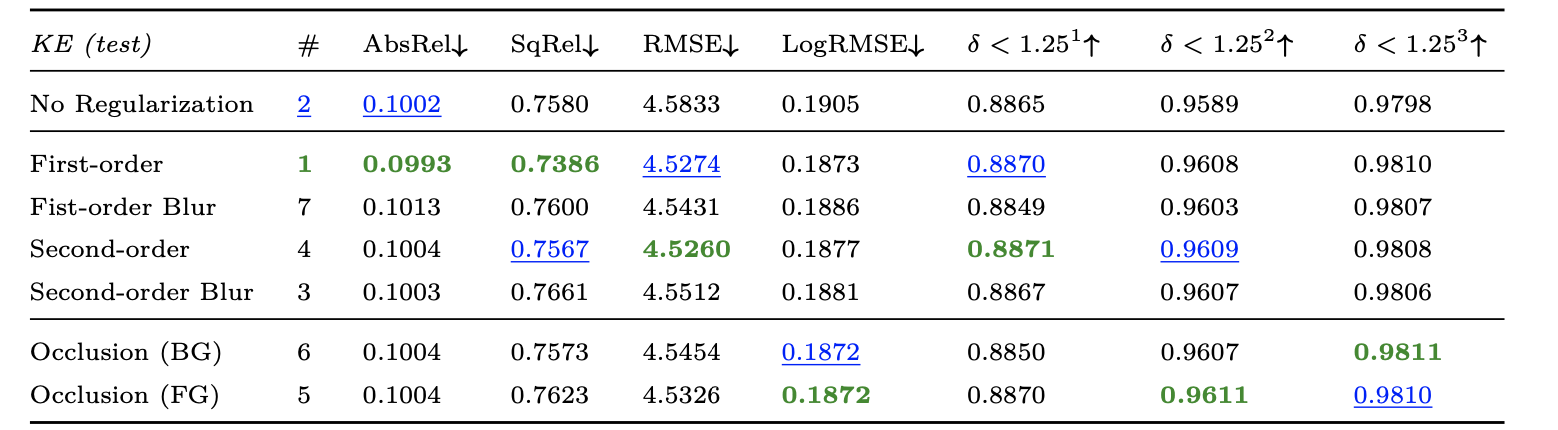
深度估计的平滑对深度性能的波动较小:

![ElementPlusError 解决: [ElForm] model is required for validate to work 的三种方式](https://img-blog.csdnimg.cn/b5616ca9dd2645d48a80860ed282f258.png)