文章目录
- 引言
- 三、割平面法
- 四、0-1 型整数规划
- 4.1 0-1 变量的特性
- 4.1.1 投资问题
- 4.1.2 约束条件满足个数问题
- 写在最后
引言
前文我们介绍了整数规划的一种求解方法——分支定界法,可以求解纯整数和混合整数规划问题。现在我们来学习另一种整数规划求解方法——割平面法。
接着,我们还会涉及到 0-1 整数规划的一些内容,是整数规划的一种特殊情形。
三、割平面法
割平面法是受整数规划几何解释的启发而形成的,根据前文的讨论,整数规划的最优解一定是在线性规划松弛问题的最优解附近。

那么,是否可以增加一些附加的约束,将松弛问题最优解附近不含整数解的可行域的多余部分分割来对最优解进行搜索呢?下面我们通过例子来感受割平面法的工作原理。
用割平面法求解下列整数规划问题。

解: 用单纯形法求解线性规划松弛问题,得到的最优单纯形表如下:
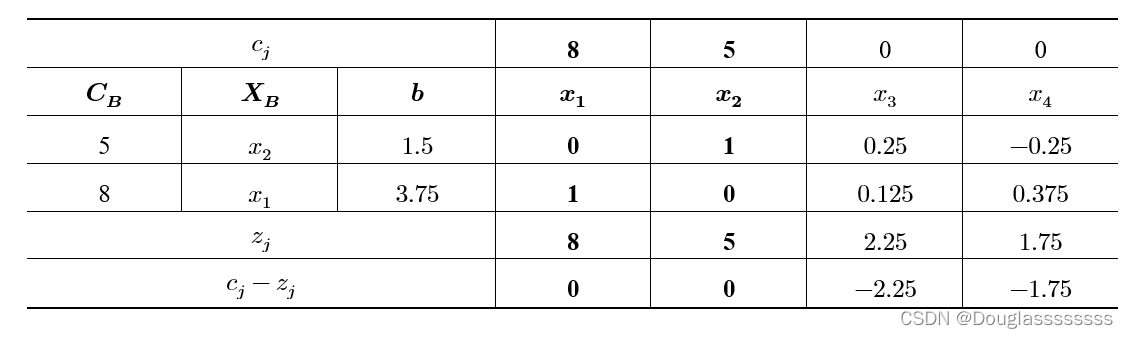
其松弛问题最优解为 ( x 1 = 3.75 , x 2 = 1.5 , z = 37.5 ) (x_1=3.75,x_2=1.5,z=37.5) (x1=3.75,x2=1.5,z=37.5) 。两个基变量均不满足整数要求。割平面通过加入割约束,来割除多余部分。加入割约束的方法为:
从非整数基变量对应的约束条件中任选一个。假定选取第二个,即 x 1 x_1 x1 在最优单纯性表中对应约束。该约束可表示为: x 1 + 0.125 x 3 + 0.375 x 4 = 3.75 x_1+0.125x_3+0.375x_4=3.75 x1+0.125x3+0.375x4=3.75 将上式所有非整数系数写成一个整数和纯正小数之和,即 x 1 + ( 0 + 0.125 ) x 3 + ( 0 + 0.375 x 4 ) = 3 + 0.75 x_1+(0+0.125)x_3+(0+0.375x_4)=3+0.75 x1+(0+0.125)x3+(0+0.375x4)=3+0.75 接着将所有整数项移到等式右边,小数项移到等式左边,可得: x 1 − 3 = 0.75 − 0.125 x 3 − 0.375 x 4 x_1-3=0.75-0.125x_3-0.375x_4 x1−3=0.75−0.125x3−0.375x4 上式,等式左端为整数,则右端也必须为整数。右端 x 3 , x 4 x_3,x_4 x3,x4 均为非负整数,要求等式右端为整数的话,则等式右端要小于等于 0 ,即 0.75 − 0.125 x 3 − 0.375 x 4 ≤ 0 0.75-0.125x_3-0.375x_4 \leq 0 0.75−0.125x3−0.375x4≤0 整理即 − x 3 − 3 x 4 ≤ − 6 -x_3-3x_4 \leq -6 −x3−3x4≤−6 。将其化为等式,添加到之前的最优单纯形表中,利用对偶单纯形法继续求解,得到最优整数解为 ( x 1 = 2 , x 2 = 3 , z = 34 ) (x_1=2,x_2=3,z=34) (x1=2,x2=3,z=34) 。
新加入的割约束方程不会割除任何整数解,即原问题的所有整数解都满足新增加的割约束。
四、0-1 型整数规划
0-1 型整数规划的变量 x i x_i xi 仅取值 0 或 1 。称 x i x_i xi 为 0-1 变量或二进制变量。这一条件可以用以下约束来代替: x i ≤ 1 , x i ≥ 0 , 整数 x_i \leq 1,x_i \geq0,整数 xi≤1,xi≥0,整数
4.1 0-1 变量的特性
面对实际问题中比如逻辑条件或顺序要求等特殊的约束条件,引入 0-1 变量可以非常巧妙地加以表示。下面讨论几个问题,大家就能感受到了。
4.1.1 投资问题
某投资公司可用于投资的资金总额为 b b b ,有若干个项目可供选择投资,假设其中第 j j j 个项目每年可获取利润 c j c_j cj ,所需要的资金是 a j a_j aj ,问如何建立模型来选定最佳组合的投资项目,以取得最佳利润。
这个问题是比较棘手的,但如果引入一个 0-1 变量,建模就变得较为直观和轻松了。因为每一种项目只有两种状态,因此,令
x
j
=
1
x_j=1
xj=1 表示投资了第
j
j
j 个项目,
x
j
=
0
x_j=0
xj=0 表示不投资该项目。可列出如下规划模型:

0-1 变量还可以帮助我们满足现实投资问题中特殊的要求,如下列举了一些例子。
排斥需求—— 某几个项目(假设为第 1,4,5 个项目)中至多只能选一个,约束方程可以表示为 x 1 + x 4 + x 5 ≤ 1. x_1+x_4+x_5 \leq 1. x1+x4+x5≤1.
优先级需求—— 选择了第 2 个项目时,才能考虑选择第 3 个项目,约束可表示为 x 3 ≤ x 2 . x_3 \leq x_2. x3≤x2. 同时选择了第 1,2 个项目时,才能考虑选择第 3 个项目,则约束方程可表示为 2 x 3 ≤ x 1 + x 2 . 2x_3 \leq x_1+x_2. 2x3≤x1+x2.
不可缺需求—— 第 3,4 个项目至少要有一个选择投资,则约束方程可表示为 x 3 + x 4 ≥ 1. x_3+x_4 \geq 1. x3+x4≥1.
4.1.2 约束条件满足个数问题
用下式表示 p p p 个约束条件方程: ∑ j = 1 n a i j x j ≤ b i , i = 1 , 2 , … , p \sum_{j=1}^na_{ij}x_j \leq b_i,i=1,2,\dots,p j=1∑naijxj≤bi,i=1,2,…,p 设 y i y_i yi 为 0-1 变量,如果让第 i i i 个约束条件起作用,则 y i y_i yi 取 1 ,否则取 0 ,即有下式: ∑ j = 1 n a i j x j ≤ b i + ( 1 − y i ) M , i = 1 , 2 , … , p \sum_{j=1}^na_{ij}x_j \leq b_i+(1-y_i)M,i=1,2,\dots,p j=1∑naijxj≤bi+(1−yi)M,i=1,2,…,p 其中, M M M 是很大的整数。此时如何 y i y_i yi 为 0 ,则不等式右端为 b i + M b_i+M bi+M ,显然对任意 x x x 均满足,因此不具有约束力。
若要求必须满足 k k k 个约束条件,可添加条件 ∑ y i = k \sum y_i=k ∑yi=k 。要求至少满足 k k k 个约束条件,可添加条件 ∑ y i ≥ k . \sum y_i \geq k. ∑yi≥k.
写在最后
后文将介绍 0-1 整数规划的解法,是比较重要的内容。