1. 时 域
   时域即时间域，是指以时间作为自变量，振幅作为因变量，在二维坐标图中即 横轴为时间，纵轴为振幅
   下面举出例子：
   频率为$$2Hz$$振幅为$$10V$$
   

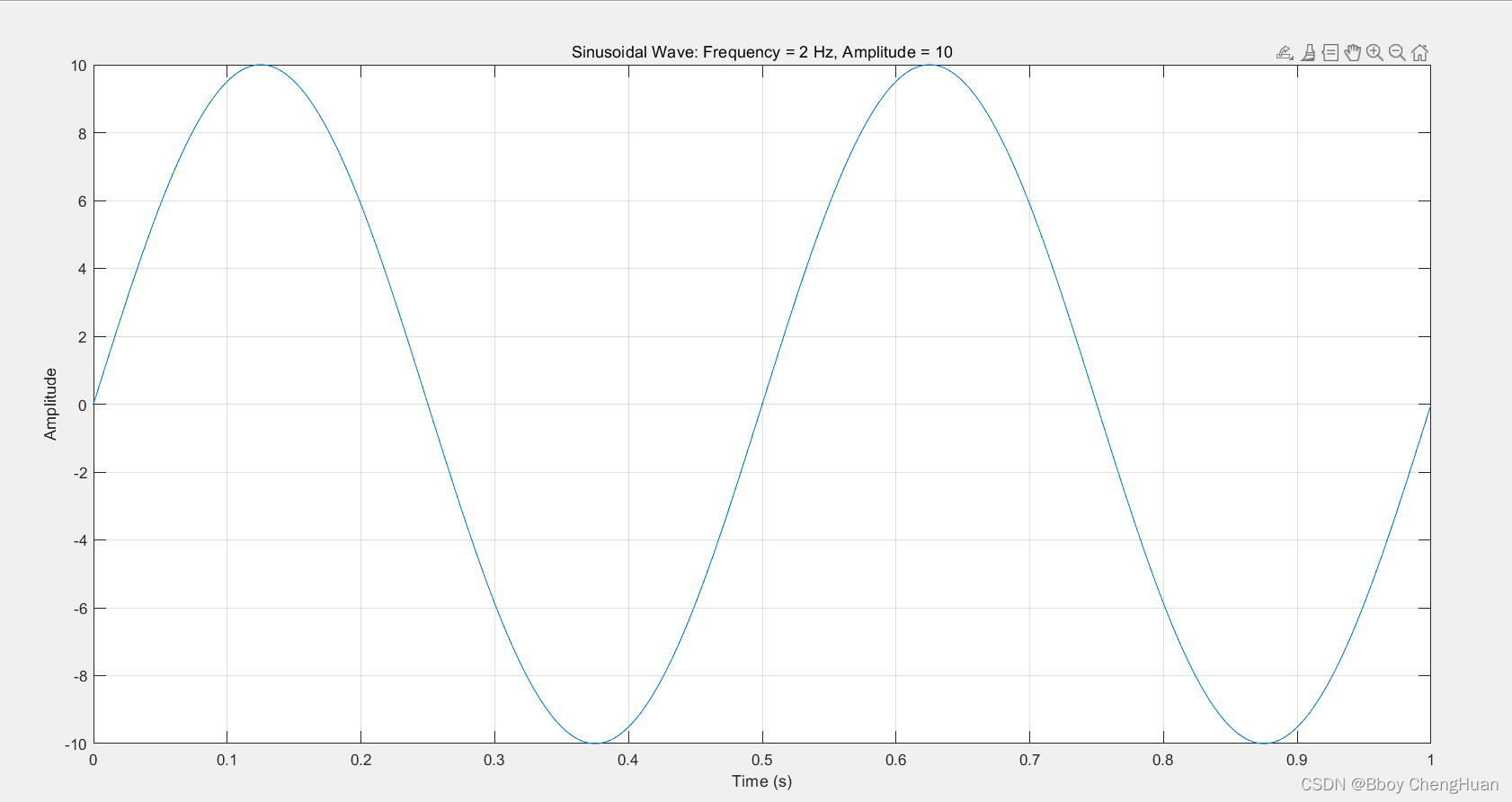
2. 频 域
   同理频域为频率为自变量即横轴 ，对于的因变量可以是幅度或者相位统称为频谱图$$频谱=\{\begin{array}{l}幅度谱\\ 相位谱\end{array}$$
   上图对应的幅度谱应为
   
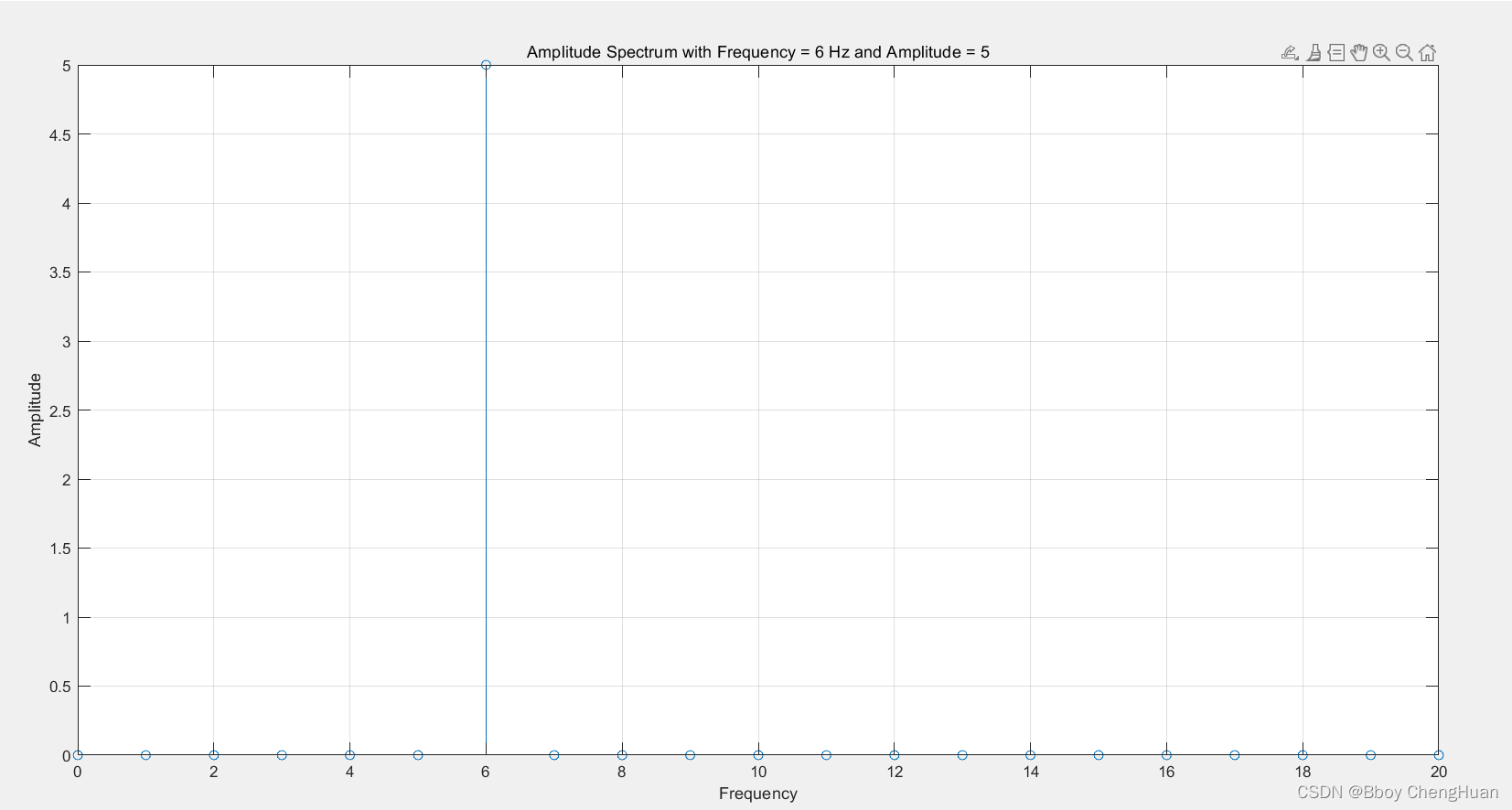
   频谱图：将幅度和相位分量用一定高度的直线表示。其中幅度谱反映信号不同频率分量的大小,频域分为两种形式的分解：
   三角函数形式分解：
   $$f(t)=\frac{A_0}{2}+\sum _{n=0}^{\infty }{A}_{n}cos(n\Omega t+{\phi }_n)$$
   虚指数函数形式分解
   $$f(t)=\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn\Omega t}$$

3. 时域与频域转换
   时域和频域的转换通过傅里叶级数（周期信号）和傅里叶变换（非周期信号），
   
   对于周期信号的的傅里叶变换和傅里叶级数它们之间也是有变换关系。
   另外对于域之间转换是根据需求来转换，还有拉普拉斯变换（S域）、Z变换

参考文章：
时域、频域、空间域的基本概念
傅里叶分析之掐死教程（完整版）更新于2014.06.06

matlab生成正弦函数时域代码块

% 设置参数
frequency = 2; % 频率为6 Hz
amplitude = 10; % 振幅为5

% 生成时间序列
sampling_rate = 1000; % 采样率为1000 Hz
time = 0:1/sampling_rate:1; % 从0秒到1秒，间隔为1/采样率

% 生成正弦波信号
sin_wave = amplitude * sin(2 * pi * frequency * time);

% 绘制时域图
plot(time, sin_wave);
xlabel('Time (s)');
ylabel('Amplitude');
title('Sinusoidal Wave: Frequency = 2 Hz, Amplitude = 10');
grid on;