---

一、堆的概念特性

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆（大根堆）；每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆（小根堆）。

从堆的概念可知，堆是一棵完全二叉树，因此可以使用层序的规则采用顺序的方式来高效存储：

将元素存储到数组中后，可以根据二叉树的性质对树进行还原：

假设i为节点在数组中的下标，则有：

1. 如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2
2. 如果2 * i + 1小于节点个数（左孩子存在条件），则节点i的左孩子下标为2 * i + 1，否则没有左孩子
3. 如果2 * i + 2 小于节点个数（右孩子存在条件），则节点i的右孩子下标为2 * i + 2，否则没有右孩子

二、堆的创建

1、向下调整算法

示例：将集合{75,20,70,30,50,90,80,60,40}调整为小根堆

通过分析，已知集合的 “左右子树均满足小堆的性质” ，我们只需要将根节点向下调整到合适的位置，使集合整体为小堆即可。具体来说，我们可以细化为如下调整方法：

1. 每次调整以待调整结点、它的左右孩子结点构成的子树为单元进行“向下调整”
2. 每个单元以待调整结点为根节点，将左右孩子结点的最小值（小堆）和根节点进行比较，如果根节点<min(左孩子，右孩子)调整结束，否则，待调整根节点和[min(左孩子，右孩子)]交换，交换完成后，继续重复这个步骤直到待调整结点为当前子树单元中的最小值，或待调整结点不在存在孩子结点，调整结束。

按照以上思路，下面是详细的代码实现：

	/**
     * 小根堆->向下调整算法
     * @param parent 待调整结点
     * @param len 数组长度
     */
    private void shiftDown(int[] array,int parent, int len) {
        int child = 2 * parent + 1;//根据完全二叉树性质，找到左孩子
        while (child < len) {
        	//child<len判断孩子合法性
            //满足child<len至少存在左孩子
            if (child + 1 < len && array[child] > array[child + 1]) {
            	//存在右孩子，且右孩子为左右孩子最小值
                child++;
            }
            //此时child一定是左右孩子的最小值的下标
            if (elem[child] < elem[parent]) {
            	//满足条件，就交换
                int tmp = array[parent];
                array[parent] = array[child];
                array[child] = tmp;
				//交换完成后，继续以新的位置向下调整
                parent = child;
                child = 2 * parent + 1;
            } else {
            	//array[parent] < array[child]调整结束
                break;
            }
        }
    }

小结：

1. 在调整以parent为根的二叉树时，必须要满足 parent 的左子树和右子树已经是堆了才可以向下调整。
2. 向下调整算法的最坏情况为从根一直比较到叶子，比较的次数为二叉树的高度，时间复杂度为O(log₂N)。

2、向下调整建堆

在上面的探讨中，我们知道可以使用向下调整算法，将左右子树为堆的完全二叉树序列调整为堆，那么如果给出任意的完全二叉树序列（左右子树不满足堆的特性），我们又该如何调整为堆呢？

思路： 我们已知使用向下调整算法，parent的左右子树必须满足堆的特性，对于任意普通完全二叉树序列，显然不能直接使用向下算法进行调整。不过我们知道一颗完全二叉树是由一颗颗左右子树构成的，虽然一颗普通的完全二叉树不能直接使用向下调整算法，但是倒数第一个非叶子结点构成的子树一定可以使用向下调整算法，所以如果我们可以先将下面的子树调整为堆，在继续对子树的根结点进行调整，这样根节点的左右子树就满足了堆的特性，可以直接使用向下调整算法。就这样一直向上对根结点进行向下调整，直到0下标对应的根节点调整完毕，整颗完全二叉树序列就满足了堆的特性了。

例如以序列{50,70,40,90,20,10,80,30,60}为例，调整后为{10,20,40,30,70,50,80,90,60}

具体实现：

    /**
     * 向下调整建堆
     * @param array
     */
    public void creatHeap(int[] array) {
    	//清晰了思路之后，建堆就非常简单了
    	//只需从最后一个非叶子结点开始，直到找到下标为0的根节点
    	//每遇到一个结点向下调整，调用shiftDown即可
        for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {
            shiftDown(array,parent,array.length);   	 	
        }
    }

3、向下调整建堆的时间复杂度

假设序列为满叉树，假设树高为h，则最坏情况下第K层的2^(k-1)个结要向下移动h-k层。

三、堆的插入

1、向上调整算法实现插入

堆的插入相对来说较为简单，主要分为以下两步：

1. 每次将新节点插入到堆的最后一个节点，因为底层维护的是一个一维数组，空间不够时要扩容。
2. 将新插入的节点 向上调整，直到满足堆的性质。

所以说堆的插入并不难理解，核心就是对向上调整算法的实现：

1. 每次调整以新节点构成的子树为单元，进行“向上调整”。
2. 由于是在堆的基础上进行插入，所以每次调整只需将新节点和根节点进行比较，如果 根节点<新节点（小堆），调整结束，否则，根节点和新节点交换，交换完成后，继续重复这个步骤直到根节点<新节点，或，调整完下标为0的根节点，调整结束。

向上调整代码实现：

    /**
     * 向上调整算法->小根堆
     * @param child 插入下标
     * elem 底层维护的一维数组
     */
    private void shiftUp(int child) {
        int parent = (child-1)/2;根据完全二叉树性质，找双亲
        while (child >0) {
        	//child>0判断孩子节点的合法性
            if (elem[child]<elem[parent]) {
            	//满足条件，交换
                int tmp = elem[parent];
                elem[parent] = elem[child];
                elem[child] = tmp;
				//交换完成后，继续以新的位置向上调整
                child = parent;
                parent = (child-1)/2;
            } else {
            	//elem[child]>elem[parent],调整结束
                break;
            }
        }
    }

堆的插入代码实现：

    /**
     * 插入元素，也可以向上调整建堆
     * @param val
     * @return
     * elem 内部维护数组
     * usedSize 有效长度
     */
    public boolean offerHeap(int val) {
        if (isFull()) {
            //扩容
            elem = Arrays.copyOf(elem,elem.length*2);
        }
        elem[usedSize++]=val;
        shiftUp(usedSize-1);
        return true;
    }

    public boolean isFull() {
        return usedSize==elem.length;
    }

小结：

1. 堆的插入是在堆的基础上进行的插入。
2. 向上调整算法的最坏情况为从叶子节点一直比较到根节点，比较的次数为二叉树的高度，时间复杂度为O(log₂N)。

2、插入创建堆的时间复杂度

最坏情况下，假设堆为一颗满二叉树，的高度为h

三、堆的删除

规定：堆的删除一定删除的是堆顶元素

思路：由于堆的底层维护的是一个一维数组，所以每次删除，我们先将堆顶元素和堆的最后一个元素交换，然后让一维数组的size --，最后将交换后的堆顶元素 向下调整 即可。

1. 判断堆是否为空，空堆不能删除
2. 堆顶元素与堆尾元素交换
3. 内部维护数组的有效数据减少 1
4. 新的堆顶元素向下调整

代码实现：

    /**
     * 删除堆顶元素
     */
    public void pollHeap() {
        //判空
        if (isEmpty()) {
            return;
        }
        //交换
        int tmp = elem[usedSize-1];
        elem[usedSize-1] = elem[0];
        elem[0] = tmp;
        //删除+向下调整
        shiftDown(0,--usedSize);
    }
    public boolean isEmpty() {
        return usedSize == 0;
    }

四、Java集合中的优先级队列

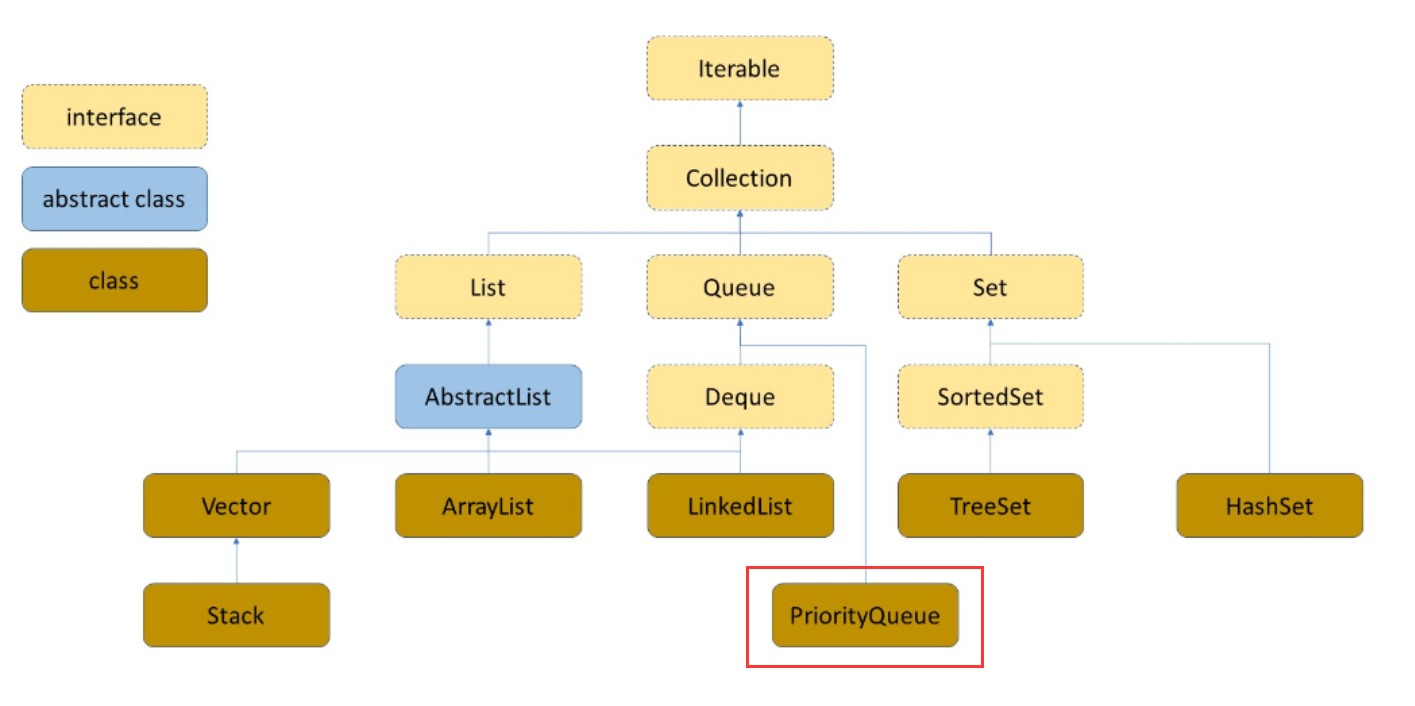
1、PriorityQueue 接口概述及模拟实现

上面我们花那么多时间介绍堆，就是在为Java集合框架中的PriorityQueue做铺垫：

PriorityQueue，即优先级队列。优先级队列可以保证每次取出来的元素都是队列中的最小或最大的元素（Java优先级队列默认每次取出来的为最小元素）。JDK1.8中的PriorityQueue底层使用了堆这种数据结构。

PriorityQueue 注意事项：

1. Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列，PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的。
2. 使用时必须导入PriorityQueue所在的包import java.util.PriorityQueue;
3. PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出 ClassCastException异常
4. 因为 null 无法进行比较和排序，因此不能插入null对象，否则会抛出NullPointerException
5. 没有容量限制，可以插入任意多个元素，其内部可以自动扩容
6. 插入和删除元素的时间复杂度为log₂N
7. PriorityQueue底层使用了堆数据结构，默认情况下是小堆，如果创建大堆，需要在构造方法中传入比较器。

常用的构造方法

构造器	功能介绍
PriorityQueue()	创建一个空的优先级队列，默认容量是11
PriorityQueue(intinitialCapacity)	创建一个初始容量为initialCapacity的优先级队列，注意：initialCapacity不能小于1，否则会抛IllegalArgumentException异常
PriorityQueue(Comparator c)	传入比较器，构造大堆

常用的接口

函数名	功能介绍
boolean offer(E e)	插入元素e，插入成功返回true，如果e对象为空，抛出NullPointerException异常，空间不够时候会进行扩容
E peek()	获取优先级最高的元素，如果优先级队列为空，返回null
E poll()	移除优先级最高的元素并返回，如果优先级队列为空，返回null
int size()	获取有效元素的个数
void clear()	清空
boolean isEmpty()	检测优先级队列是否为空，空返回true

模拟实现PriorityQueue
由于 PriorityQueue 底层使用的是 堆 这种数据结构，所以PriorityQueue中的这些接口函数可以参考上面堆的操作，下面给出完整代码，大家自行理解：

public class PriorityQueue {
    public int[] elem;//数组
    public int usedSize;//有序长度

    public PriorityQueue(){
        elem = new int[11];
    }


	//1.判满
    public boolean isFull() {
        return usedSize==elem.length;
    }
	
	//2.判空
	public boolean isEmpty() {
        return usedSize == 0;
    }
	
	//3.插入元素
    public boolean offerHeap(int val) {
        if (isFull()) {
            //扩容
            elem = Arrays.copyOf(elem,elem.length*2);
        }
        elem[usedSize++]=val;
        shiftUp(usedSize-1);
        return true;
    }
    
    /**
     * 向上调整算法（小根堆）
     * @param child
     * elem 为底层维护的一维数组
     */
    private void shiftUp(int child) {
        int parent = (child-1)/2;
        while (child >0) {
            if (elem[child]<elem[parent]) {
                int tmp = elem[parent];
                elem[parent] = elem[child];
                elem[child] = tmp;

                child = parent;
                parent = (child-1)/2;
            } else {
                break;
            }
        }
    }

    //4.删除堆顶元素
    public void pollHeap() {
        //判空
        if (isEmpty()) {
            return;
        }
        //交换
        int tmp = elem[usedSize-1];
        elem[usedSize-1] = elem[0];
        elem[0] = tmp;
        //删除+向下调整
        shiftDown(0,--usedSize);
    }
	
	 /**
     * 向下调整算法（小根堆）
     * @param parent 待调整结点
     * @param len 数组长度
     */
    private void shiftDown(int parent, int len) {
        //有左孩子
        int child = 2 * parent + 1;//这里是+1！！！
        while (child < len) {
            //有右孩子
            if (child + 1 < len && elem[child] > elem[child + 1]) {
                child++;
            }
            //此时childe一定是左右孩子的最小值的下标
            if (elem[child] < elem[parent]) {
                int tmp = elem[parent];
                elem[parent] = elem[child];
                elem[child] = tmp;

                parent = child;
                child = 2 * parent + 1;
            } else {
                break;
            }
        }
    }

	//5.清空
	public boolean isEmpty() {
        return usedSize == 0;
    }
}

2、如何创建大根堆？

我们已知默认情况下，PriorityQueue 是 小堆，如果创建大堆需要用户提供比较器，关于比较器我在 简介Object类+接口实例（深浅拷贝、对象数组排序）章节中已有过相关介绍，大家可点击连接自行参考，这里就不做过多冗余介绍了。

下面我演示一下创建大根堆常用的 $3$ 中方式（以下这 3 种创建方式，本质上是没有区别的）：

方式1： 直接创建比较类，实现 $Comparator$ 接口，在构造方法中传入，比较类对象。

class Integercmp implements Comparator<Integer>{
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2.compareTo(o1);
    }
}
public class Demo {
	 public static void main1(String[] args) {
        Integercmp cmp = new Integercmp();
        Queue<Integer> maxHeap = new PriorityQueue<>(cmp);
    }
}

方式2： 使用匿名内部类

public class Demo {
	public static void main2(String[] args) {
        Queue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2.compareTo(o1);
            }
        });
    }
}

方式3： 使用 $Lambda$ 表达式

public class Demo {
    public static void main3(String[] args) {
        Queue<Integer> maxHeap = new PriorityQueue<>((o1,o2)->{
            return o2.compareTo(o1);
        });
    }
}