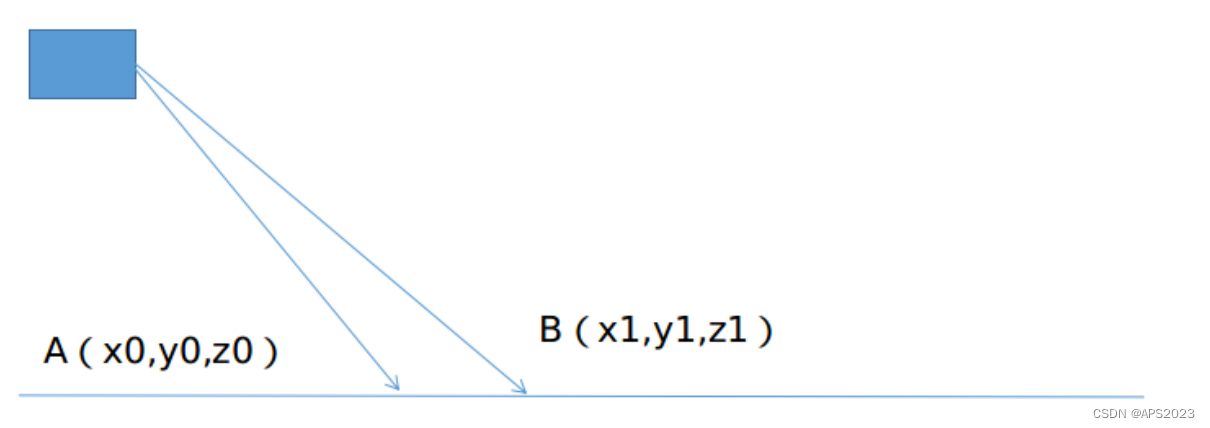1 地面点分离剔除方法
1.1 数学推导
LeGO-LOAM 中前端改进中很重要的一点就是充分利用了地面点,那首先自然是提取
对地面点的提取。
如上图,相邻的两个扫描线束的同一列打在地面上如
点所示,他们的垂直高度差
,水平距离差
,计算垂直高度差和水平高度差的角度
。(这里
为AB到水平面的夹角)理想情况下,
应该接近 0,考虑到一方面激光雷达安装也无法做到绝对水平。另一方面,地面也不是绝对水平。因此,这个角度会略微大于 0,考虑到作者实际在草坪之类的场景下运动,因此这个值被设置成 10 度。
实际上此种地面分离算法有一些简单,我们可以结合激光雷达安装高度等其他先验信息进行优化。
1.2 Lego-LOAM代码实现
版本1:LegoLOAM改版
void ImageProjection::groundRemoval() { // _ground_mat // -1, no valid info to check if ground of not // 0, initial value, after validation, means not ground // 1, ground // 同一列由下到上 _horizontal_scans = 1800 _ground_scan_index=7(地面点的上限)16线设置为7 因为水平地面点不可能在天上面对把 for (size_t j = 0; j < _horizontal_scans; ++j) { for (size_t i = 0; i < _ground_scan_index; ++i) { // 取出同一列相邻点的索引 size_t lowerInd = j + (i)*_horizontal_scans; size_t upperInd = j + (i + 1) * _horizontal_scans; // 非有效点 if (_full_cloud->points[lowerInd].intensity == -1 || _full_cloud->points[upperInd].intensity == -1) { // no info to check, invalid points _ground_mat(i, j) = -1; continue; } float dX = _full_cloud->points[upperInd].x - _full_cloud->points[lowerInd].x; float dY = _full_cloud->points[upperInd].y - _full_cloud->points[lowerInd].y; float dZ = _full_cloud->points[upperInd].z - _full_cloud->points[lowerInd].z; float vertical_angle = std::atan2(dZ , sqrt(dX * dX + dY * dY + dZ * dZ)); // TODO: review this change // 和上文的公式相同 _sensor_mount_angle设置为(_sensor_mount_angle *= DEG_TO_RAD) (DEG_TO_RAD = M_PI / 180.0) if ( (vertical_angle - _sensor_mount_angle) <= 10 * DEG_TO_RAD) { _ground_mat(i, j) = 1; _ground_mat(i + 1, j) = 1; } } } // extract ground cloud (_ground_mat == 1) // mark entry that doesn't need to label (ground and invalid point) for // segmentation note that ground remove is from 0~_N_scan-1, need _range_mat // for mark label matrix for the 16th scan // 遍历特征矩阵 1800 * 16 如果是地面点/无效点的话 设置为-1 不参与线特征面特征的提取 for (size_t i = 0; i < _vertical_scans; ++i) { for (size_t j = 0; j < _horizontal_scans; ++j) { if (_ground_mat(i, j) == 1 || _range_mat(i, j) == FLT_MAX) { _label_mat(i, j) = -1; } } } // RVIZ可视化的操作 for (size_t i = 0; i <= _ground_scan_index; ++i) { for (size_t j = 0; j < _horizontal_scans; ++j) { if (_ground_mat(i, j) == 1) _ground_cloud->push_back(_full_cloud->points[j + i * _horizontal_scans]); } } }版本2:Lego-LOAM原生
void groundRemoval(){ size_t lowerInd, upperInd; float diffX, diffY, diffZ, angle; // groundMat // -1, no valid info to check if ground of not // 0, initial value, after validation, means not ground // 1, ground for (size_t j = 0; j < Horizon_SCAN; ++j){ for (size_t i = 0; i < groundScanInd; ++i){ lowerInd = j + ( i )*Horizon_SCAN; upperInd = j + (i+1)*Horizon_SCAN; if (fullCloud->points[lowerInd].intensity == -1 || fullCloud->points[upperInd].intensity == -1){ // no info to check, invalid points groundMat.at<int8_t>(i,j) = -1; continue; } diffX = fullCloud->points[upperInd].x - fullCloud->points[lowerInd].x; diffY = fullCloud->points[upperInd].y - fullCloud->points[lowerInd].y; diffZ = fullCloud->points[upperInd].z - fullCloud->points[lowerInd].z; angle = atan2(diffZ, sqrt(diffX*diffX + diffY*diffY) ) * 180 / M_PI; if (abs(angle - sensorMountAngle) <= 10){ groundMat.at<int8_t>(i,j) = 1; groundMat.at<int8_t>(i+1,j) = 1; } } } // extract ground cloud (groundMat == 1) // mark entry that doesn't need to label (ground and invalid point) for segmentation // note that ground remove is from 0~N_SCAN-1, need rangeMat for mark label matrix for the 16th scan for (size_t i = 0; i < N_SCAN; ++i){ for (size_t j = 0; j < Horizon_SCAN; ++j){ if (groundMat.at<int8_t>(i,j) == 1 || rangeMat.at<float>(i,j) == FLT_MAX){ labelMat.at<int>(i,j) = -1; } } } if (pubGroundCloud.getNumSubscribers() != 0){ for (size_t i = 0; i <= groundScanInd; ++i){ for (size_t j = 0; j < Horizon_SCAN; ++j){ if (groundMat.at<int8_t>(i,j) == 1) groundCloud->push_back(fullCloud->points[j + i*Horizon_SCAN]); } } } }
2 基于BFS的点云聚类和外点剔除、树干点云提取算法
2.1 数学推导
广度优先遍历(BFS)和深度优先遍历(DFS)同属于两种经典的图遍历的算法。
具体到广度优先遍历算法来说,首先从某个节点出发,一层一层地遍历,下一层必须等到上一层节点全部遍历完成之后才会开始遍历。
比如在上面这个无向图中,如果我们从 A 节点开始遍历,那么首先访问和 A 节点相邻
的节点,这里就是 S、B、D,然后在访问和 S、B、D 相邻的其他节点,这里就是 C。
因此,遍历的顺序是 A->S->B->D->C;如果我们从 S 开始遍历,则顺序就是 S->A->B-
>C->D;可以看到,不同的起始点对应的遍历顺序是不同的。
通常我们使用 BFS 遍历图结构的时候,会借助一个队列 std::queue 来帮助我们实现,
其基本步骤如下:1. 将起始顶点 S 加入队列
2. 访问 S,同时把 S 标记为已访问
3. 循环从队列中取出节
1.如果队列为空,则访问结束
2.否则类似 S,将该节点标记为已访问,同时将其子节点加入队列。
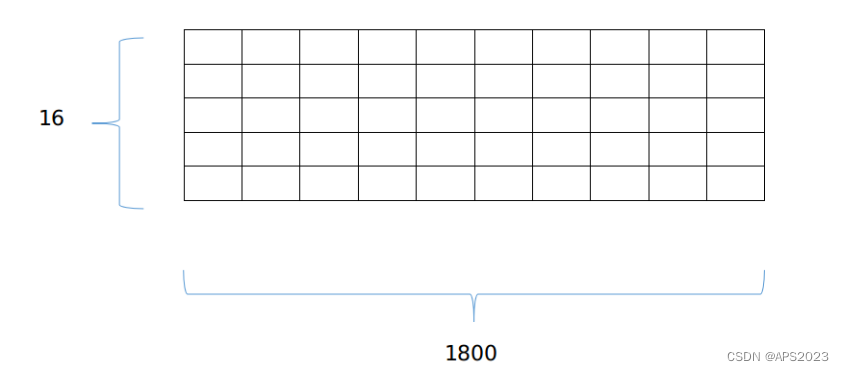
在 LeGO-LOAM 中,BFS 算法用于实现一个简单的点云聚类功能。BFS 算法适用于图数据结构,为了把单帧 lidar 点云运用上 BFS 算法,首先需要将其建模成一个图模型,一个很简单有效的办法就是将其投影到一个平面图上,以velodyne-16 为例,我们将其投影到一个 16×1800 大小的图上(这里 16 是一共有 16跟线束,1800 是因为水平分辨率是 0.2 度,一个扫描周期有 1800 个点)如图:
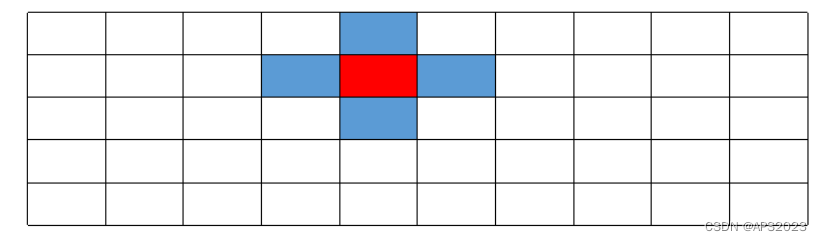
对于任何一个珊格点,其上下左右四个相邻点视为图结构中的邻接节点,这里要注意的是,左右边界的点和边界另一侧也构成邻接,因为水平方向是同一个扫描周期,具有物理意义上的连续性。我们可以以任意一个点开始执行 BFS 搜索,直到遍历完这部分近邻点,聚类点数过少的就认为是 outlier,可以被剔除。
具体实现
1. 遍历每个点,如果该点已经被处理过了就不再处理
2. 如果没有被处理就说明这是一个新的聚类,然后执行 BFS 的步骤
1.将队列里的首元素弹出,然后将该元素近邻塞入队列末尾(这里没有使用std::queue,使用的普通数组,所以就使用双指针来替代)这里的近邻就是上下左右:
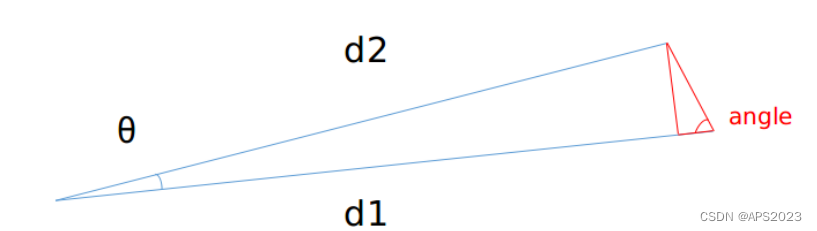
2.分别判断近邻和自身距离是否足够近
angle 越大则认为两点越可能是同一个聚类物体上的点,则打上同样的 label。
3.如此循环
2.2 代码实现
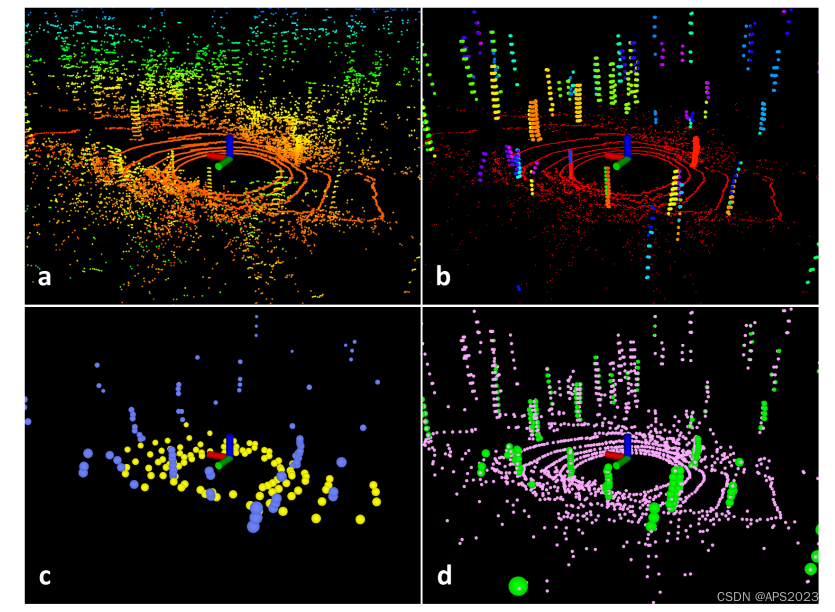
在嘈杂环境中的扫描的特征提取过程。原始点云如图(a)所示。在图(b)中,红色点被标记为地面点。其余的点是分割后保留的点。只保留树干..树叶点都被剔除掉了在图(c)中,蓝色和黄色点表示F e 和 F p 中的边缘和平面特征。在图(d)中,绿色和粉色点分别代表F e 和 F p 中的边缘和平面特征。 广度优先遍历代码:
// 广度优先遍历 void labelComponents(int row, int col){ // use std::queue std::vector std::deque will slow the program down greatly float d1, d2, alpha, angle; int fromIndX, fromIndY, thisIndX, thisIndY; bool lineCountFlag[N_SCAN] = {false}; // 用一个数组保存X坐标,一个数组保存Y坐标 queueIndX[0] = row; queueIndY[0] = col; // 队列里面有多少个点 int queueSize = 1; // 指向前端 int queueStartInd = 0; // 指向即将要加入的位置 int queueEndInd = 1; // 将这个点的(X,Y)坐标赋予给allPushedIndX[0] allPushedIndX[0] = row; allPushedIndY[0] = col; int allPushedIndSize = 1; while(queueSize > 0){ // 将队列的首元素去除,完成广度优先的操作 fromIndX = queueIndX[queueStartInd]; fromIndY = queueIndY[queueStartInd]; // 队列中一共有多少点 --queueSize; // 将指向队列首部的指针向前移动1 ++queueStartInd; // 标记这个点云属于哪一类,当前聚类的ID,当前物体属于同一个ID 在确定当前可以聚类的情况下更新 labelCount,labelCount++ labelMat.at<int>(fromIndX, fromIndY) = labelCount; // 遍历这个结点的邻接顶点,其实就是上下左右四个元素 // std::vector<std::pair<int8_t, int8_t> > neighborIterator; // std::pair<int8_t, int8_t> neighbor; // neighbor.first = -1; neighbor.second = 0; neighborIterator.push_back(neighbor); // neighbor.first = 0; neighbor.second = 1; neighborIterator.push_back(neighbor); // neighbor.first = 0; neighbor.second = -1; neighborIterator.push_back(neighbor); // neighbor.first = 1; neighbor.second = 0; neighborIterator.push_back(neighbor); for (auto iter = neighborIterator.begin(); iter != neighborIterator.end(); ++iter) { // 四个可能的邻接顶点的(X,Y)值 thisIndX = fromIndX + (*iter).first; thisIndY = fromIndY + (*iter).second; // 索引必须在(N_SCAN * HORIZON_SCAN = 16 * 1600中) // 行数不在 0 - 16 间(最上面最下面的点 第1根线或者第8根线的点) if (thisIndX < 0 || thisIndX >= N_SCAN) continue; // 同一根线相距360度且左右相邻 if (thisIndY < 0) thisIndY = Horizon_SCAN - 1; if (thisIndY >= Horizon_SCAN) thisIndY = 0; // 这个顶点是否被访问过 if (labelMat.at<int>(thisIndX, thisIndY) != 0) continue; // 将两个点距离雷达较远的点的距离赋值为d1,较近的点赋值为d2 d1 = std::max(rangeMat.at<float>(fromIndX, fromIndY), rangeMat.at<float>(thisIndX, thisIndY)); d2 = std::min(rangeMat.at<float>(fromIndX, fromIndY), rangeMat.at<float>(thisIndX, thisIndY)); // (0,1) (0,-1) 角分辨率为0.2度--左右糯 if ((*iter).first == 0) alpha = segmentAlphaX; // (1,0) (-1,0) 角分辨率为2度--上下挪动 else alpha = segmentAlphaY; // d2*sin(alpha)为垂线距离 d2*cos(alpha))为垂线的对边 d1 -d2*cos(alpha))为小边 求tan值为angle角度 angle = atan2(d2*sin(alpha), (d1 -d2*cos(alpha))); // 60度(弧度制) 60.0/180.0*M_PI; ----减少这个值会增大精度 if (angle > segmentTheta) { // 丁真 添加到队列中 queueEndInd指向即将要插入的位置中 queueIndX[queueEndInd] = thisIndX; queueIndY[queueEndInd] = thisIndY; ++queueSize; ++queueEndInd; // 标记和前面一种的类型 labelMat.at<int>(thisIndX, thisIndY) = labelCount; // 标志位 : 是否这个点被遍历过设置为true lineCountFlag[thisIndX] = true; // 保存聚类结果 allPushedIndX[allPushedIndSize] = thisIndX; allPushedIndY[allPushedIndSize] = thisIndY; ++allPushedIndSize; } } } // check if this segment is valid bool feasibleSegment = false; // 如果聚类的点大于30,小于30认为是叶子点/噪声点 if (allPushedIndSize >= 30) feasibleSegment = true; // 可能是树杆(垂直于LIDAR扫描方向的) else if (allPushedIndSize >= segmentValidPointNum) { int lineCount = 0; for (size_t i = 0; i < N_SCAN; ++i) if (lineCountFlag[i] == true) ++lineCount; if (lineCount >= segmentValidLineNum) feasibleSegment = true; } // segment is valid, mark these points if (feasibleSegment == true) { // 更新标签值,表示下次是新的一陀东西 ++labelCount; } else { // 聚类无效 for (size_t i = 0; i < allPushedIndSize; ++i) { labelMat.at<int>(allPushedIndX[i], allPushedIndY[i]) = 999999; } } }特征提取前预处理代码:
// 对非地面点聚类 void cloudSegmentation() { // 对所有点进行遍历 N_SCAN=16线 Horizon_SCAN=1800(每根线有1800个点) for (size_t i = 0; i < N_SCAN; ++i) for (size_t j = 0; j < Horizon_SCAN; ++j) if (labelMat.at<int>(i,j) == 0) // 地面点会是-1我们不处理(在上面的代码讲解中已经说过了) // 以这个点为顶点进行广度优先遍历 labelComponents(i, j); int sizeOfSegCloud = 0; // 遍历本帧所有激光点 for (size_t i = 0; i < N_SCAN; ++i) { segMsg.startRingIndex[i] = sizeOfSegCloud-1 + 5; for (size_t j = 0; j < Horizon_SCAN; ++j) { // 要不是有效的距离点 要不是有效的地面点 if (labelMat.at<int>(i,j) > 0 || groundMat.at<int8_t>(i,j) == 1){ // 聚类无效的点 if (labelMat.at<int>(i,j) == 999999){ if (i > groundScanInd && j % 5 == 0){ outlierCloud->push_back(fullCloud->points[j + i*Horizon_SCAN]); continue; } else { continue; } } // 1800列 做一个下采样 点云加密的时候可以用 // groundMat // -1, no valid info to check if ground of not // 0, initial value, after validation, means not ground // 1, ground if (groundMat.at<int8_t>(i,j) == 1) { if (j%5!=0 && j>5 && j<Horizon_SCAN-5) continue; } // 标记地面点,这样在后续提取特征的时候不会被当作角点提取 segMsg.segmentedCloudGroundFlag[sizeOfSegCloud] = (groundMat.at<int8_t>(i,j) == 1); // mark the points' column index for marking occlusion later segMsg.segmentedCloudColInd[sizeOfSegCloud] = j; // 保存距离激光雷达的距离 segMsg.segmentedCloudRange[sizeOfSegCloud] = rangeMat.at<float>(i,j); // 保存点云 segmentedCloud->push_back(fullCloud->points[j + i*Horizon_SCAN]); // 更新下一帧的点的索引 ++sizeOfSegCloud; } } // 同LIO-SAM特征提取的边界 segMsg.endRingIndex[i] = sizeOfSegCloud-1 - 5; } // 发布给RVIZ if (pubSegmentedCloudPure.getNumSubscribers() != 0){ for (size_t i = 0; i < N_SCAN; ++i){ for (size_t j = 0; j < Horizon_SCAN; ++j){ if (labelMat.at<int>(i,j) > 0 && labelMat.at<int>(i,j) != 999999){ segmentedCloudPure->push_back(fullCloud->points[j + i*Horizon_SCAN]); segmentedCloudPure->points.back().intensity = labelMat.at<int>(i,j); } } } } }
3 两步优化的帧间里程计
3.1 理论推导
和原始 LOAM (或者 A-LOAM )一样,通过前后两帧点云来估计两帧之间的运动,从而累加得到前端里程记的输出,和上述方法使用线面约束同时优化六自由度帧间位姿不同,LeGO-LOAM 的前端分成两个步骤,每个步骤估计三自由度的变量:
第一步 利用地面点优化
地面点更符合面特征的性质。因此,地面点的优化问题就使用点到面的约束来构建,同时我们注意到,地面点之间的约束对 x , y 和 yaw 这三个自由度是不能观的。换句话说,当这三个自由度的值发生变化时,点到面的残差不会发生显著变化。所以,地面点之间的优化只会对 pitch , roll 以及 z 进行约束和优化
第二步 利用角点优化
第一步优化完 pitch 、 roll 以及 z 之后,我们仍需对另外三个自由度的变量进行估计,此时,我们选用提取的角点进行优化,由于多线激光雷达提取的角点通常是垂直的边缘特征。因此,这些特征对 x 、 y 以及yaw 有着比较好的能观性,通过角点的优化结合上地面点的结果可以得到六自由度的帧间优化结果。
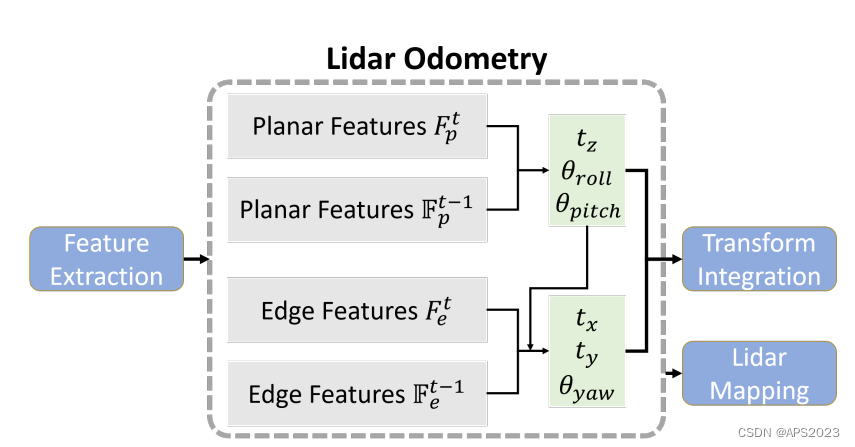
激光里程计模块的两步优化。首先通过匹配从地面点提取的平面特征获得 [t z , θ roll , θ pitch ]。然后,使用从分割点提取的边缘特征来估计 [t x , t y , θ yaw ],同时将 [t z , θ roll , θ pitch ] 作为约束。
3.2 代码实现
void updateTransformation(){ if (laserCloudCornerLastNum < 10 || laserCloudSurfLastNum < 100) return; for (int iterCount1 = 0; iterCount1 < 25; iterCount1++) { laserCloudOri->clear(); coeffSel->clear(); // 平面点优化 findCorrespondingSurfFeatures(iterCount1); if (laserCloudOri->points.size() < 10) continue; if (calculateTransformationSurf(iterCount1) == false) break; } for (int iterCount2 = 0; iterCount2 < 25; iterCount2++) { laserCloudOri->clear(); coeffSel->clear(); // 角点优化 findCorrespondingCornerFeatures(iterCount2); if (laserCloudOri->points.size() < 10) continue; if (calculateTransformationCorner(iterCount2) == false) break; } }每一个部分和LOAM一致,请移步我的多传感器融合的博客。
void findCorrespondingSurfFeatures(int iterCount){ int surfPointsFlatNum = surfPointsFlat->points.size(); for (int i = 0; i < surfPointsFlatNum; i++) { TransformToStart(&surfPointsFlat->points[i], &pointSel); if (iterCount % 5 == 0) { kdtreeSurfLast->nearestKSearch(pointSel, 1, pointSearchInd, pointSearchSqDis); int closestPointInd = -1, minPointInd2 = -1, minPointInd3 = -1; if (pointSearchSqDis[0] < nearestFeatureSearchSqDist) { closestPointInd = pointSearchInd[0]; int closestPointScan = int(laserCloudSurfLast->points[closestPointInd].intensity); float pointSqDis, minPointSqDis2 = nearestFeatureSearchSqDist, minPointSqDis3 = nearestFeatureSearchSqDist; for (int j = closestPointInd + 1; j < surfPointsFlatNum; j++) { if (int(laserCloudSurfLast->points[j].intensity) > closestPointScan + 2.5) { break; } pointSqDis = (laserCloudSurfLast->points[j].x - pointSel.x) * (laserCloudSurfLast->points[j].x - pointSel.x) + (laserCloudSurfLast->points[j].y - pointSel.y) * (laserCloudSurfLast->points[j].y - pointSel.y) + (laserCloudSurfLast->points[j].z - pointSel.z) * (laserCloudSurfLast->points[j].z - pointSel.z); if (int(laserCloudSurfLast->points[j].intensity) <= closestPointScan) { if (pointSqDis < minPointSqDis2) { minPointSqDis2 = pointSqDis; minPointInd2 = j; } } else { if (pointSqDis < minPointSqDis3) { minPointSqDis3 = pointSqDis; minPointInd3 = j; } } } for (int j = closestPointInd - 1; j >= 0; j--) { if (int(laserCloudSurfLast->points[j].intensity) < closestPointScan - 2.5) { break; } pointSqDis = (laserCloudSurfLast->points[j].x - pointSel.x) * (laserCloudSurfLast->points[j].x - pointSel.x) + (laserCloudSurfLast->points[j].y - pointSel.y) * (laserCloudSurfLast->points[j].y - pointSel.y) + (laserCloudSurfLast->points[j].z - pointSel.z) * (laserCloudSurfLast->points[j].z - pointSel.z); if (int(laserCloudSurfLast->points[j].intensity) >= closestPointScan) { if (pointSqDis < minPointSqDis2) { minPointSqDis2 = pointSqDis; minPointInd2 = j; } } else { if (pointSqDis < minPointSqDis3) { minPointSqDis3 = pointSqDis; minPointInd3 = j; } } } } pointSearchSurfInd1[i] = closestPointInd; pointSearchSurfInd2[i] = minPointInd2; pointSearchSurfInd3[i] = minPointInd3; } if (pointSearchSurfInd2[i] >= 0 && pointSearchSurfInd3[i] >= 0) { tripod1 = laserCloudSurfLast->points[pointSearchSurfInd1[i]]; tripod2 = laserCloudSurfLast->points[pointSearchSurfInd2[i]]; tripod3 = laserCloudSurfLast->points[pointSearchSurfInd3[i]]; float pa = (tripod2.y - tripod1.y) * (tripod3.z - tripod1.z) - (tripod3.y - tripod1.y) * (tripod2.z - tripod1.z); float pb = (tripod2.z - tripod1.z) * (tripod3.x - tripod1.x) - (tripod3.z - tripod1.z) * (tripod2.x - tripod1.x); float pc = (tripod2.x - tripod1.x) * (tripod3.y - tripod1.y) - (tripod3.x - tripod1.x) * (tripod2.y - tripod1.y); float pd = -(pa * tripod1.x + pb * tripod1.y + pc * tripod1.z); float ps = sqrt(pa * pa + pb * pb + pc * pc); pa /= ps; pb /= ps; pc /= ps; pd /= ps; float pd2 = pa * pointSel.x + pb * pointSel.y + pc * pointSel.z + pd; float s = 1; if (iterCount >= 5) { s = 1 - 1.8 * fabs(pd2) / sqrt(sqrt(pointSel.x * pointSel.x + pointSel.y * pointSel.y + pointSel.z * pointSel.z)); } if (s > 0.1 && pd2 != 0) { coeff.x = s * pa; coeff.y = s * pb; coeff.z = s * pc; coeff.intensity = s * pd2; laserCloudOri->push_back(surfPointsFlat->points[i]); coeffSel->push_back(coeff); } } } }void findCorrespondingCornerFeatures(int iterCount){ int cornerPointsSharpNum = cornerPointsSharp->points.size(); for (int i = 0; i < cornerPointsSharpNum; i++) { TransformToStart(&cornerPointsSharp->points[i], &pointSel); if (iterCount % 5 == 0) { kdtreeCornerLast->nearestKSearch(pointSel, 1, pointSearchInd, pointSearchSqDis); int closestPointInd = -1, minPointInd2 = -1; if (pointSearchSqDis[0] < nearestFeatureSearchSqDist) { closestPointInd = pointSearchInd[0]; int closestPointScan = int(laserCloudCornerLast->points[closestPointInd].intensity); float pointSqDis, minPointSqDis2 = nearestFeatureSearchSqDist; for (int j = closestPointInd + 1; j < cornerPointsSharpNum; j++) { if (int(laserCloudCornerLast->points[j].intensity) > closestPointScan + 2.5) { break; } pointSqDis = (laserCloudCornerLast->points[j].x - pointSel.x) * (laserCloudCornerLast->points[j].x - pointSel.x) + (laserCloudCornerLast->points[j].y - pointSel.y) * (laserCloudCornerLast->points[j].y - pointSel.y) + (laserCloudCornerLast->points[j].z - pointSel.z) * (laserCloudCornerLast->points[j].z - pointSel.z); if (int(laserCloudCornerLast->points[j].intensity) > closestPointScan) { if (pointSqDis < minPointSqDis2) { minPointSqDis2 = pointSqDis; minPointInd2 = j; } } } for (int j = closestPointInd - 1; j >= 0; j--) { if (int(laserCloudCornerLast->points[j].intensity) < closestPointScan - 2.5) { break; } pointSqDis = (laserCloudCornerLast->points[j].x - pointSel.x) * (laserCloudCornerLast->points[j].x - pointSel.x) + (laserCloudCornerLast->points[j].y - pointSel.y) * (laserCloudCornerLast->points[j].y - pointSel.y) + (laserCloudCornerLast->points[j].z - pointSel.z) * (laserCloudCornerLast->points[j].z - pointSel.z); if (int(laserCloudCornerLast->points[j].intensity) < closestPointScan) { if (pointSqDis < minPointSqDis2) { minPointSqDis2 = pointSqDis; minPointInd2 = j; } } } } pointSearchCornerInd1[i] = closestPointInd; pointSearchCornerInd2[i] = minPointInd2; } if (pointSearchCornerInd2[i] >= 0) { tripod1 = laserCloudCornerLast->points[pointSearchCornerInd1[i]]; tripod2 = laserCloudCornerLast->points[pointSearchCornerInd2[i]]; float x0 = pointSel.x; float y0 = pointSel.y; float z0 = pointSel.z; float x1 = tripod1.x; float y1 = tripod1.y; float z1 = tripod1.z; float x2 = tripod2.x; float y2 = tripod2.y; float z2 = tripod2.z; float m11 = ((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)); float m22 = ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1)); float m33 = ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1)); float a012 = sqrt(m11 * m11 + m22 * m22 + m33 * m33); float l12 = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2) + (z1 - z2)*(z1 - z2)); float la = ((y1 - y2)*m11 + (z1 - z2)*m22) / a012 / l12; float lb = -((x1 - x2)*m11 - (z1 - z2)*m33) / a012 / l12; float lc = -((x1 - x2)*m22 + (y1 - y2)*m33) / a012 / l12; float ld2 = a012 / l12; float s = 1; if (iterCount >= 5) { s = 1 - 1.8 * fabs(ld2); } if (s > 0.1 && ld2 != 0) { coeff.x = s * la; coeff.y = s * lb; coeff.z = s * lc; coeff.intensity = s * ld2; laserCloudOri->push_back(cornerPointsSharp->points[i]); coeffSel->push_back(coeff); } } } }