文章目录
- Ch5. 大数定律与中心极限定理
- (一) 依概率收敛
- (二) 大数定律
- 1.伯努利大数定律
- 2.切比雪夫大数定律
- 3.辛钦大数定律
- (三) 中心极限定理
- 1.列维-林德伯格 中心极限定理 (独立同分布,不指定具体分布,近似服从于标准正态分布)
- 2.德莫弗-拉普拉斯 中心极限定理 (二项分布)
Ch5. 大数定律与中心极限定理
(一) 依概率收敛
设
X
1
,
X
2
,
.
.
.
,
X
n
X_1,X_2,...,X_n
X1,X2,...,Xn是一个随机变量序列,a是一个常数,若对于任意正数
ε
ε
ε,有
lim
n
→
∞
P
{
∣
X
n
−
a
∣
<
ε
}
=
1
或
lim
n
→
∞
P
{
∣
X
n
−
a
∣
≥
ε
}
=
0
\lim_{n→∞}P\{|X_n-a|<ε\}=1 \quad 或 \quad \lim_{n→∞}P\{|X_n-a|≥ε\}=0
n→∞limP{∣Xn−a∣<ε}=1或n→∞limP{∣Xn−a∣≥ε}=0
则称随机变量序列
{
X
n
}
\{X_n\}
{Xn}依概率收敛于a,记为
X
n
→
P
a
X_n\xrightarrow{P}a
XnPa
解题:
①构造
∣
X
n
−
a
∣
<
ε
|X_n-a|<ε
∣Xn−a∣<ε
②求
lim
n
→
∞
P
{
}
=
1
\lim_{n→∞}P\{\}=1
limn→∞P{}=1
(二) 大数定律
1.伯努利大数定律
频率依概率收敛于概率,即 μ n n → P p \dfrac{μ_n}{n}\xrightarrow{P}p nμnPp

2.切比雪夫大数定律
条件:①独立 ②方差存在且一致有上界:
D
(
X
n
)
≤
C
D(X_n)≤C
D(Xn)≤C
结论:
X
‾
→
P
E
X
‾
\overline{X}\xrightarrow{P}E\overline{X}
XPEX

3.辛钦大数定律
条件:①独立 ②同分布 ③期望存在
结论:
X
‾
→
P
E
X
‾
\overline{X}\xrightarrow{P}E\overline{X}
XPEX

推论:
设随机变量序列X1,X2,…,Xn,…相互独立,服从同一分布,且具有k阶矩:
E
(
X
i
k
)
=
μ
k
E(X_i^k) = μ_k
E(Xik)=μk,i=1,2,…,k=1,2,…,则对于任意正数ε,有
lim
n
→
+
∞
P
\lim\limits_{n\rightarrow+\infty}P
n→+∞limP {
∣
1
n
∑
i
=
1
n
X
i
k
−
μ
k
∣
<
ε
|\frac{1}{n}\sum\limits_{i=1}^nX_i^k-μ_k|<ε
∣n1i=1∑nXik−μk∣<ε } = 1
例题1: 切比雪夫大数定律

分析:

答案:D
例题2:

分析:
辛钦大数定律条件:①独立 ②同分布 ③期望存在
答案:C
习题1:14年23(3) 辛钦大数定律

分析:(3)的补集即为辛钦大数定律 (或依概率收敛)
答案:
(3)∵随机变量序列X1,X2,…,Xn相互独立,与总体X服从同一分布,且具有2阶矩
E
(
X
i
2
)
=
E
(
X
2
)
=
θ
E(X_i^2)=E(X^2)=θ
E(Xi2)=E(X2)=θ,i=1,2,…,则对于任意正数ε,有
lim
n
→
+
∞
P
\lim\limits_{n\rightarrow+\infty}P
n→+∞limP {
∣
1
n
∑
i
=
1
n
X
i
2
−
θ
∣
<
ε
|\frac{1}{n}\sum\limits_{i=1}^nX_i^2-θ|<ε
∣n1i=1∑nXi2−θ∣<ε } = 1。
即存在实数a=θ,使得对于任意ε>0,均有
lim
n
→
+
∞
P
\lim\limits_{n\rightarrow+\infty}P
n→+∞limP {
∣
θ
^
−
a
∣
≥
ε
|\hat{θ}-a|≥ε
∣θ^−a∣≥ε } = 0
(三) 中心极限定理

1.列维-林德伯格 中心极限定理 (独立同分布,不指定具体分布,近似服从于标准正态分布)
X1,X2,…,Xn 独立同分布,期望和方差存在,E(Xi)=μ,D(Xi)=σ2>0,则在n充分大时,近似服从标准正态分布Φ(X)
∑
i
=
1
n
X
i
∼
近似
N
(
n
μ
,
n
σ
2
)
∑
i
=
1
n
X
i
−
n
μ
n
σ
2
∼
近似
N
(
0
,
1
)
lim
n
→
∞
P
{
∑
i
=
1
n
X
i
−
n
μ
n
σ
2
≤
x
}
=
Φ
(
x
)
\sum\limits_{i=1}^nX_i\sim^{近似}N(nμ,nσ^2)\\[5mm] \dfrac{\sum\limits_{i=1}^nX_i-nμ}{\sqrt{nσ^2}}\sim^{近似}N(0,1)\\[7mm] \lim\limits_{n→∞}P\{\dfrac{\sum\limits_{i=1}^nX_i-nμ}{\sqrt{nσ^2}}≤x\}=Φ(x)
i=1∑nXi∼近似N(nμ,nσ2)nσ2i=1∑nXi−nμ∼近似N(0,1)n→∞limP{nσ2i=1∑nXi−nμ≤x}=Φ(x)


例题1:20年8.

分析:先求E(X)、D(X),然后对和标准化
E
(
X
)
=
0
×
1
2
+
1
×
1
2
=
1
2
E(X)=0×\dfrac{1}{2}+1×\dfrac{1}{2}=\dfrac{1}{2}
E(X)=0×21+1×21=21
E
(
X
2
)
=
0
2
×
1
2
+
1
2
×
1
2
=
1
2
E(X^2)=0^2×\dfrac{1}{2}+1^2×\dfrac{1}{2}=\dfrac{1}{2}
E(X2)=02×21+12×21=21
D
(
X
)
=
E
(
X
2
)
−
E
2
(
X
)
=
1
2
−
1
4
=
1
4
D(X)=E(X^2)-E^2(X)=\dfrac{1}{2}-\dfrac{1}{4}=\dfrac{1}{4}
D(X)=E(X2)−E2(X)=21−41=41
∴
∑
i
=
1
100
X
i
∼
近似
N
(
50
,
25
)
∴\sum\limits_{i=1}^{100}X_i\sim^{近似}N(50,25)
∴i=1∑100Xi∼近似N(50,25)
∑
i
=
1
n
X
i
−
50
5
∼
近似
N
(
0
,
1
)
\dfrac{\sum\limits_{i=1}^nX_i-50}{5}\sim^{近似}N(0,1)
5i=1∑nXi−50∼近似N(0,1)
P
{
∑
i
=
1
100
X
i
−
50
5
≤
55
−
50
5
=
1
}
=
Φ
(
1
)
P\{\dfrac{\sum\limits_{i=1}^{100}X_i-50}{5}≤\dfrac{55-50}{5}=1\}=Φ(1)
P{5i=1∑100Xi−50≤555−50=1}=Φ(1)
答案:B
2.德莫弗-拉普拉斯 中心极限定理 (二项分布)

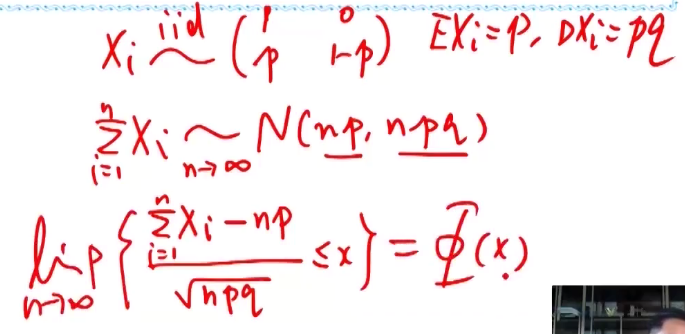


![【C++题解】[2020普及组模拟题]wgy的JX语言](https://img-blog.csdnimg.cn/3d53c79916284bdeb173fd51e64c2617.png)