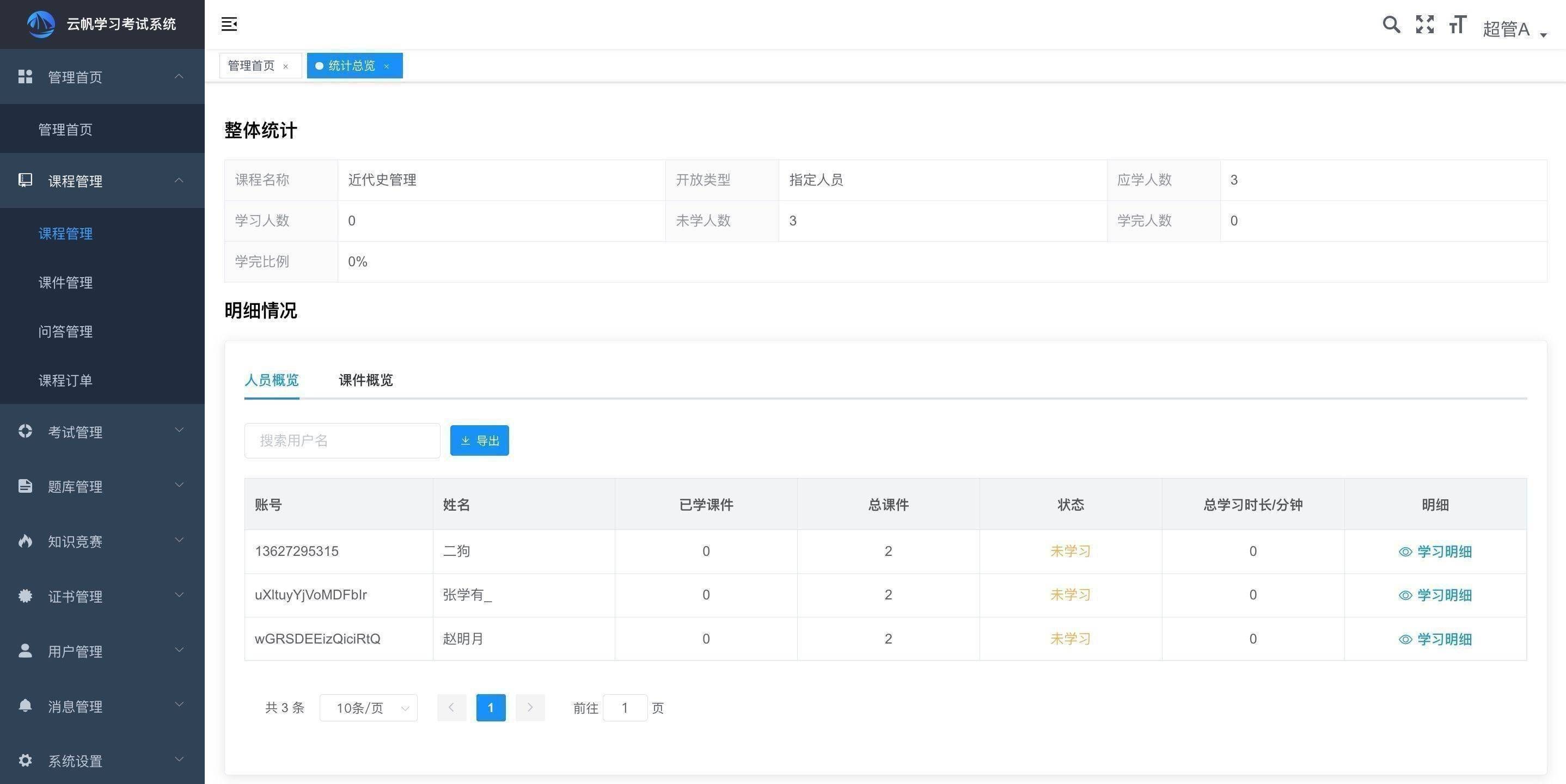
原题链接：Problem - D - Codeforces

题面： 

大概意思就是让你在翻转01串不超过k次的情况下，使得a*（0的最大连续长度）+（1的最大连续长度）最大（1<=a<=n）。输出n个数，第i个数代表a=i时的最大值。

思路：可以发现n<=3000，我们可以用O(n^2)的复杂度来求解。首先我们先假设最长连续0串在左边，最长的连续1串在右边，一开始最朴素的思想就是：

枚举最长0串的左端点l和右端点r，并且使它合法。设区间[l,r]中1的个数为x，也就是说[l,r]变成全0串需要的操作数为x。然后O(n^2)求出区间[r+1,n]我们能得到的最长1串，长度为y（此时我们能进行的最大操作数为k-x）。我们定义mp[i]：0串长度为i时，1串的最长长度为mp[i]。然后我们更新mp[x]为max(mp[r-l+1],y)即可。

因为这是0串在左，1串在右，所以我们还需要将字符串翻转然后再这样处理一次。

最后输出的时候，每次我们只需要遍历mp，a*i+mp[i]取max即可。

当然这样子操作的总复杂度是O(n^4)，我们肯定是不能接受的，那么怎么能让它复杂度降下来呢？我们可以利用dp来预处理，用dp[i][j]来表示[i~n]区间，操作数最大为j时，1串的最大长度。

具体实现见代码注释。

int n,k;
int mp[maxn];
//表示连续0的长度为i的时候，最长连续1的长度最大为mp[i]
string x;
void f() {
	vector<vector<int>>dp(n+2,vector<int>(k+2));
	//dp[i][j]表示[i~n]区间，操作数最大为j时，连续1的最大长度。 
	vector<int>sum(n+2);
	//sum[i]表示[1,i]中字符1的个数 
	string s=" "+x;
	//下标从1开始，防止数组越界 
	for(int i=n; i>=1; i--) {//预处理出i~n的字符串在操作数为k时候变为1的最大连续串长度
		dp[i]=dp[i+1]; 
		//大区间可以由小区间的方案转移过来 ,因为在相同操作数下，[i,n]的最长连续1串 >=[i+1,n]的最长连续1串 
		int cost=0;
		for(int j=i; j<=n; j++) {
			cost+=(s[j]=='0');
			if(cost<=k) dp[i][cost]=max(dp[i][cost],j-i+1);//如果合法，则答案取max 
			else break;//后面的cost都大于k了，直接break 
		}
		for(int j=1; j<=k; j++) dp[i][j]=max(dp[i][j],dp[i][j-1]);
		//大的操作数方案可以由小的操作数方案转移过来，因为你用x次操作能办到的，用x+1次操作也一定能办到 
	}
	mp[0]=max(mp[0],dp[1][k]);//将全是1，没有0的情况特殊处理 
	for(int i=1; i<=n; i++)sum[i]=sum[i-1]+(s[i]=='1');//预处理前缀1的个数 
	for(int i=1; i<=n; i++) {
		for(int j=i; j<=n; j++) {
			if(sum[j]-sum[i-1]>k)continue;//如果操作数大于k了则不合法，continue 
			mp[j-i+1]=max(mp[j-i+1],dp[j+1][k-sum[j]+sum[i-1]]);
			//j-i+1为连续0的长度，k-sum[j]+sum[i-1]为剩下的操作数 
		}
	}
}
void solve() {
	cin>>n>>k>>x;
	for(int i=0; i<=n; i++) mp[i]=-1;//初始化为-1 
	f();//处理0串在左，1串在右的情况 
	reverse(x.begin(),x.end()),f();//等于处理1串在左，0串在右的情况 
	for(int i=1; i<=n; i++) {
		int ans=0;
		for(int j=0; j<=n; j++) {//当0的长度为j时 
			if(mp[j]!=-1)ans=max(ans,i*j+mp[j]);
		}
		cout<<ans<<" ";
	}
	cout<<endl;
}