文章目录

论文详解
- Deformable Convolution
- Deformable RoI Pooling
- Deformable ConvNets
- Understanding Deformable ConvNets
代码详解

论文：《Deformable Convolutional Networks》

论文详解

Deformable Convolution

普通卷积的数学表达
普通的二维卷积包括两个步骤:
1)在输入特征图x上使用regular gird R进行采样;
2)以w加权的采样值的总和。网格R定义接收域的大小和扩张。例如，

$\mathcal{R}=\{(-1,-1),(-1,0), \ldots,(0,1),(1,1)\}$
定义了一个dilation=1, 3x3的卷积。
对于输出特征图 $y$ 上的每个位置 $p_0$ ，
Eq(1)

$\mathbf{y}\left(\mathbf{p}_0\right)=\sum_{\mathbf{p}_n \in \mathcal{R}} \mathbf{w}\left(\mathbf{p}_n\right) \cdot \mathbf{x}\left(\mathbf{p}_0+\mathbf{p}_n\right),$

其中 $p_n$ 穷举了 $\mathcal{R}$ 中的所有位置。

可变形卷积的数学表达
在可变形卷积中，regular grid R用偏移量 $\left\{\Delta \mathbf{p}_n \mid n=1, \ldots, N\right\}$ 进行增广, 其中 $N=|\mathcal{R}|$

上述的式子就变成了：

Eq(2)

$\mathbf{y}\left(\mathbf{p}_0\right)=\sum_{\mathbf{p}_n \in \mathcal{R}} \mathbf{w}\left(\mathbf{p}_n\right) \cdot \mathbf{x}\left(\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n\right)$

现在，采样是在不规则和偏移位置 $p_n+∆p_n$ 上。由于偏移量 $p_n$ 通常为分数阶，因此通过双线性插值实现式(3)为：

Eq(3)

$\mathbf{x}(\mathbf{p})=\sum_{\mathbf{q}} G(\mathbf{q}, \mathbf{p}) \cdot \mathbf{x}(\mathbf{q})$

其中 $p$ 表示任意(分数)位置(对于Eq. (2) $p = p_0 +p_n +∆p_n$ )， $q$ 枚举特征映射x中所有积分空间位置，G(·，·)为双线性插值核。注意G是二维的。它被分成两个一维的核：

Eq(4)

$G(\mathbf{q}, \mathbf{p})=g\left(q_x, p_x\right) \cdot g\left(q_y, p_y\right)$

其中 $g (a, b) = ma x (0, 1 - ∣ a - b ∣)$ 。Eq.(3)的计算速度很快，因为G(q, p)仅在几个q中是非零的。

如图2所示，偏移量是通过在相同的输入特征图上应用卷积层获得的。卷积核与当前卷积层具有相同的空间分辨率和膨胀(图2中也是3 × 3的kernel)。
在这里插入图片描述

个人理解

原始图片的大小为 $b\times c\times h\times w$ ), 记为U(图中的最左边的input feature map)
经过一个普通卷积(上图的conv), 卷积填充为same, 即输出输入大小不变, 对应的输出结果为( $b\times h\times w\times 2N$ ), 记为V 。
输出的结果是指原图片batch中每个像素的偏移量, x方向偏移与y方向的偏移, 因此为2N。（N是指卷积核的大小，如果是3x3的卷积核，则N=9 ）
将U中图片的像素索引值(即坐标)与V(坐标偏移量)相加, 得到偏移后的position (即在原始图片U中的坐标值), 需要将position值限定为图片大小以内, 但position只是一个坐标值, 而且还是float类型的, 我们需要这些float类型的坐标值获取像素。
在这里插入图片描述
如上图所示，只有蓝色的和红色的点存在一个像素值（它们的横纵坐标值均为整数）
假设黄色的点是我们偏移后的position, 它的坐标值设为(a,b), 其中a,b均是浮点数，此时黄色的点的位置是不存在像素值的。
那么怎样才可以得到黄色点对应的像素值呢？我们利用黄色点周围的4个像素点（红色的点）进行双线性插值。
红色点对应的坐标是坐标 $(f l oor (a), f l oor (b)), ((f l oor (a), ce i l (b)), ((ce i l (a), f l oor (b)), ((ce i l (a), ce i l (b))$ 这四对坐标每个坐标都对应U中的一个像素值, 而我们需要得到(a,b)的像素值, 这里采用双线性差值的方式计算, 因为一方面得到的像素准确, 另一方面可以进行反向传播。双线性插值参考：《超分任务中常见的上采样方式》

在这里插入图片描述
DCN的卷积过程和普通卷积一样，如上图所示，假设有个2x2的kernel, 它也是以一个2x2的滑窗的形式（绿色的框）在原始图片上从左到右，从上到下进行滑动。
和普通的卷积的区别在于，当滑动到当前位置时，普通卷积会将卷积核（绿点）和原始像素（红点）对应的值相乘后相加，得到输出的值。
可变形卷积是将卷积核（绿点）和采样点（彩色圆圈）对应的值相乘后相加。其中采样点的像素值就是通过上一步的双线性插值得到的。

Deformable RoI Pooling

所有基于区域建议的目标检测方法都采用RoI池化方法。它将任意大小的输入矩形区域转换为固定大小的特征。它将任意大小的输入矩形区域转换为固定大小的特征。

RoI Pooling

给定输入的特征图 $x$ 和一个大小为 $w \times h$ 和左上角为 $p_0$ 的RoI, RoI池化将RoI分成 $k \times k$ 个 bins ( $k$ 是一个自由参数)，并输出 $k \times k$ 的特征图 $y$ 。对于第 $(i, j)$ 个 bin ( $0 \leq i, j < k$ )，

Eq(5)

$\mathbf{y}(i, j)=\sum_{\mathbf{p} \in \operatorname{bin}(i, j)} \mathbf{x}\left(\mathbf{p}_0+\mathbf{p}\right) / n_{i j}$

其中 $n_{ij}$ 是bin中的pixel的数量。第 $(i, j)$ 个bin span为 $\left\lfloor i \frac{w}{k}\right\rfloor \leq p_x<\left\lceil(i+1) \frac{w}{k}\right\rceil$ , $\left\lfloor j \frac{h}{k}\right\rfloor \leq p_y< \left\lfloor (j+1) \frac{h}{k}\right\rfloor$

与Eq.(2)相似，在可变形RoI池化中，将偏移量 ${∆p_{ij}|0≤i, j < k\}$ 加到空间分块位置上。式(5)得到

Eq(6)

$\mathbf{y}(i, j)=\sum_{\mathbf{p} \in \operatorname{bin}(i, j)} \mathbf{x}\left(\mathbf{p}_0+\mathbf{p}+\Delta \mathbf{p}_{i j}\right) / n_{i j}$

通常， $p_{ij}$ 是分数。式(6)通过式(3)和式(4)的双线性插值实现。

图3演示了如何获取偏移量。首先，RoI池化(Eq.(5))生成池化的特征图。从图中，fc层生成归一化的偏移量 $∆\hat p_{ij}$ ，然后通过与RoI的宽度和高度的元素级乘积转换为公式(6)中的偏移量∆pij，即 $\Delta \mathbf{p}_{i j}=\gamma \cdot \Delta \widehat{\mathbf{p}}_{i j} \circ(w, h)$ 。这里γ是一个预定义的标量，用于调节偏移量的大小。经验值为γ = 0.1。为了使偏移学习不受RoI大小的影响，偏移归一化是必要的。

在这里插入图片描述

个人理解
ROI Pooling 将任意大小的特征图转换成固定大小的特征向量。如下图所示，从左到右分别将ROI划分成了1*1个bins、2*2个bins、3*3个bins。就是说，如果我们需要的特征向量大小是 $k^2$ 个，则把原始的RIO划分成 $k\times k$ 个bin，然后对每个bin中的值求平均，就得到了对应的特征向量的值。
在这里插入图片描述
如下图所示，假设原始图片大小是4x4（下图蓝色的实心点）, 然后我们把原始图片划分成2x2个bins(下图中4个框)。
如果是普通的ROI Pooling，会对每个框中的4个蓝色的实心点对应的像素值求平均。
如果是可变形的ROI Pooling, 会对每个框中的采样点（图中的圆圈）求平均。采样点的像素值和上文中提到的可变形卷积中的一样，也是通过双线性插值得到的。
在这里插入图片描述

Position-Sensitive (PS) RoI Pooling

PS ROI Pooling 是fully convolutional的，不同于RoI Pooling。通过一个conv层，所有的输入特征图首先被转换为每个对象类的 $k^2$ score map (C对象类总共C + 1)，如图4的底部分支所示。不需要区分类别，这样的分数映射被表示为 ${x_{i,j}}$ ，其中 $(i, j)$ 枚举所有的bins。在这些score map上执行池化。第(i, j)个bin的输出值是由对应于该bin的一个得分映射 $x_{i,j}$ 的总和得到的。简而言之，与式(5)中的RoI池化不同的是，将一般的feature map x替换为特定的positive-sensitive score map $x_{i,j}$ 。

在这里插入图片描述

个人理解
我们通过R-FCN论文中的图来理解位置敏感的ROI Pooling (Position-Sensitive RoI Pooling)
如下图，R-FCN会在共享卷积层的最后再接上一层卷积层，而该卷积层输出的结果就是position-sensitive score map
在这里插入图片描述

position-sensitive score map的height和width和共享卷积层的一样，但是它的channels= $k^2(C+1)$ 。那么C表示物体类别种数再加上1个背景类别，每个类别都有 $k^2$ 个score maps。
因为特征图划分成 $k\times k$ 个bins, 把每个类别的第 $i$ 个特征图的第 $i$ 个bin区域按照bin原本的位置组合在一起，构成一个类别的score map。
score map出现高响应值的位置，表示该位置有该类别的概率很大。每个类别的score map在通道维度连接在一起，就构成了 $k\times k \times (C+1)$ 的张量。

对于每个类别，该类别的 $k^2$ 个值都表示该ROI属于该类别的响应值，则把这个 $k^2$ 个值相加，就得到了该类别的Score, 所有类别的score构成了一个 $C + 1$ 的张量，再经过softmax，就可以得到属于各个类别的概率。

Deformable ConvNets

可变形卷积和RoI池化模块的输入和输出与普通版本相同。因此，它们可以很容易地替换现有cnn中的普通版本。在训练中，这些为偏移学习增加的conv层和fc层以零权值初始化。它们的学习率设置为现有层学习率的β倍(β默认为1,fc层在Faster R-CNN中为β = 0.01)。通过式(3)和式(4)中的双线性插值运算进行反向传播训练。得到的cnn称为deformable ConvNets.。

为了将可变形的卷积神经网络与最先进的CNN架构集成在一起，我们注意到这些架构包括两个阶段。首先，深度全卷积网络生成整个输入图像的特征映射。其次，基于任务的浅层网络根据特征映射生成结果。我们将在下面详细说明两个步骤。

Deformable Convolution for Feature Extraction

我们采用了两种最先进的特征提取架构:ResNet-101[20]和InceptionResNet[46]的修改版本。两者都是在ImageNet[7]数据集上预训练的。

最初的Inception-ResNet是为图像识别而设计的。它存在特征不对齐的问题，对于密集的预测任务是有问题的。对其进行了修改，以解决对准问题[18]。修改后的版本被称为“Aligned-Inception-ResNet”。请在本文的arxiv在线版本中找到它的详细信息。

两个模型都由几个卷积块、一个平均池和一个用于ImageNet分类的1000路fc层组成。去掉了平均池和fc层。最后加入一个随机初始化的1 × 1卷积，使信道维数减少到1024。在通常的实践中[3,6]，最后一个卷积块的有效步长从32像素减小到16像素，以提高feature map的分辨率。具体来说，在最后一个区块的开始，步幅从2改变为1(“conv5”的ResNet-101和Aligned-Inception-ResNet)。为了进行补偿，将该块(内核大小为> 1)中所有卷积滤波器的扩展从1更改为2。

可选地，可变形卷积应用于最后几个卷积层(内核大小为> 1)。我们实验了不同数量的这类层，发现3是不同任务的一个很好的权衡，如表1所示。
在这里插入图片描述

Segmentation and Detection Networks

在上述特征提取网络的输出特征映射的基础上，构建任务特定网络。

在下文中，C表示对象类的数量。

DeepLab[4]是一种最先进的语义分割方法。它在特征图上添加1 × 1的卷积层，生成表示逐像素分类分数的(C + 1)图。接下来的softmax输出逐像素概率。

Category-Aware RPN与[42]中的region proposal网络几乎相同，只是用(C + 1)类卷积分类器代替了2类(对象或非对象)卷积分类器

Faster R-CNN[42]是最先进的探测器。在我们的实现中，RPN分支被添加到conv4块的顶部，紧随[42]。在之前的实践中[20,22]，在ResNet-101的conv4和conv5块之间插入了RoI池化层，每个RoI留下10层。该设计具有良好的精度，但每roi计算量较高。相反，我们采用了[34]中的简化设计。最后增加RoI池层。在集合RoI特征的基础上，增加了维度1024的两个fc层，然后是边界框回归和分类分支。虽然这样的简化(从10层conv5块到2 fc层)会略微降低精度，但它仍然是一个足够强的基线，在本工作中不需要关注。

可选地，RoI Pooling 层可以更改为Deformable RoI Pooling。

R-FCN[6]是另一种最先进的探测器。它的每roi计算成本可以忽略不计。我们遵循最初的实现。可选地，它的RoI池层可以更改为可变形的位置敏感RoI池。

Understanding Deformable ConvNets

这项工作是建立在增加空间采样位置的卷积和带有额外的偏移的RoI池化并从目标任务的学习偏移。

图5展示了可变形卷积的叠加效果。展示了3层deformabel convolution的叠加效果，由于每层采样 $3\times 3=9$ 个点，每个绿色的激活点，三层下来对应采样 $9^3=729$ 个点（红色）。从左到右分别是背景、小物体、大物体的采样效果。
在这里插入图片描述
表2提供了这种自适应变形的定量证据。

可变形RoI池化的效果类似，如图7所示。网格结构的规律性在标准RoI池中不再适用。相反，部分偏离RoI bin，移动到附近的对象前景区域。增强了定位能力，特别是对非刚体的定位能力。
在这里插入图片描述

思考

为什么叫做可变形卷积呢

在这里插入图片描述
可变形卷积就是给每个卷积核添加一个方向向量，使得卷积核可以自适应的变成任意的形状，因此也叫做”可变形卷积。

可变形卷积有什么用呢？

同一层的CNN的激活单元的感受野尺度相同，传统的方法的感受野位置受限。

不同的位置对应着不同尺度和形变的物体，卷积层需要能够自动的调整尺度和感受野，更好的提取输入的特征
在这里插入图片描述
最上层是在大小不同的两个物体上的一个激活单元，中间层和底层是为了得到上一层激活单元的采样过程。可以看到可变形卷积在采样时可以更贴近物体的形状和尺寸。

代码详解

class DeformConv2D(nn.Module) 就是定义了二维可变形卷积的类。下面我们分别介绍该类中各个方法。

__init__

功能：初始化

class DeformConv2D(nn.Module):
    def __init__(self, inc, outc, kernel_size=3, padding=1, bias=None):
        super(DeformConv2D, self).__init__()
        self.kernel_size = kernel_size # 卷积核的大小
        self.padding = padding # 填充大小
        self.zero_padding = nn.ZeroPad2d(padding) # 用0去填充
        self.conv_kernel = nn.Conv2d(inc, outc, kernel_size=kernel_size, stride=kernel_size, bias=bias) # 二维卷积

forward

功能：定义前向传播的过程

    def forward(self, x, offset):
    	'''
    	x: 原始输入 [b,c,h,w]
    	offset: 每个像素点的偏移 [b,2*N,h,w]
    	N:kernel中元素的个数 = k*k
    	offset 和 x的宽高相同，表示的是对应位置像素点的偏移 
    	offset 的第二个维度大小是2N, 当N=9时，排列顺序是（x1, y1, x2, y2, ...x18，y18）
    	xi表示一个大小为[h,w]的张量，表示对于原始图像中的每个点，对于kernel中的第i个元素，在x轴方向的偏移量
    	yi表示一个大小为[h,w]的张量，表示对于原始图像中的每个点，对于kernel中的第i个元素，在y轴方向的偏移量
    	'''
        dtype = offset.data.type()
        ks = self.kernel_size
        N = offset.size(1) // 2
        
		'''
        下面这段代码的整体功能：将offset中第二维度的顺序从[x1, y1, x2, y2, ...] 变成[x1, x2, .... y1, y2, ...]
        '''
        offsets_index = Variable(torch.cat([torch.arange(0, 2*N, 2), torch.arange(1, 2*N+1, 2)]), requires_grad=False).type_as(x).long()
        # 当b=1,N=9时，offsets_index=[ 0,  2,  4,  6,  8, 10, 12, 14, 16,  1,  3,  5,  7,  9, 11, 13, 15, 17]  
        # offsets_index的大小为[18]
        offsets_index = offsets_index.unsqueeze(dim=0).unsqueeze(dim=-1).unsqueeze(dim=-1).expand(*offset.size())
        # 然后unsqueeze扩展维度，offsets_index大小为[1,18,1,1]
        # expand后，offsets_index的大小为[1,18,h,w]
        offset = torch.gather(offset, dim=1, index=offsets_index)
        # 根据维度dim按照索引列表index将offset重新排序，得到[x1, x2, .... y1, y2, ...]这样顺序的offset
        # ------------------------------------------------------------------------

        # 对输入x进行padding
        if self.padding:
            x = self.zero_padding(x)

        # p表示求偏置后，每个点的位置
        p = self._get_p(offset, dtype)# (b, 2N, h, w)
        p = p.contiguous().permute(0, 2, 3, 1) # (b,h,w,2N)
        
        q_lt = Variable(p.data, requires_grad=False).floor()  #floor是向下取整
        q_rb = q_lt + 1 #  上取整
        # +1相当于向上取整，这里为什么不用向上取整函数呢？是因为如果正好是整数的话，向上取整跟向下取整就重合了，这是我们不想看到的。

        # q_lt[..., :N]代表x方向坐标，大小[b,h,w,N], clamp将值限制在0~h-1
        # q_lt[..., N:]代表y方向坐标, 大小[b,h,w,N], clamp将值限制在0~w-1
        # cat后，还原成原大小[b,h,w,2N]
        q_lt = torch.cat([torch.clamp(q_lt[..., :N], 0, x.size(2)-1), torch.clamp(q_lt[..., N:], 0, x.size(3)-1)], dim=-1).long() # 将q_lt中的值控制在图像大小范围内 [b,h,w,2N]
        q_rb = torch.cat([torch.clamp(q_rb[..., :N], 0, x.size(2)-1), torch.clamp(q_rb[..., N:], 0, x.size(3)-1)], dim=-1).long() # 将q_rt中的值控制在图像大小范围内 [b,h,w,2N]
        '''
        获取采样后的点周围4个方向的像素点
        q_lt:  left_top 左上
        q_rb:  right_below 右下
        q_lb:  left_below 左下
        q_rt:  right_top 右上
		'''
        # 获得lb
        q_lb = torch.cat([q_lt[..., :N], q_rb[..., N:]], -1) # [b,h,w,2N]
        # 获得rt
        q_rt = torch.cat([q_rb[..., :N], q_lt[..., N:]], -1) # [b,h,w,2N]
        '''
        插值的时候需要考虑一下padding对原始索引的影响 
        p[..., :N]  采样点在x方向(h)的位置   大小[b,h,w,N]
        p[..., :N].lt(self.padding) : p[..., :N]中小于padding 的元素，对应的mask为true
        p[..., :N].gt(x.size(2)-1-self.padding): p[..., :N]中大于h-1-padding 的元素，对应的mask为true 
        
       	p[..., N:]  采样点在y方向(w)的位置   大小[b,h,w,N]
        p[..., N:].lt(self.padding) : p[..., N:]中小于padding 的元素，对应的mask为true
        p[..., N:].gt(x.size(2)-1-self.padding): p[..., N:]中大于w-1-padding 的元素，对应的mask为true 
        cat之后，大小为[b,h,w,2N]
        '''
        mask = torch.cat([p[..., :N].lt(self.padding)+p[..., :N].gt(x.size(2)-1-self.padding),
                          p[..., N:].lt(self.padding)+p[..., N:].gt(x.size(3)-1-self.padding)], dim=-1).type_as(p) # 
        #mask不需要反向传播
        mask = mask.detach()
		#p - (p - torch.floor(p))相当于torch.floor(p)
        floor_p = p - (p - torch.floor(p))
       
        
        '''
        mask为1的区域就是padding的区域
        p*(1-mask) : mask为0的 非padding区域的p被保留
        floor_p*mask: mask为1的  padding区域的floor_p被保留
		'''
        p = p*(1-mask) + floor_p*mask
        p = torch.cat([torch.clamp(p[..., :N], 0, x.size(2)-1), torch.clamp(p[..., N:], 0, x.size(3)-1)], dim=-1)


        # 双线性插值的系数 大小均为 (b, h, w, N)
        g_lt = (1 + (q_lt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_lt[..., N:].type_as(p) - p[..., N:])) 
        # (1+左上角的点x - 原始采样点x)*(1+左上角的点y - 原始采样点y)
        g_rb = (1 - (q_rb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_rb[..., N:].type_as(p) - p[..., N:])) 
        # (1-(右下角的点x - 原始采样点x))*(1-(右下角的点y - 原始采样点y))
        g_lb = (1 + (q_lb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_lb[..., N:].type_as(p) - p[..., N:])) 
        # (1+左下角的点x - 原始采样点x)*(1+左上角的点y - 原始采样点y)
        g_rt = (1 - (q_rt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_rt[..., N:].type_as(p) - p[..., N:])) 
        # (1-(右上角的点x - 原始采样点x))*(1-(右上角的点y - 原始采样点y))

        # (b, c, h, w, N)
        x_q_lt = self._get_x_q(x, q_lt, N) # 左上角的点在原始图片中对应的真实像素值
        x_q_rb = self._get_x_q(x, q_rb, N) # 右下角的点在原始图片中对应的真实像素值
        x_q_lb = self._get_x_q(x, q_lb, N) # 左下角的点在原始图片中对应的真实像素值
        x_q_rt = self._get_x_q(x, q_rt, N) # 右上角的点在原始图片中对应的真实像素值

       
        # 双线性插值算法
        # x_offset : 偏移后的点再双线性插值后的值  大小(b, c, h, w, N)
        x_offset = g_lt.unsqueeze(dim=1) * x_q_lt + \
                   g_rb.unsqueeze(dim=1) * x_q_rb + \
                   g_lb.unsqueeze(dim=1) * x_q_lb + \
                   g_rt.unsqueeze(dim=1) * x_q_rt
		'''
        偏置点含有九个方向的偏置，_reshape_x_offset() 把每个点9个方向的偏置转化成 3×3 的形式，
        于是就可以用 3×3 stride=3 的卷积核进行 Deformable Convolution，
        它等价于使用 1×1 的正常卷积核（包含了这个点9个方向的 context）对原特征直接进行卷积。
        '''
        x_offset = self._reshape_x_offset(x_offset, ks) #(b,c,h*ks,w*ks)
        
        out = self.conv_kernel(x_offset)

        return out

_get_p_n

功能：求每个点的偏置方向

    #功能：求每个点的偏置方向
    def _get_p_n(self, N, dtype):
    	# N=kernel_size*kernel_size
        p_n_x, p_n_y = np.meshgrid(range(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1),
                          range(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1), indexing='ij')
        # (2N, 1)
        p_n = np.concatenate((p_n_x.flatten(), p_n_y.flatten()))
        p_n = np.reshape(p_n, (1, 2*N, 1, 1))
        p_n = Variable(torch.from_numpy(p_n).type(dtype), requires_grad=False)

        return p_n # [1,2*N,1,1]

meshgrid后，p_n_x和p_n_y的值为
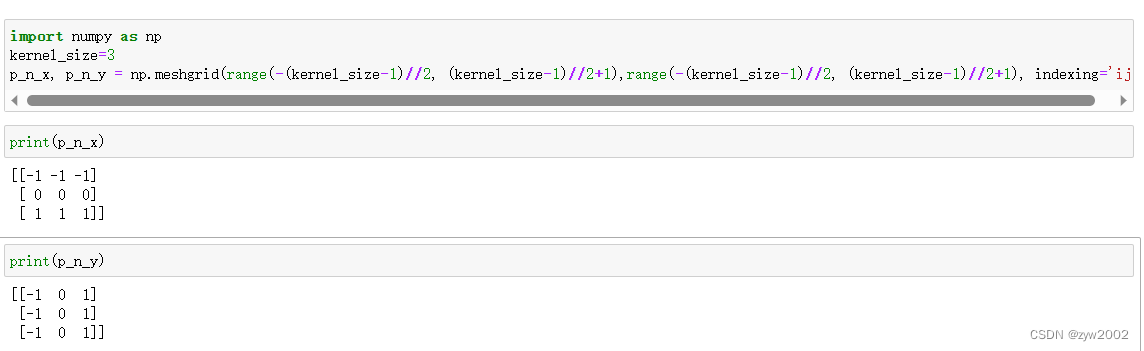
在这里插入图片描述
flatten后，p_n_x和p_n_y的值为

concatenate后，p_n的值为

reshape，p_n的值为:

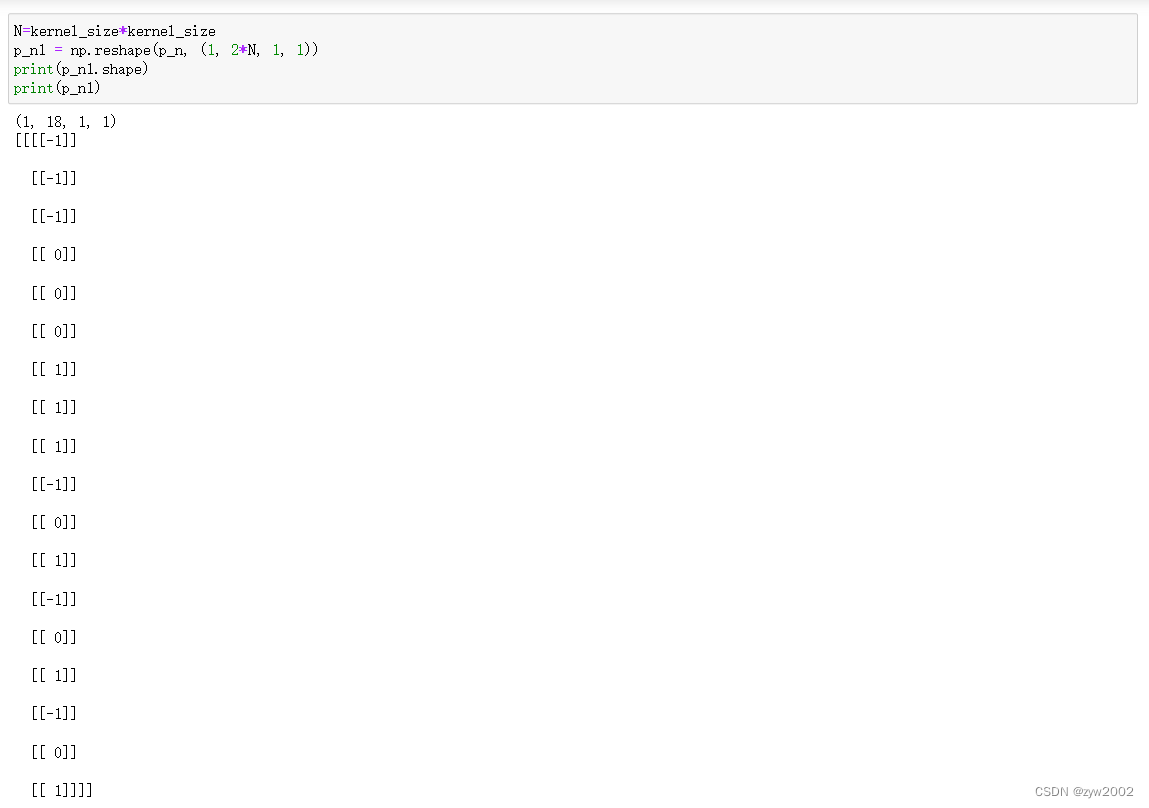
当kernel_size=3时，N=3*3=9 , p_n的大小是[1,18,1,1] (即[1,2*N,1,1])
其中在第二个维度，排列的顺序是·（x1,x2,…,x9,y1,y2,…y9) 。其中xi,yi分别表示kernel中的第i个元素相对于中心点在x方向和y方向的偏移量。

_get_p_0

功能：求每个点的坐标

    @staticmethod
    #功能：求每个点的坐标
    def _get_p_0(h, w, N, dtype):
        p_0_x, p_0_y = np.meshgrid(range(1, h+1), range(1, w+1), indexing='ij')
        p_0_x = p_0_x.flatten().reshape(1, 1, h, w).repeat(N, axis=1) # (1,N,1,1)
        p_0_y = p_0_y.flatten().reshape(1, 1, h, w).repeat(N, axis=1) # (1,N,1,1)
        p_0 = np.concatenate((p_0_x, p_0_y), axis=1)
        p_0 = Variable(torch.from_numpy(p_0).type(dtype), requires_grad=False)

        return p_0 # (1,2*N,1,1)

假设h=3, w=4
meshgrid后，p_0_x, p_0_y的值为
在这里插入图片描述
p_0_x，p_0_y的大小均为[h,w]
flatten后，大小变成[h*w]
reshape后，大小变成[1,1,h,w]
repeat后大小变为[1,9,3,4]
p_0_x的值为：

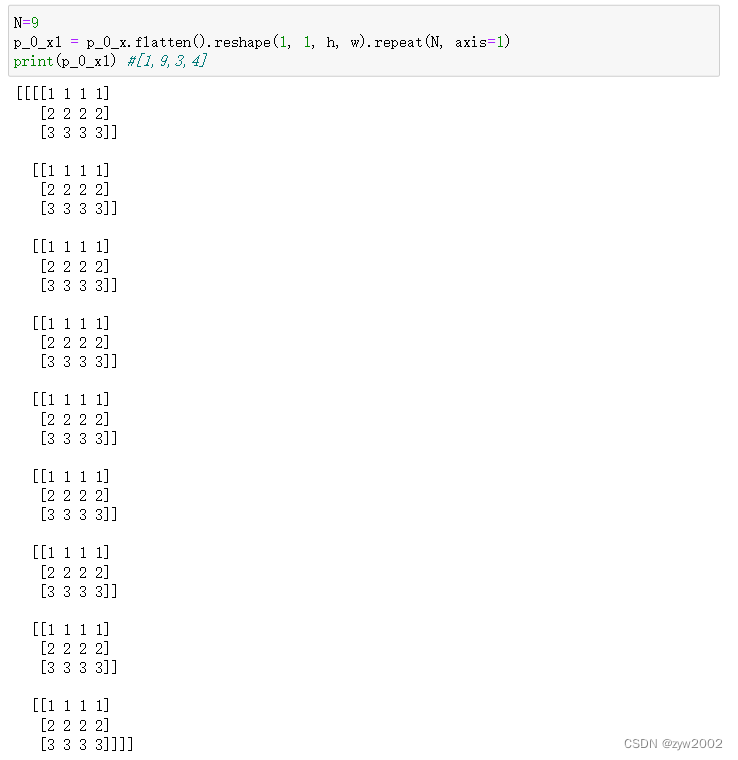
p_0_y的值为：

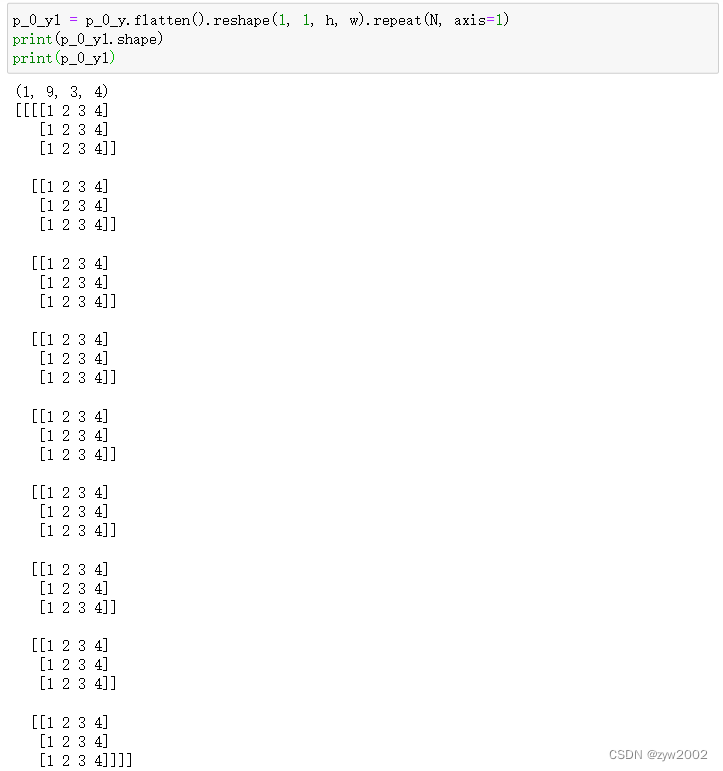
把p_0_x和p_0_y在dim=1上concatenate后，p_0的大小为[1,18,3,4] , 即[b,2*N,h,w]

_get_p
功能：求最后的偏置后的点的位置 = 每个点的坐标(p_0)+偏置方向(p_n)+偏置（offset）

    #求最后的偏置后的点=每个点的坐标+偏置方向+偏置
    def _get_p(self, offset, dtype):
        '''
        offset: 每个像素点的偏移 [b,2*N,h,w]
    	N:kernel中元素的个数 = k*k
    	offset 和 x的宽高相同，表示的是对应位置像素点的偏移 
    	offset 的第二个维度大小是2N, 当N=9时，排列顺序是（x1, y1, x2, y2, ...x18，y18）
    	xi表示一个大小为[h,w]的张量，表示对于原始图像中的每个点，对于kernel中的第i个元素，在x轴方向的偏移量
    	yi表示一个大小为[h,w]的张量，表示对于原始图像中的每个点，对于kernel中的第i个元素，在y轴方向的偏移量
        '''
        N, h, w = offset.size(1)//2, offset.size(2), offset.size(3)
        p_n = self._get_p_n(N, dtype)  # 偏置方向：(1, 2N, 1, 1)
        p_0 = self._get_p_0(h, w, N, dtype) # 每个点的坐标：(1, 2N, h, w)
        p = p_0 + p_n + offset # 最终点的位置
        return p # (1,2N,h,w)

_get_x_q

功能：求采样点周围4个点在原始图像中对应的真实像素值

    #求出p点周围四个点的像素
    def _get_x_q(self, x, q, N):
    	# x:[b,c,h',w']
    	# q:[b,h,w,2N] 
    	# q可能为q_lt,q_rt,q_lb,q_rb
        b, h, w, _ = q.size()
        padded_w = x.size(3) # w'
        c = x.size(1)
        x = x.contiguous().view(b, c, -1) # (b, c, h*w)
        # 将图片压缩到1维，方便后面的按照index索引提取
		
		# q[...,:N]  (b,h,w,N) 原始图像中(h_i,w_j)的点在偏移后，向左上角取整对应的点，在N个区域中，x方向的偏移量
		# q[...,:N]  (b,h,w,N) 原始图像中(h_i,w_j)的点在偏移后，向左上角取整对应的点，在N个区域中，y方向的偏移量
		# index:  (b,h,w,N) 原始图像中(h_i,w_j)的点在偏移后，向左上角取整对应的点，在N个区域中，x*w + y
        index = q[..., :N]*padded_w + q[..., N:]  #    大小(b, h, w, N)
        # 这个目的就是将index索引均匀扩增到图片一样的h*w大小
        
        index = index.contiguous().unsqueeze(dim=1).expand(-1, c, -1, -1, -1).contiguous().view(b, c, -1)
        '''
        unsqueeze后 (b,1,h,w,N)
        expand后 (b,c,h,w,N)
        view后 (b, c, h*w*N) 其中每一个值对应一个index
        '''
        #双线性插值法就是4个点再乘以对应与 p 点的距离。获得偏置点 p 的值，这个 p 点是 9 个方向的偏置所以最后的 x_offset 是 b×c×h×w×9。
        x_offset = x.gather(dim=-1, index=index).contiguous().view(b, c, h, w, N)
        # x :(b,c,h*w)
        # gather后： (b,c,h*w*N)
        # view后：(b,c,h,w,N)
        return x_offset #(b,c,h,w,N) 左上角的点在原始图像中对应的像素值

_reshape_x_offset()

功能：每个点9个方向的偏置转化成 3×3 的形式

    #_reshape_x_offset() 把每个点9个方向的偏置转化成 3×3 的形式
    @staticmethod
    def _reshape_x_offset(x_offset, ks):
    	# x_offset : (b, c, h, w, N)
    	# ks: kernel_size
    	# N=ks*ks
        b, c, h, w, N = x_offset.size()
        '''
        当ks=3,N=9时:
        s=0 [...,0:3]  (b,c,h,w,3)->(b,c,h,w*3)
        s=3 [...,3:6]  (b,c,h,w,3)->(b,c,h,w*3)
        s=6 [...,6:9]  (b,c,h,w,3)->(b,c,h,w*3)
        cat 后 (b,c,h,w*9)
        view 后(b,c,h*3,w*3)
		'''
        x_offset = torch.cat([x_offset[..., s:s+ks].contiguous().view(b, c, h, w*ks) for s in range(0, N, ks)], dim=-1)
        x_offset = x_offset.contiguous().view(b, c, h*ks, w*ks) # (b,c,h*3,w*3)

        return x_offset #(b,c,h*ks,w*ks)