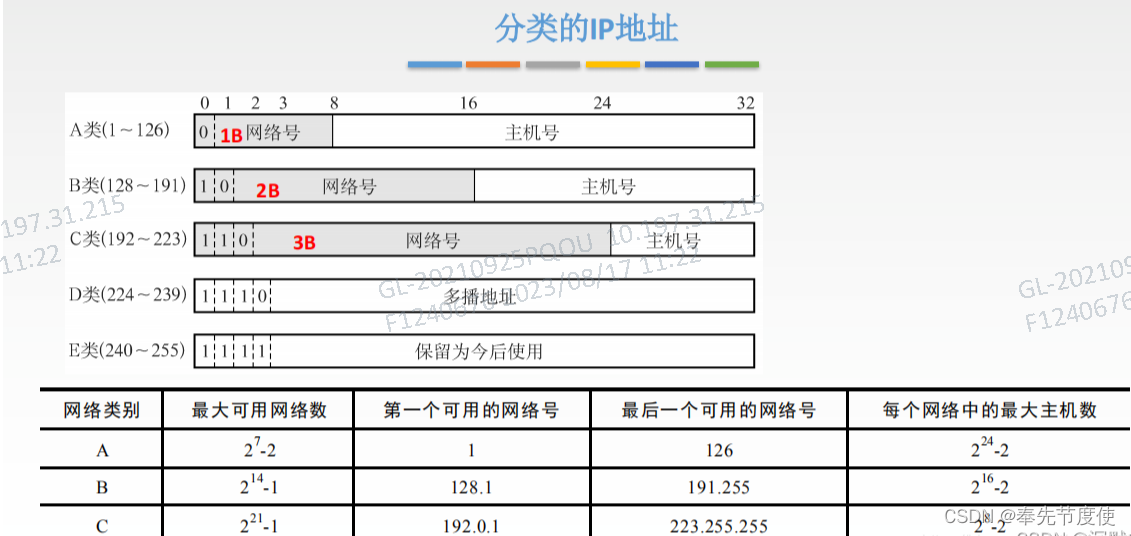
卡尔曼滤波
卡尔曼滤波的设计过程中需要定义两个变量,一个是状态量,另一个是观测量
状态量
- 状态量是跟踪目标。将状态量记作 x n \mathbf{x}_n xn,状态量的协方差矩阵记作 P n \mathbf{P}_n Pn,可以由前一个时刻的状态,估计当前的状态
- 估计过程表示为: x n = F n x n − 1 \mathbf{x}_n=\mathbf{F}_n\mathbf{x}_{n-1} xn=Fnxn−1,其中 x n \mathbf{x}_n xn是一个 N ∗ 1 N*1 N∗1的列向量(小写粗体), F n \mathbf{F}_n Fn是一个 N ∗ N N*N N∗N的矩阵(大写粗体)
- 数学理论:若 x n \mathbf{x}_n xn的协方差矩阵为 P n \mathbf{P}_n Pn,那么 F n x n \mathbf{F}_n\mathbf{x}_n Fnxn的协方差矩阵为 F n P n F n T \mathbf{F}_n\mathbf{P}_n\mathbf{F}_n^T FnPnFnT
- P n = c o v ( x n ) = c o v ( F n x n − 1 ) = F n P n − 1 F n T + Q \mathbf{P}_n=cov(\mathbf{x}_n)=cov(\mathbf{F}_n\mathbf{x}_{n-1})=\mathbf{F}_n\mathbf{P}_{n-1}\mathbf{F}_n^T+\mathbf{Q} Pn=cov(xn)=cov(Fnxn−1)=FnPn−1FnT+Q,其中 Q \mathbf{Q} Q是为了增加协方差矩阵的不确定性
观测量
- 由观测量可以预测状态量。将观测量记作 z n \mathbf{z}_n zn,观测量的协方差矩阵记作 R n \mathbf{R}_n Rn,观测量与状态量之间存在映射关系
- 映射关系表示为: z n = H n x n \mathbf{z}_n=\mathbf{H}_n\mathbf{x}_n zn=Hnxn, R n = H n P n H n T \mathbf{R}_n=\mathbf{H}_n\mathbf{P}_n\mathbf{H}_n^T Rn=HnPnHnT,其中 z n \mathbf{z}_n zn是一个 M ∗ 1 M*1 M∗1的列向量, R n \mathbf{R}_n Rn是一个 M ∗ M M*M M∗M的矩阵, H n \mathbf{H}_n Hn是一个 M ∗ N M*N M∗N的矩阵
- 根据前一个时刻的状态可以估计当前的状态,根据观测量可以映射出当前的状态,但是这两种方法可能都不够准确,因此需要对它们俩的估计结果取一个交集
- 根据两个量的均值和协方差矩阵,得到状态量和观测量的分布,然后计算联合分布,将其作为新的状态量
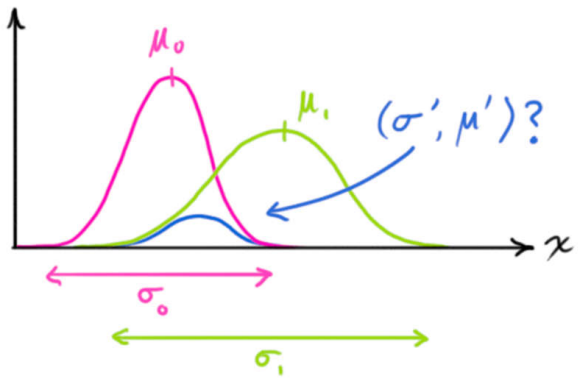
联合分布的更新过程
- 卡尔曼增益
K n = P n H n T ( H n P n H n T + R n ) − 1 \mathbf{K}_n=\mathbf{P}_n\mathbf{H}_n^T(\mathbf{H}_n\mathbf{P}_n\mathbf{H}_n^T+\mathbf{R}_n)^{-1} Kn=PnHnT(HnPnHnT+Rn)−1 - 估计过程
x n + 1 = x n + K n ( z n − H n x n ) \mathbf{x}_{n+1}=\mathbf{x}_{n}+\mathbf{K}_n(\mathbf{z}_n-\mathbf{H}_n\mathbf{x}_n) xn+1=xn+Kn(zn−Hnxn) - 协方差矩阵
P n + 1 = P n − K n H n P n \mathbf{P}_{n+1}=\mathbf{P}_{n}-\mathbf{K}_n\mathbf{H}_n\mathbf{P}_n Pn+1=Pn−KnHnPn
具体到AEC任务
- 卡尔曼滤波预测公式
x n = F n x n − 1 P n = F n P n − 1 F n T + Q \begin{aligned} \mathbf{x}_n&=\mathbf{F}_n\mathbf{x}_{n-1} \\ \mathbf{P}_n&=\mathbf{F}_n\mathbf{P}_{n-1}\mathbf{F}_n^T+\mathbf{Q} \end{aligned} xnPn=Fnxn−1=FnPn−1FnT+Q - 卡尔曼滤波更新公式
K n = P n H n T ( H n P n H n T + R n ) − 1 x n + 1 = x n + K n ( z n − H n x n ) P n + 1 = P n − K n H n P n \begin{aligned} \mathbf{K}_n&=\mathbf{P}_n\mathbf{H}_n^T(\mathbf{H}_n\mathbf{P}_n\mathbf{H}_n^T+\mathbf{R}_n)^{-1} \\ \mathbf{x}_{n+1}&=\mathbf{x}_{n}+\mathbf{K}_n(\mathbf{z}_n-\mathbf{H}_n\mathbf{x}_n) \\ \mathbf{P}_{n+1}&=\mathbf{P}_{n}-\mathbf{K}_n\mathbf{H}_n\mathbf{P}_n \end{aligned} Knxn+1Pn+1=PnHnT(HnPnHnT+Rn)−1=xn+Kn(zn−Hnxn)=Pn−KnHnPn - AEC的预测目标是回声路径 w n \mathbf{w}_n wn,假设回声路径是稳定的,可由N阶线性滤波器模拟,那么 w n = w n − 1 \mathbf{w}_n=\mathbf{w}_{n-1} wn=wn−1, w n \mathbf{w}_n wn是一个 N ∗ 1 N*1 N∗1的列向量,取 x n = w n \mathbf{x}_n=\mathbf{w}_{n} xn=wn,从而 F n = I \mathbf{F}_{n}=\mathbf{I} Fn=I, P n = P n − 1 + Q \mathbf{P}_{n}=\mathbf{P}_{n-1}+\mathbf{Q} Pn=Pn−1+Q
- AEC的滤波输出 e ( n ) = d ( n ) − w n T x n e(n)=d(n)-\mathbf{w}_n^T\mathbf{x}_n e(n)=d(n)−wnTxn,其中 d ( n ) d(n) d(n)是麦克风当前接收信号, x n \mathbf{x}_n xn是参考信号,同样为 N ∗ 1 N*1 N∗1的列向量
- AEC的观测量是麦克风当前接收信号 d ( n ) d(n) d(n), d ( n ) = x n T w n + e ( n ) d(n)=\mathbf{x}_n^T\mathbf{w}_n+e(n) d(n)=xnTwn+e(n),取 z n = d ( n ) \mathbf{z}_n=d(n) zn=d(n),从而 H n = x n T \mathbf{H}_n=\mathbf{x}_{n}^T Hn=xnT(将 e ( n ) e(n) e(n)的期望视作0, z n = H n x n \mathbf{z}_n=\mathbf{H}_n\mathbf{x}_n zn=Hnxn), R n = e ( n ) 2 + δ \mathbf{R}_n=e(n)^2+\delta Rn=e(n)2+δ,其中 δ \delta δ是小常数
- 注意:因为 z n = d ( n ) \mathbf{z}_n=d(n) zn=d(n),所以此时的 z n \mathbf{z}_n zn是一个常数,从而 R n \mathbf{R}_n Rn也是一个常数, H n \mathbf{H}_n Hn是一个 1 ∗ N 1*N 1∗N的行向量
- 代入更新公式
K n = P n x n ( x n T P n x n + R n ) − 1 w n + 1 = w n + K n ( d ( n ) − x n T w n ) = w n + K n e ( n ) P n + 1 = P n − K n x n T P n \begin{aligned} \mathbf{K}_n&=\mathbf{P}_n\mathbf{x}_n(\mathbf{x}_n^T\mathbf{P}_n\mathbf{x}_n+\mathbf{R}_n)^{-1} \\ \mathbf{w}_{n+1}&=\mathbf{w}_{n}+\mathbf{K}_n(d(n)-\mathbf{x}_n^T\mathbf{w}_n)=\mathbf{w}_{n}+\mathbf{K}_{n}e(n) \\ \mathbf{P}_{n+1}&=\mathbf{P}_{n}-\mathbf{K}_n\mathbf{x}_n^T\mathbf{P}_n \end{aligned} Knwn+1Pn+1=Pnxn(xnTPnxn+Rn)−1=wn+Kn(d(n)−xnTwn)=wn+Kne(n)=Pn−KnxnTPn - 综合
P n = P n − 1 + Q e ( n ) = d ( n ) − w n T x n R n = e ( n ) 2 + δ K n = P n x n ( x n T P n x n + R n ) − 1 w n + 1 = w n + K n e ( n ) P n + 1 = P n − K n x n T P n \begin{aligned} \mathbf{P}_{n}&=\mathbf{P}_{n-1}+\mathbf{Q} \\ e(n)&=d(n)-\mathbf{w}_{n}^T\mathbf{x}_{n} \\ \mathbf{R}_n&=e(n)^2+\delta \\ \mathbf{K}_n&=\mathbf{P}_n\mathbf{x}_n(\mathbf{x}_n^T\mathbf{P}_n\mathbf{x}_n+\mathbf{R}_n)^{-1} \\ \mathbf{w}_{n+1}&=\mathbf{w}_{n}+\mathbf{K}_{n}e(n) \\ \mathbf{P}_{n+1}&=\mathbf{P}_{n}-\mathbf{K}_n\mathbf{x}_n^T\mathbf{P}_n \end{aligned} Pne(n)RnKnwn+1Pn+1=Pn−1+Q=d(n)−wnTxn=e(n)2+δ=Pnxn(xnTPnxn+Rn)−1=wn+Kne(n)=Pn−KnxnTPn