解答费米问题有两个重要的思想:
第一个是“逻辑树法”:
用逻辑拆解把一个大的问题拆分为几个小问题,大问题是未知的,而拆解后的小问题是可以通过经验和逻辑推算得出的。最后再把得到解答的小问题反推到大问题上,用已知推导未知,那么未知的问题就能得到解答。
第二个是“平衡率”思想:
在拆解后的问题里面,有一些问题估高了,一些问题估低了,那么综合下来估算的错误就会被抵消。而且做的假设越多,被抵消的概率就越大。
举个经典的例子:
芝加哥有多少个钢琴调音师。
首先对问题进行拆解:
芝加哥有多少个钢琴调音师=芝加哥所有调音师的全年总时长/每名调音师的全年工作时长
=(芝加哥钢琴数*平均每架钢琴调音时长*每年平均每架钢琴要调几次音)/每名调音师全年的工作时长
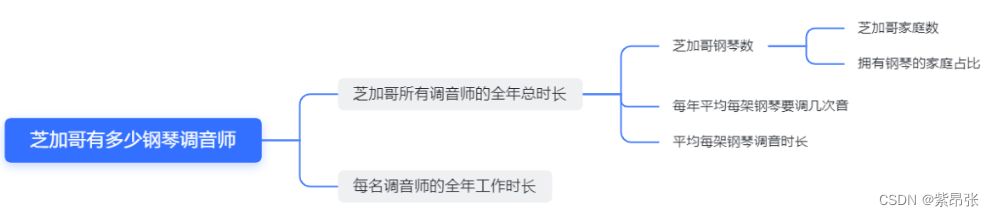
用“平衡率”思想估算:
到了这一步问题就算拆解完了,比如调音几次、调音时长等问题 已经不能继续拆解了。接下来就下一个步骤:问题估算:
| 问题 | 估算思路 | 估算过程 | 结果 |
| 芝加哥钢琴数 | 芝加哥居民300w人,每个家庭4人,共300/4=75w家庭; 拥有钢琴的家庭比例,不多于1/2,不少于1/10,估算为1/3,则钢琴数75w*1/3=25w。 | 芝加哥所有调音师的全年总时长=8.3w*3h=25w h | 25w/3456≈72名 |
| 每年平均每架钢琴要调几次音 | 专业的演奏者钢琴每年都需要调音,但不是所有家庭都需要调,需要调音的家庭占比不超1/2,不少于1/10,估算为1/3,则每年需要调音的钢琴数25w*1/3=8.3w。 | ||
| 平均每架钢琴调音时长 | 每架钢琴调音时长,不超过10h,也不会低于1h,估算为3h。 | ||
| 每名调音师的工作时长 | 调音师工作天数,每个月不超26天,不低于22天,估算为24天,24d*12=288天。 每天的工作时长,调音不多于5架,不低于1架,估算为3架钢琴,加上路程时长往返1h,3*3+3=12h | 288*12=3456 |
结果:25w/3456≈72名
后续:经过费米和学生们事后进行电话号码验证,大概芝加哥市有80位调音师,除去一些号码重复的,其结果竟然跟费米估算的相差无几!