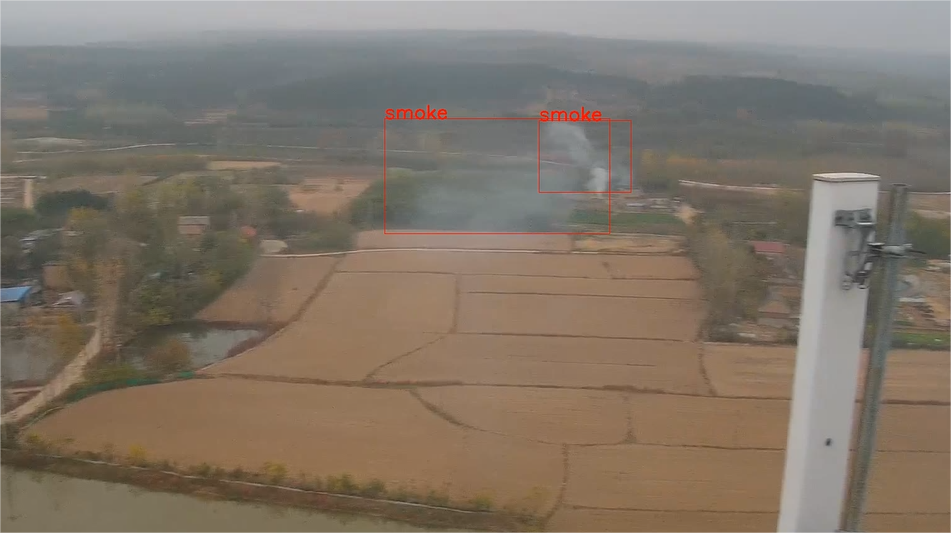
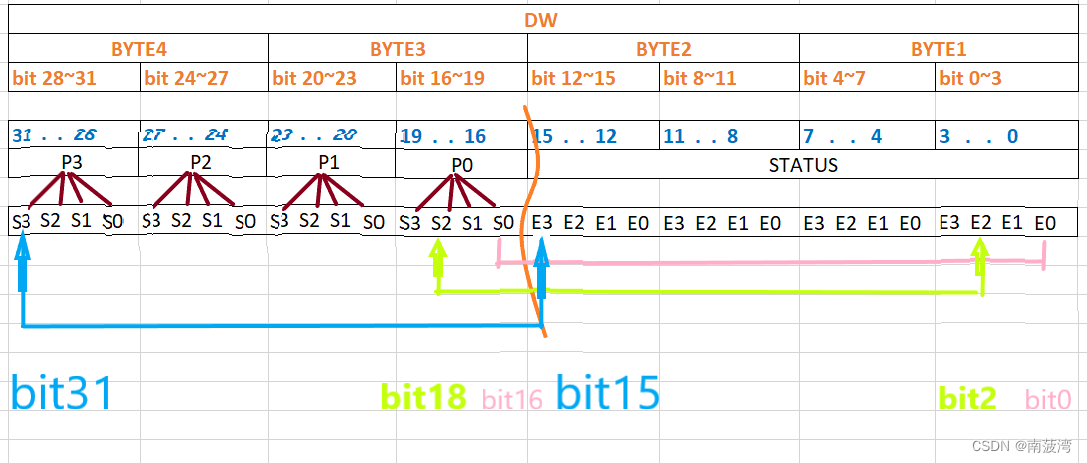
Pose2 SLAM
Pose2 SLAM是一种昂进行同时定位与地图构建(SLAM)的一种简单方法是仅仅融合连续机器人姿态之间的相对姿态测量。这种不涉及地标的SLAM变体通常被称为 "Pose SLAM"。
%pip -q install gtbook # also installs latest gtsam pre-releaseNote: you may need to restart the kernel to use updated packages.
import math
import gtsam
import gtsam.utils.plot as gtsam_plot
import matplotlib.pyplot as pltPRIOR_NOISE = gtsam.noiseModel.Diagonal.Sigmas(gtsam.Point3(0.3, 0.3, 0.1))
ODOMETRY_NOISE = gtsam.noiseModel.Diagonal.Sigmas(
gtsam.Point3(0.2, 0.2, 0.1))1.创建一个因子图容器并向其中添加因子。
graph = gtsam.NonlinearFactorGraph()2. 在第一个姿态上添加一个先验,将其设置为原点。
一个先验因子由一个均值和一个噪声(协方差矩阵)组成,使用 ODOMETRY_NOISE。
在因子图优化中,"先验"(Prior)是指对某个变量的先验知识或约束。在SLAM问题中,您可以通过添加先验来设置某个变量的初始值或初始不确定性。在这里,希望对第一个姿态设置一个先验,将其设置为原点。
graph.add(gtsam.PriorFactorPose2(1, gtsam.Pose2(0, 0, 0), PRIOR_NOISE))3. 添加里程计(Odometry)因子 在连续姿态之间创建里程计(Between)因子。
在SLAM中,里程计因子(Odometry Factors)用于表示机器人在连续时间步之间的相对运动估计,通常基于传感器数据如里程计、IMU等。这些因子可以帮助系统获得更准确的姿态估计和地图构建,特别是在没有其他传感器或约束的情况下。
graph.add(gtsam.BetweenFactorPose2(1, 2, gtsam.Pose2(2, 0, 0), ODOMETRY_NOISE))
graph.add(gtsam.BetweenFactorPose2(2, 3, gtsam.Pose2(2, 0, math.pi / 2), ODOMETRY_NOISE))
graph.add(gtsam.BetweenFactorPose2(3, 4, gtsam.Pose2(2, 0, math.pi / 2), ODOMETRY_NOISE))
graph.add(gtsam.BetweenFactorPose2(4, 5, gtsam.Pose2(2, 0, math.pi / 2),ODOMETRY_NOISE))4. 添加闭环约束
这个因子编码了我们已经返回到相同姿态的事实。在实际系统中,可以通过多种方式识别这些约束,例如使用相机图像的基于外观的技术。我们将使用另一个 Between 因子来强制执行这个约束。
graph.add( gtsam.BetweenFactorPose2(5, 2, gtsam.Pose2(2, 0, math.pi / 2), ODOMETRY_NOISE))
print("\nFactor Graph:\n{}".format(graph))5.创建数据结构来保存初始估计值以供解决方案使用。
为了说明目的,这些初始值故意设置为不正确的值。
initial_estimate = gtsam.Values()
initial_estimate.insert(1, gtsam.Pose2(0.5, 0.0, 0.2))
initial_estimate.insert(2, gtsam.Pose2(2.3, 0.1, -0.2))
initial_estimate.insert(3, gtsam.Pose2(4.1, 0.1, math.pi / 2))
initial_estimate.insert(4, gtsam.Pose2(4.0, 2.0, math.pi))
initial_estimate.insert(5, gtsam.Pose2(2.1, 2.1, -math.pi / 2))
print("\nInitial Estimate:\n{}".format(initial_estimate)) 6.优化初始值使用 Gauss-Newton 非线性优化器。
该优化器可以接受一组可选的配置参数,用于控制收敛准则、线性系统求解器的类型以及在优化过程中显示的信息量等。我们将设置一些参数作为演示。
parameters = gtsam.GaussNewtonParams()在优化过程中,如果连续两步之间的误差变化小于某个阈值,可以选择停止迭代。
parameters.setRelativeErrorTol(1e-5)不要执行超过 N 步迭代
parameters.setMaxIterations(100)Create the optimizer ...
optimizer = gtsam.GaussNewtonOptimizer(graph, initial_estimate, parameters)... and optimize
result = optimizer.optimize()
print("Final Result:\n{}".format(result))7.计算并打印所有变量的边际协方差
marginals = gtsam.Marginals(graph, result)
for i in range(1, 6):
print("X{} covariance:\n{}\n".format(i, marginals.marginalCovariance(i)))for i in range(1, 6):
gtsam_plot.plot_pose2(0, result.atPose2(i), 0.5,
marginals.marginalCovariance(i))
plt.axis('equal')
plt.show()结果展示
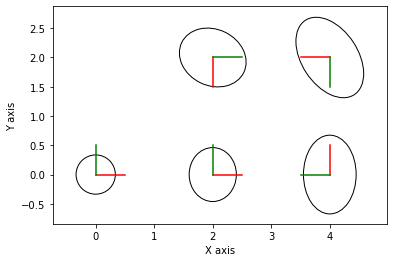

![[C++] string类的介绍与构造的模拟实现,进来看吧,里面有空调](https://img-blog.csdnimg.cn/a746a3bdb3db4521a78cc094207f94ed.gif#pic_center)