一、简介

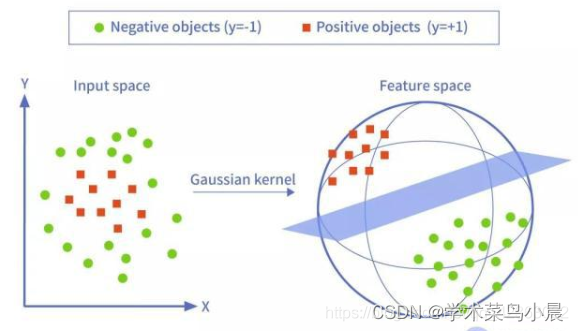
SVM是一种二类分类模型，在特征空间中寻找间隔最大的分离超平面，使得数据得到高效的二分类。

 二、SVM损失函数

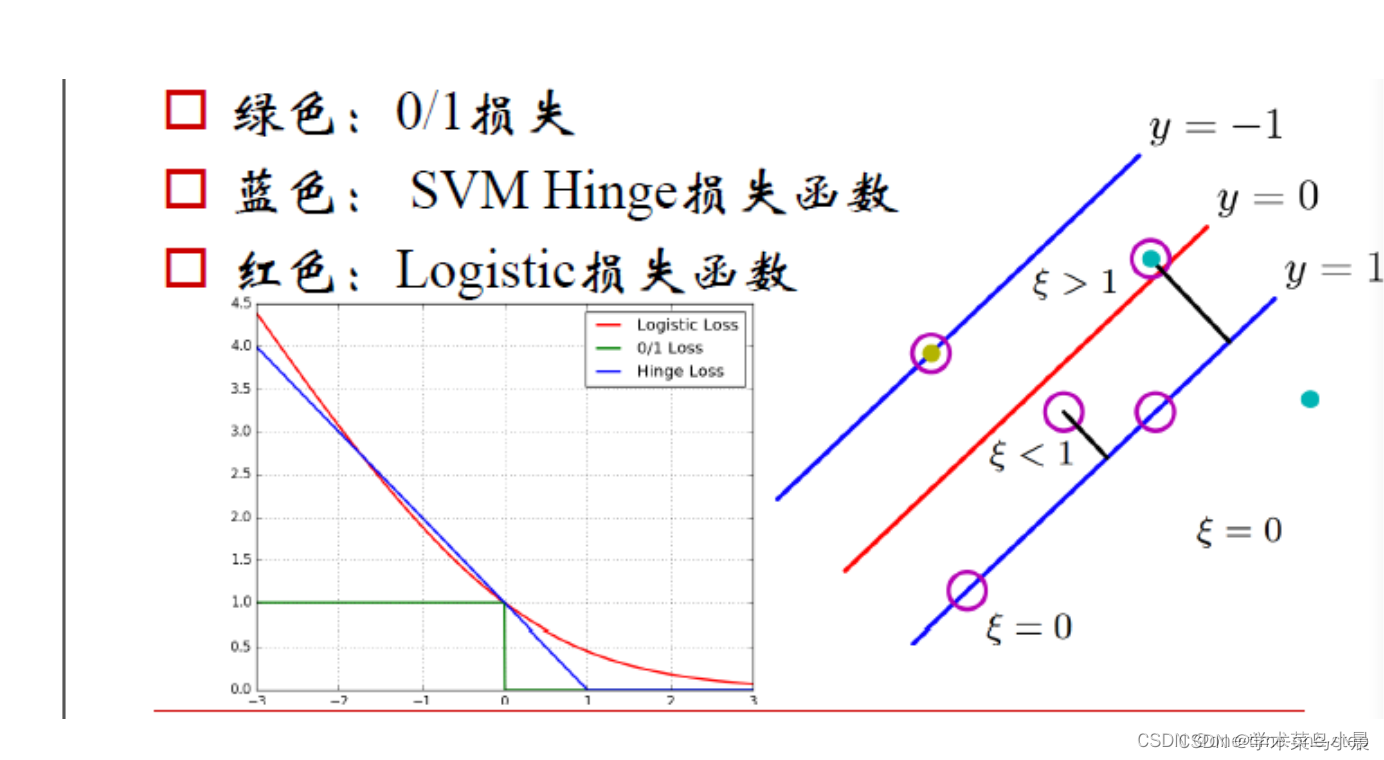
SVM 的三种损失函数衡量模型的性能。

  1. 0-1 损失：
        当正例样本落在 y=0 下方则损失为 0，否则损失为 1.
        当负例样本落在 y=0 上方则损失为0，否则损失为 1.
   2.  Hinge （合页）损失：
        当正例落在 y >= 1 一侧则损失为0，否则距离越远则损失越大.
        当负例落在 y <= -1 一侧则损失为0，否则距离越远则损失越大.
   3. Logistic 损失：
        当正例落在 y > 0 一侧，并且距离 y=0 越远则损失越小.
        当负例落在 y < 0 一侧，并且距离 y=0 越远则损失越小.

 

当存在线性不可分的场景时，我们需要使用核函数来提高训练样本的维度、或者将训练样本投向高维，SVM 默认使用 RBF 核函数，将低维空间样本投射到高维空间，再寻找分割超平面。

• SVM的优点：

  • 在高维空间中非常高效；
  • 即使在数据维度比样本数量大的情况下仍然有效；

• SVM的缺点：

  • 如果特征数量比样本数量大得多，在选择核函数时要避免过拟合；

  • 对缺失数据敏感;

  • 对于核函数的高维映射解释力不强