矩阵

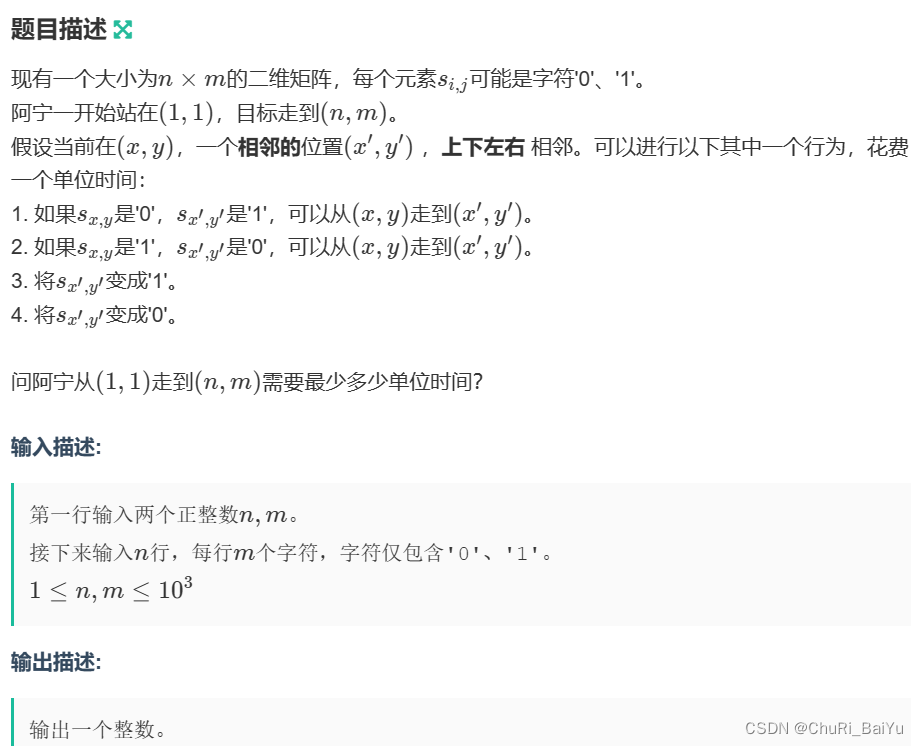
问题建模

给定一个n*m的字符矩阵，字符矩阵内包含两种字符’0’和’1’，从（1,1)出发，每次可以花费一单位时间向上下左右移动，若要到达格子与当前格子的字符不同则可以走到该位置，若不同可以花费一单位时间修改要到达格子的字符，才能走到，问到达（n,m）所需的最短单位时间为多少。

问题分析

1.分析所求

从(1,1)到(n,m)的最短时间问题，可以通过跑bfs的最短路来得到。由于相邻格子间能否移动与格子上的字符有关，则可以采用分层图，来维护格子上为不同字符时，所得到的最短距离，最终取到终点的最短距离即可。

代码

#include<bits/stdc++.h>

#define x first
#define y second
#define C(i) str[0][i]!=str[1][i]
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
const int N =1e3+10,INF=0x3f3f3f3f;
string g[N];
int d[N][N][2];///两层的状态图
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int n,m;
struct Node{
    int x,y,c;
};


void bfs(){
    memset(d,INF,sizeof(d));
    queue<Node> q;
    q.push({0,0,g[0][0]-'0'});
    d[0][0][g[0][0]-'0']=0;

    while(q.size()){
        auto qt=q.front();
        q.pop();
        int x=qt.x,y=qt.y;
        for(int i=0;i<4;i++){
            int nx=x+dx[i],ny=y+dy[i];
            if(nx<0||nx>=n||ny<0||ny>=m)    continue;
            ///若从当前点到达目标点的距离更短，则更新目标点最短距离
            if(d[nx][ny][qt.c^1]>d[x][y][qt.c]+1+(g[nx][ny]-'0'==qt.c)){
                d[nx][ny][qt.c^1]=d[x][y][qt.c]+1+(g[nx][ny]-'0'==qt.c);
                q.push({nx,ny,qt.c^1});
            }
        }
    }
}

void solve() {
    cin >>n >>m;
    for(int i=0;i<n;i++)    cin >>g[i];
    bfs();
    cout <<min(d[n-1][m-1][0],d[n-1][m-1][1]) <<"\n";
}


int main() {
    int t = 1;
    //cin >> t;
    while (t--) solve();
    return 0;
}