53. Maximum Subarray
题意:一个数组,找到和最大的子串
我的思路
我记得好像On的动态规划来做的?但是想不起来了,先死做,用的前缀和——TLE超时
那就只能想想dp怎么做了
假设dp[i]表示的是以 i 为右端点的最大的子串,dp[0]是自己;
i=1时,如果dp[0]小于0,dp[1]=nums[1],否则dp[1]=dp[0]+nums[1]
i=2时,如果dp[1]小于0,dp[2]=nums[2],否则dp[2]=dp[2-1]+nums[2]
所以状态转移方程为:如果dp[i - 1]小于0,dp[ i ]=nums[ i ],否则dp[ i ]=dp[i -1]+nums[ i ]
On解决,同时dp换成nums还能更省空间
代码 Runtime 87 ms Beats 78.76% Memory67.9 MB Beats 8.86%
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n=nums.size();
int maxx=nums[0];
for(int i=1;i<n;i++){
if(nums[i-1]>0) nums[i]=nums[i]+nums[i-1];
maxx=max(maxx,nums[i]);
}
return maxx;
}
};如果想跟快的话,取消同步 Runtime 50 ms Beats 99.91% Memory 67.7 MB Beats 81.53%
class Solution {
public:
int maxSubArray(vector<int>& nums) {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int n=nums.size();
int maxx=nums[0];
for(int i=1;i<n;i++){
if(nums[i-1]>0) nums[i]=nums[i]+nums[i-1];
maxx=max(maxx,nums[i]);
}
return maxx;
}
};标答补充 分治
看看分治的代码
分成左右中三个部分,左边部分是左边最大的子串和,右边部分得到右边最大字串和;
左边部分是所有包含了m-1位置的字符串的最大子串和 lmax,右边部分是包含了m+1位置的字符串的最大字串和 rmax,返回max(lmax. rmax ),ml+mr+nums[m]两者之中大的那一个
代码 Runtime110 ms Beats 65.10% Memory 67.9 MB Beats 8.86%
class Solution {
public:
int maxSubArray(vector<int>& nums) {
return maxSubArray(nums, 0, nums.size() - 1);
}
private:
int maxSubArray(vector<int>& nums, int l, int r) {
if (l > r) return INT_MIN;
int m = l + (r - l) / 2, ml = 0, mr = 0;
int lmax = maxSubArray(nums, l, m - 1);
int rmax = maxSubArray(nums, m + 1, r);
for (int i = m - 1, sum = 0; i >= l; i--) {
sum += nums[i];
ml = max(sum, ml);
}
for (int i = m + 1, sum = 0; i <= r; i++) {
sum += nums[i];
mr = max(sum, mr);
}
return max(max(lmax, rmax), ml + mr + nums[m]);
}
};54. Spiral Matrix
题意: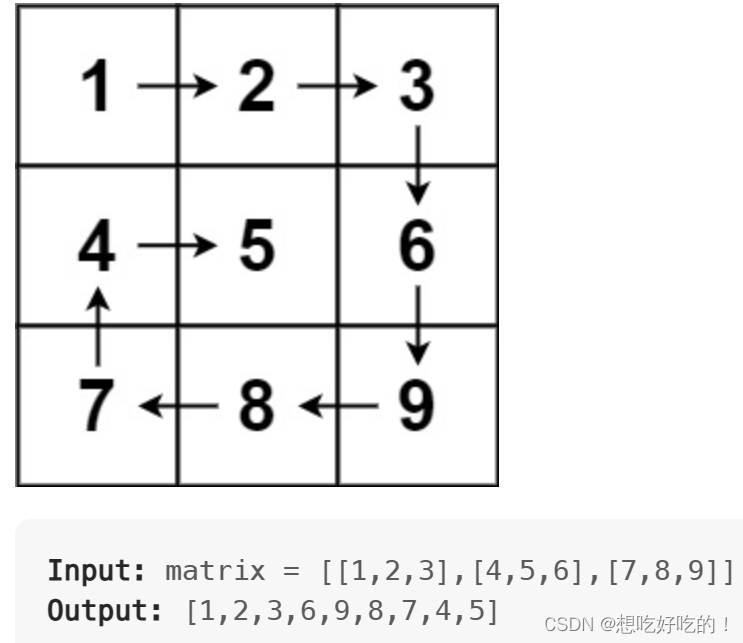
我的思路
死做
代码 Runtime 0 ms Beats 100% Memory6.9 MB Beats 61.55%
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int dy[]={1, 0,-1,0};
int dx[]={0, 1, 0,-1};
bool vis[19][19]={0};
int m=matrix.size(),n=matrix[0].size();
int nowx=0,nowy=0,mod=0;
int nx=0,ny=0;
vector<int> ans;
for(int i=0;i<m*n;i++){//首先循环一开始的新来的一定是可以的
nowx=nx,nowy=ny;
vis[nowx][nowy]=1;
ans.push_back(matrix[nowx][nowy]);
if(i+1==m*n)break;
nx=nowx+dx[mod];ny=nowy+dy[mod];
while(nx<0||nx>=m||ny<0||ny>=n||vis[nx][ny]==1){
mod=(mod+1)%4;nx=nowx+dx[mod];ny=nowy+dy[mod];
}
}
return ans;
}
};55. Jump Game
题意:问能不能从索引0到索引n-1
我的思路
既然是问能不能到到终点,用贪心或者动态规划都可以,上次用了动态规划,这次就贪心吧
注意:记得 if(nums[0]==0&&n!=1)return 0;要特判
代码 Runtime 43 ms Beats 93.40% Memory48.3 MB Beats 74.51%
class Solution {
public:
bool canJump(vector<int>& nums) {
int n=nums.size();
if(nums[0]==0&&n!=1)return 0;
for(int i=1;i<n-1;i++){
nums[i]=max(nums[i]+i,nums[i-1]);
if(nums[i]==i)return 0;
}
return 1;
}
};56. Merge Intervals
题意:返回重叠部分

我的思路
应该是要维护两端端点的,好像是-1 +1什么的?
做着做着发现这个interval还有start==end,这个-1和+1怎么做??
点的话就找一个bool数组特判吧
代码 Runtime19 ms Beats 99.65% Memory19.2 MB Beats 31.70%
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& in) {
int vis[10004]={0};int n=in.size();int maxx=0;
bool fl[10004]={0};//判点
vector<vector<int>> ans;
for(int i=0;i<n;i++){
int st=in[i][0],en=in[i][1];
maxx=max(maxx,en);
if(st==en)fl[st]=1;
else vis[st]++,vis[en]--;
}
int st=0,en=0,sum=0;
int mod=1;//mod1是找正数,找到正数了切换mod-1找负数
for(int i=0;i<=maxx;i++){
sum=sum+vis[i];
if(mod==1&&sum>0){st=i;mod=-mod;}
else if(mod==-1&&sum==0){
en=i;mod=-mod;
ans.push_back({st,en});
}
else if(fl[i]&&mod==1){
ans.push_back({i,i});
}
}
return ans;
}
};标答 排序
标答的时间复杂度为O(n+logn)
首先将interval排序,应该是按照覆盖的起点排序,起点从小到大排序;
遍历每个覆盖域,首先是第一个覆盖区域,初始化start和end;之后不断地找大的end,直到目前最大的end小于新来的start,这时把起点和重点放到答案列表中,更新起点和终点
代码 Runtime 23 ms Beats 98.10% Memory19 MB Beats 71.5%
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> ans;
int n=intervals.size();
sort(intervals.begin(),intervals.end());
int start=intervals[0][0];
int end=intervals[0][1];
for(int i=1;i<n;i++){
if(end<intervals[i][0]){
ans.push_back({start,end});
start=intervals[i][0];
end=intervals[i][1];
}
else{
end=max(intervals[i][1],end);
}
}
ans.push_back({start,end});
return ans;
}
};62. Unique Paths
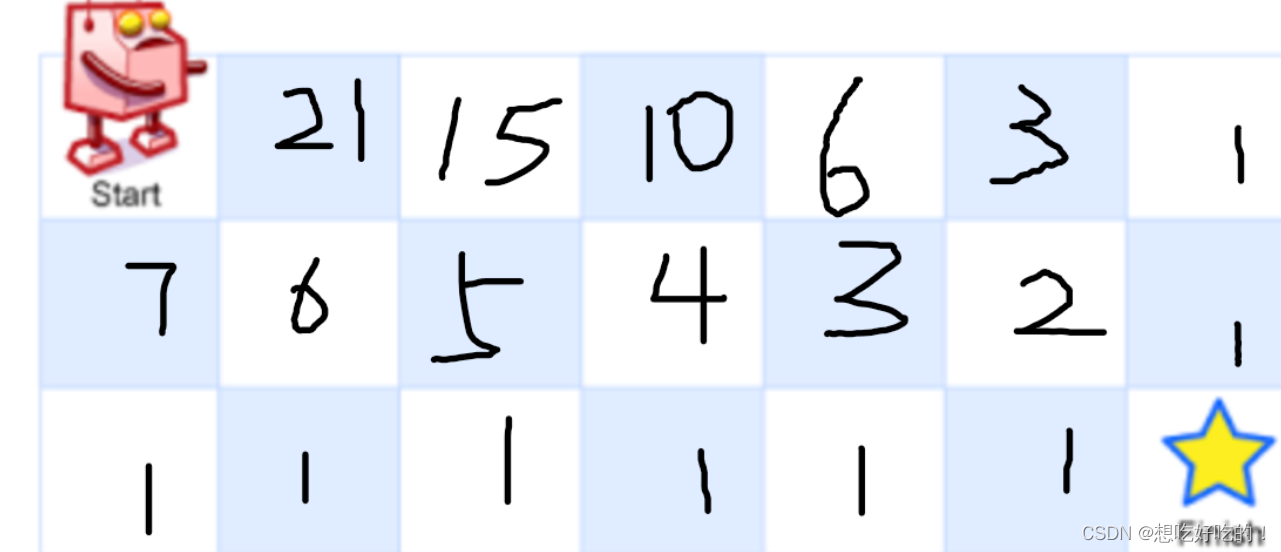
题意:机器人只能向下或者向右走,要从grid[0][0]走到grid[m-1][n-1]
我的思路
好像是组合数?按按计算器看看能不能推出来,没推出来
好像递归也是能够做出来的?不过走楼梯是一维的c[i+1]+c[i+2]得到的?
那么假设c是方案数,就先按照下面这个图建立一个二维数组做?
【看标答,这种方法居然是dp】
代码 Runtime 0 ms Beats 100% Memory6 MB Beats 87.9%
class Solution {
public:
int uniquePaths(int m, int n) {
int st[104][104]={0};st[m-1][n-1]=1;
for(int i=m-1;i>=0;i--)
for(int j=n-1;j>=0;j--)
st[i][j]+=(st[i+1][j]+st[i][j+1]);
return st[0][0];
}
};标答 组合数
在这个图上,一共要走m+n-2步,其中有m-1步是向下的,n-1步是向右的,这可以转换成m-1个向下和n-1个向右的排序(图源知乎)

代码 Runtime 0 ms Beats 100.00% Memory 6 MB Beats 87.9%
class Solution {
public:
int uniquePaths(int m, int n) {
int N = n+m-2; // total steps = n-1 + m-1
int r = min(n,m)-1;
// will iterate on the minimum for efficiency = (total) C (min(right, down)
double res = 1;// compute nCr
for(int i=1; i<=r; ++i, N--)
res = res*(N)/i;
return (int)res;
}
};64. Minimum Path Sum
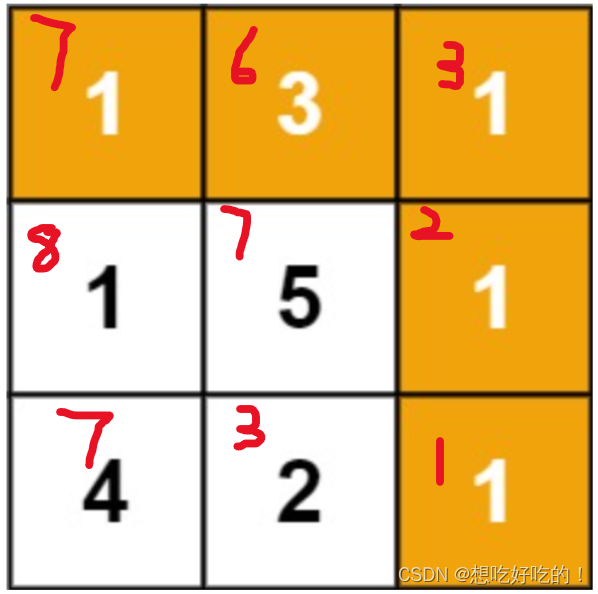
题意:二维地图,只能向下或者向右走,找到所有路径上的最小的值。
我的思路
这个肯定是dp吧;还是相同的道理,但是要注意边缘处理
dp[i][j]=num[i][j]+min(dp[i+1][j],dp[i][j+1])
代码 Runtime 6 ms Beats 88.72% Memory 9.7 MB Beats 89.19%
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m=grid.size(),n=grid[0].size();
for(int i=m-1;i>=0;i--){
for(int j=n-1;j>=0;j--){
if(i==m-1 && j==n-1)continue;
if(i==m-1)grid[i][j]+=grid[i][j+1];
else if(j==n-1)grid[i][j]+=grid[i+1][j];
else grid[i][j]+=min(grid[i+1][j],grid[i][j+1]);
}
}
return grid[0][0];
}
};70. Climbing Stairs
题意:爬楼梯,只能走1或2步,问到终点要走多少步
我的思路
n=1,c=1;n=2,c=2;n=3,c=3;c[i]=c[i-1]+c[i-2]
代码 Runtime 0 ms Beats 100% Memory 5.9 MB Beats 94.85%
class Solution {
public:
int climbStairs(int n) {
if(n<3) return n;
int a=1,b=2,c=0;
for(int i=3;i<=n;i++){
c=a+b;a=b;b=c;
}
return c;
}
};72. Edit Distance
题意:三个操作:插入一个字母,删除一个字母,替换一个字母;问从字符串1变成字符串2最少需要多少步?
我的思路
应该是用动态规划
假设