BitMap的存储原理

1. bitMap他会标识出某个整数是否存在，存在即为1，不存在对应位即为0
2. bitMap是存储int类型的，int = 4byte， 1byte = 8bit，因此bitMap数组中的每个下标可以标识出32个数字是否存在
3. bitMap相当于一个个小格子，底层是一个int类型数组，数组的每个下标可以存储32个数字，如果bitMap的长度设置为100，则可以标识出100 * 32 = 3200 个数字是否存在
4. 假设现在有数字【0， 10， 24， 50】那么0会保存到下标为0的那个位，10会保存下标为10的位置，24会保存下标是24的位置，50会保存下标是50的位置，即假设bitMap中第 30个位置对应值 = 1， 则表示30这个数字是存在的
5. bitMap不能存储【负数,float,double】等非正整数的数字。
6. bitMap以32位的倍数出现，即我们要存50这个数字，则bitMap总共size就是64，因为50大于32，但小于64，所以需要两个空间存储，即size = 64
7. bitSet是java中的类型，他的底层是Long存储的，所以它是以64位为一个整体，bitSet中每个数组位可以标识64个数字，同理也不能出现【负数,fload, double】类型
8. 注意：bitMap可以标识字符串和对象，但是必须要先进行hash取模，然后再存，由于是hash取模，所以存储字符串 或 对象会出现hash碰撞，导致不准确的情况出现

BitMap 与 BitSet的使用场景

1. 用户签到登录，签到的用户根据自增id，在对应位上打上1的标识
2. 统计uv，即有多少人访问了网站，把访问网站的用户id打到对应标识位上置1， 最后统计bitMap中为1的个数即可
3. 领取优惠券，每人只能领取1次，领取的人把id打到对应bitMap位置上置1，领取前根据该用户id查询bitMap是否为1，如果为1，则直接拒绝，因为已经领取了

java中BitSet的使用方式及常用API

package bitmap;


import java.util.BitSet;

/**
 * 要求： 有1千万个随机数，分布在1 到 1亿之间，需要找出1 到 1亿不存在的数据，即随机剩下的9千万数据
 *
 * 使用java的bitSet集合
 *
 * bitSet是Long类型，每一个组是64bit
 * bitMap是int类型，每一个组32bit
 *
 * 注意：bitSet不能存负数，只能存0以上的并且在Long类型范围内的正整数
 */
public class BitSetTest {

    public static void main(String[] args) {

        // 这个初始化128，会在里面生成一个128个桶的Long类型的数组，所以一共有128 * 64 个bit位，也就是一共能标记出128 * 64个整数是否存在
        // 不指定默认64
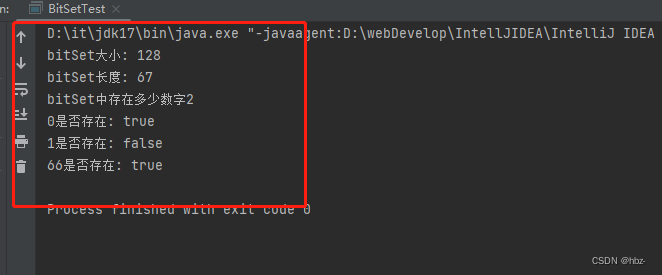
        BitSet bitSet = new BitSet(128);
        bitSet.set(0);
        bitSet.set(66);


        // 输出bitSet大小，应该是128，因为66大于64，所以需要第二个Long位，每个Long位是64，2个就是128
        System.out.println("bitSet大小: " + bitSet.size());
        // 这个是bit位的长度，是最大的那个数字+1，即67
        System.out.println("bitSet长度: " + bitSet.length());
        // 查询出有多少个为1的位，显然我们只存了0和66，只有俩，所以结果就是2
        System.out.println("bitSet中存在多少数字" + bitSet.cardinality());
        // 读取bit位 = 0的下标， 返回true，说明存数据了，即该位的值 = 1，因为bitSet.set(0)，
        // 把0存到了第0位，这是必然的，0一定是存到下标位0的位置，这是规则，不需要认为指定
        System.out.println("0是否存在: " + bitSet.get(0));
        // 读取bit位 = 1的下标，返回false， 说明该位没有存数据，即没有存数字1，所以该位的值 = 0， 表示1这个数字不存在
        System.out.println("1是否存在: " + bitSet.get(1));
        System.out.println("66是否存在: " + bitSet.get(66));


    }
}

输出：

布隆过滤器

1. 布隆过滤器可以支持多种类型，而bitSet 和 bitMap只能支持正整数
2. 布隆过滤器本身不支持删除元素，因为可能出现好几个值由于hash碰撞都存到了同一个格子，如果删除可能会影响到其他元素。
3. 当然可以把布隆过滤器改造成带有计数的效果，即如果某个格子计数是1，即只有一个元素占有这个位置，这个时候就可以删除
4. 布隆过滤器保存某个值的时候可以通过多次hash，比如把"java"进行3次不同的hash算法取模，会得到3个不同的hash值，那么这3个值都会保存到布隆过滤器对应的位中，即"java"这个值会被存到3个位置，这3个位置都标记这"java"的hash
5. 布隆过滤器说没有，那一定就不存在；但是布隆过滤器说存在，那未必真的存在，因为可能发生hash碰撞，导致你要查的元素hash的值和别的元素hash值相同了，这个时候布隆过滤器会误判成存在

布隆过滤器是如何降低误判

1. 保存元素时，会对该元素去多个hash值，把这些hash值全部存到布隆过滤器中(比如要存"java"， 进行3次hash后值分别是【2,10,26】, 那么"java"这个值就会被同时存储到【2, 10, 26】的位置)
2. 当要查询一个元素是否存在时，会以同样的hash算法计算出3个值，然后用这3个值去布隆过滤器的对应3个位置去找，如果这3个位置有一个位置是0，则直接判该值不存在(假如之前只存了"java"， 现在要查询"web"这个字符串是否存在， 那么会以同样的hash算法对"web"进行3次hash取模，假如取到的是【2, 15, 26】, 会发现15这个位置是0，此时直接回判定"web"不存在，尽管2, 26都有，但15没有，就说明"web"不存在)
3. 当布隆过滤器中的bit格子被逐渐被占满时候，此时即使hash取3个值，依然会有大概率误判，因为可能hash出来的3个值都和其他元素发生hash碰撞了(比如要查询"cloud", 取模是【10, 15, 26】, 而布隆过滤器并没有"cloud"， 而10, 15, 26却都是1，因为与"java", “web"发生hash碰撞了，所以会误判"cloud"也存在，而实际却并不存在"cloud”)