1.快速排序的基本过程

快速排序是分治法运用到排序问题的典型例子，基本思想是：通过一个标记pivot元素将n个元素的序列划分为左右两个子序列left和right，其中left中的元素都比pivot小，right的都比pivot的大，然后再次对left和right各自再执行快速排序，第一次的pivot不参与，将左右子序列运用同样的方法排序，知道最后剩余一个元素的时候结束，（其中的pivot这里用数组中间的元素）。

双指针移动：

left: arr[left] < pivot时，不移动，arr[left] > pivot时，left++

right: arr[right] > pivot时，不移动，否则，right--

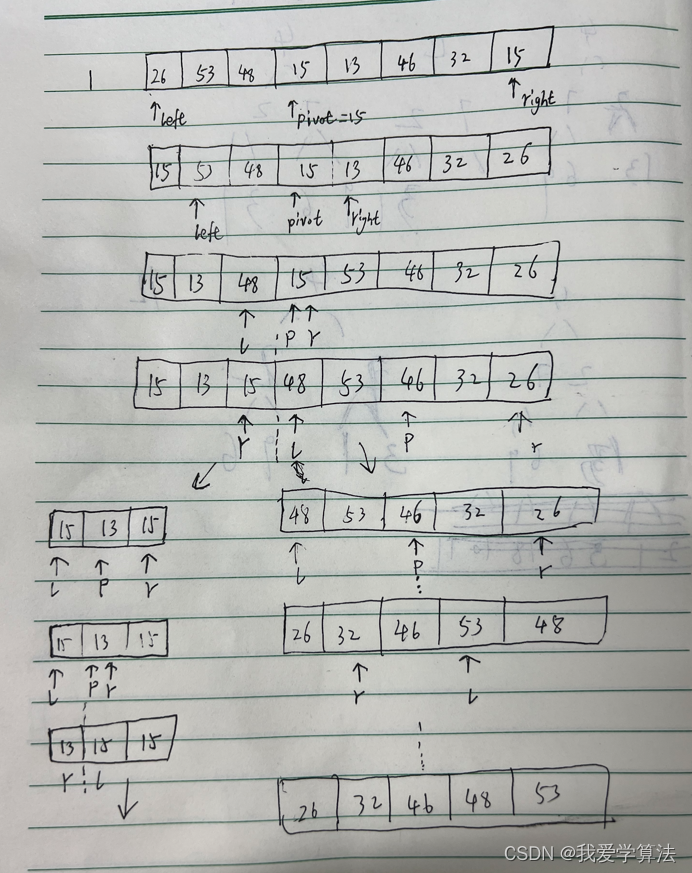
代码实现：

    public void quickSort(int[] arr,int start,int end){
        if (start >= end){
            return;
        }
        //这里就是一个对撞的双指针
        int left = start,right = end;
        int pivot = arr[(start + end) / 2];
        while (left <= right){
            while (left <= right && arr[left] < pivot){
                left++;
            }
            while (left <= right && arr[right] > pivot){
                right--;
            }
            if (left <= right){
                int temp = arr[left];
                arr[left] = arr[right];
                arr[right] = temp;
                left++;
                right--;
            }
        }
        //分别处理其左右部分
        //此时的left和right在pivot的两边
        quickSort(arr,start,right);
        quickSort(arr,left,end);
    }

复杂度分析：

如果我们每次选的pivot每次都正好在中间，效率时最高的，但是这是无法保证的，因此我们需要从最好、最坏和中间情况来分析。