来源：力扣（LeetCode）

描述：

给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。

给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。

请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

示例 1：

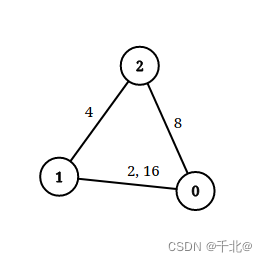
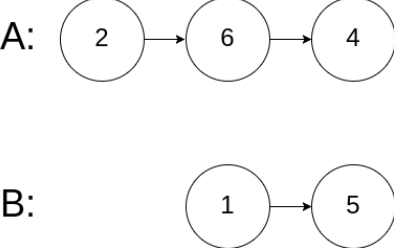
输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出：[false,true]
解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16 。
对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。
对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。

示例 2：

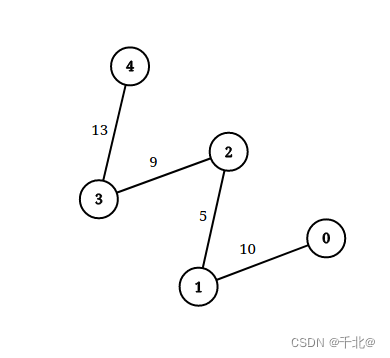
输入：n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出：[true,false]
解释：上图为给定数据。

提示：

• 2 <= n <= 10⁵
• 1 <= edgeList.length, queries.length <= 10⁵
• edgeList[i].length == 3
• queries[j].length == 3
• 0 <= ui, vi, pj, qj <= n - 1
• ui != vi
• pj != qj
• 1 <= disi, limitj <= 10⁹
• 两个点之间可能有 多条 边。

前言

  关于并查集的详细说明可以参考 OI Wiki「并查集」或者 LeetBook「并查集」，本文不作过多说明。

方法：离线查询 + 并查集

  给定一个查询时，我们可以遍历 edgeList 中的所有边，依次将长度小于 limit 的边加入到并查集中，然后使用并查集查询 p 和 q 是否属于同一个集合。如果 p 和 q 属于同一个集合，则说明存在从 p 到 q 的路径，且这条路径上的每一条边的长度都严格小于 limit，查询返回 true，否则查询返回 false。

  如果 queries 的 limit 是非递减的，显然上一次查询的并查集里的边都是满足当前查询的 limit 要求的，我们只需要将剩余的长度小于 limit 的边加入并查集中即可。基于此，我们首先将 edgeList 按边长度从小到大进行排序，然后将 queries 按 limit 从小到大进行排序，使用 k 指向上一次查询中不满足 limit 要求的长度最小的边，显然初始时 k = 0。

  我们依次遍历 queries：如果 k 指向的边的长度小于对应查询的 limit，则将该边加入并查集中，然后将 k 加 1，直到 k 指向的边不满足要求；最后根据并查集查询对应的 p 和 q 是否属于同一集合来保存查询的结果。

代码：

class Solution {
public:
    int find(vector<int> &uf, int x) {
        if (uf[x] == x) {
            return x;
        }
        return uf[x] = find(uf, uf[x]);
    }

    void merge(vector<int> &uf, int x, int y) {
        x = find(uf, x);
        y = find(uf, y);
        uf[y] = x;
    }

    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
        sort(edgeList.begin(), edgeList.end(), [](vector<int> &e1, vector<int> &e2) {
            return e1[2] < e2[2];
        });

        vector<int> index(queries.size());
        iota(index.begin(), index.end(), 0);
        sort(index.begin(), index.end(), [&](int i1, int i2) {
            return queries[i1][2] < queries[i2][2];
        });

        vector<int> uf(n);
        iota(uf.begin(), uf.end(), 0);
        vector<bool> res(queries.size());
        int k = 0;
        for (auto i : index) {
            while (k < edgeList.size() && edgeList[k][2] < queries[i][2]) {
                merge(uf, edgeList[k][0], edgeList[k][1]);
                k++;
            }
            res[i] = find(uf, queries[i][0]) == find(uf, queries[i][1]);
        }
        return res;
    }
};

执行用时：440 ms, 在所有 C++ 提交中击败了96.64%的用户
内存消耗：107.6 MB, 在所有 C++ 提交中击败了80.54%的用户
复杂度分析
时间复杂度：O(ElogE+mlogm+(E+m)logn+n)，其中 E 是 edgeList 的长度，m 是 queriesqueries 的长度，n 是点数。对 edgeList 和 queries 进行排序分别需要 O(ElogE) 和 O(mlogm)，并查集初始化需要 O(n)，并查集查询和合并总共需要 O((E+m)logn)。
空间复杂度：O(logE+m+n)。保存并查集需要 O(n) 的空间，保存 index 需要 O(m) 的空间，以及排序需要的栈空间。
author：LeetCode-Solution