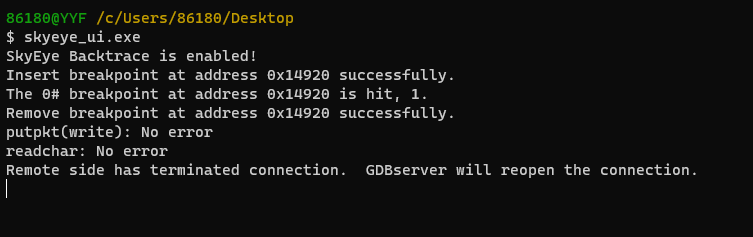
分析：

        补题， 首先大体思路就是先算一遍没改变任何点时能够买到的物品，这一步可以通过看两点之间距离，之间能够包含几个d就说明会需要买几次物品，对于两侧边界，可以将左侧设置为1 - d， 因为此时可以计算第一个到1之间需不需要买，最后一个数设置为n + 1，就可以计算最后一个点到离开之间需不需要买，可以认为找的两点之间的距离是包括前一个点不包括后一个点的，这样每次只会处理一个点。然后枚举每一个点，判断移动这个点会产生什么影响，a = (s[i] - s[i - 1] - 1) / d也就是这个点到前一个点的距离之间需要买几次，b = (s[i + 1] - s[i] - 1) / d是这个点的后一个点到这个点的距离之间需要买几次，c = (s[i + 1] - s[i - 1] - 1) / d是不看这个点看两侧的点之间需要买几次，也就是移动这个点后的买的次数，用c - (a + b)就可以得到移动当前的点会产生的变化差值，然后总的买的次数还需要加上剩余的m - 1个点，对每一个得到的答案都取最小值，在找到有多少个最小值，就可以得出答案。

代码：

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

typedef pair<int, int> pii;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int T;
    cin >> T;
    while(T --) {
        ll n, d;
        int m;
        cin >> n >> m >> d;
        vector<int> s(m + 2);
        s[0] = 1 - d;
        s[m + 1] = n + 1;
        for(int i = 1; i <= m; i ++) cin >> s[i];
        int sum = 0;
        for(int i = 1; i <= m + 1; i ++) {
            sum += (s[i] - s[i - 1] - 1) / d;
        }
        int ans = n + 1;
        int cnt = 0;
        for(int i = 1; i <= m; i ++) {
            int t = sum;
            int a = (s[i] - s[i - 1] - 1) / d;
            int b = (s[i + 1] - s[i] - 1) / d;
            int c = (s[i + 1] - s[i - 1] - 1) / d;
            t += (c - (a + b));
            t += (m - 1);
            if(ans > t) {
                ans = t;
                cnt = 1;
            }
            else if(ans == t) cnt ++;
        }
        cout << ans << ' ' << cnt << '\n';
    }
}