1，理论

最简单的方式利用向量进行求解

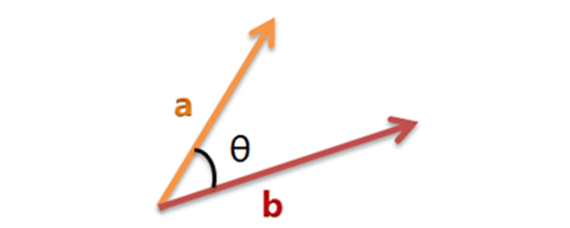
 如图可得：

cosθ=a*b/（|a|*|b|）

已知三点坐标，很容易可以得到两向量之积a*b，以及每个的模值

2，四个角度求解过程

1. 首先，我们定义了四个坐标点pointA、pointB、pointC、pointD，这些点构成了一个四边形。

2. 接下来，我们调用calculateAngle方法来计算四边形的每个内角。calculateAngle方法接受三个参数，分别是三个点的坐标，用于计算夹角。

3. 在calculateAngle方法中，我们首先计算向量1的x和y分量，即点p1与点p2之间的向量。然后计算向量2的x和y分量，即点p3与点p2之间的向量。

4. 接着，我们计算向量1和向量2的点积，即dotProduct = vector1x * vector2x + vector1y * vector2y。

5. 计算向量1和向量2的模，即各自的长度，使用Math.sqrt()方法计算平方根。

6. 接下来，我们计算夹角的余弦值，即cosTheta = dotProduct / (magnitude1 * magnitude2)。

7. 最后，我们使用Math.acos()方法计算夹角的弧度值，并将其转换为度数，使用Math.toDegrees()方法。

8. 在main方法中，我们依次计算四边形的四个内角，并将其打印输出。

3，代码实现

import java.awt.geom.Point2D;

public class QuadrilateralAngles {
    public static void main(String[] args) {
        // 四个坐标点
        Point2D.Double pointA = new Point2D.Double(0, 0);
        Point2D.Double pointB = new Point2D.Double(1, 1);
        Point2D.Double pointC = new Point2D.Double(0, 1);
        Point2D.Double pointD = new Point2D.Double(-1, 0);

        // 计算四边形的四个内角
        double angleA = calculateAngle(pointD, pointA, pointB);
        double angleB = calculateAngle(pointA, pointB, pointC);
        double angleC = calculateAngle(pointB, pointC, pointD);
        double angleD = calculateAngle(pointC, pointD, pointA);

        // 输出结果
        System.out.println("Angle A: " + angleA);
        System.out.println("Angle B: " + angleB);
        System.out.println("Angle C: " + angleC);
        System.out.println("Angle D: " + angleD);
    }

    // 计算夹角的方法
    public static double calculateAngle(Point2D.Double p1, Point2D.Double p2, Point2D.Double p3) {
        // 计算向量1的x和y分量
        double vector1x = p1.getX() - p2.getX();
        double vector1y = p1.getY() - p2.getY();

        // 计算向量2的x和y分量
        double vector2x = p3.getX() - p2.getX();
        double vector2y = p3.getY() - p2.getY();

        // 计算向量1和向量2的点积
        double dotProduct = vector1x * vector2x + vector1y * vector2y;

        // 计算向量1和向量2的模
        double magnitude1 = Math.sqrt(vector1x * vector1x + vector1y * vector1y);
        double magnitude2 = Math.sqrt(vector2x * vector2x + vector2y * vector2y);

        // 计算两向量夹角的余弦值
        double cosTheta = dotProduct / (magnitude1 * magnitude2);

        // 计算夹角的弧度值
        double theta = Math.acos(cosTheta);

        // 将弧度转换为度数并返回
        return Math.toDegrees(theta);
    }
}