图片来源:作者
一、说明
图形神经网络 (GNN) 代表了深度学习领域最迷人、发展最迅速的架构之一。作为旨在处理结构化为图形的数据的深度学习模型,GNN 带来了非凡的多功能性和强大的学习能力。
在各种类型的GNN中,图卷积网络(GCN)已成为最普遍和应用最广泛的模型。GCN具有创新性,因为它们能够利用节点的特征及其局部性进行预测,从而提供了一种处理图形结构数据的有效方法。
在本文中,我们将深入研究GCN层的机制并解释其内部工作原理。此外,我们将探索它在节点分类任务中的实际应用,使用 PyTorch 几何作为我们选择的工具。
PyTorch Geometric 是 PyTorch 的专用扩展,专为开发和实现 GNN 而创建。它是一个先进但用户友好的库,提供了一套全面的工具来促进基于图形的机器学习。要开始我们的旅程,将需要 PyTorch 几何安装。如果你使用的是Google Colab,PyTorch应该已经到位,所以我们需要做的就是执行一些额外的命令。
所有代码都可以在Google Colab和GitHub上找到。
!pip install torch_geometricimport torch
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt现在安装了 PyTorch 几何,让我们探索一下我们将在本教程中使用的数据集。
二、🌐 I. 图形数据
图形是表示对象之间关系的基本结构。您可以在多种现实场景中遇到图形数据,例如社交和计算机网络、分子的化学结构、自然语言处理和图像识别等。
在本文中,我们将研究臭名昭著且广泛使用的 Zachary 空手道俱乐部数据集。

图片来源:作者
Zachary的空手道俱乐部数据集体现了Wayne W. Zachary在1970年代观察到的空手道俱乐部内形成的关系。它是一种社交网络,其中每个节点代表一个俱乐部成员,节点之间的边缘代表在俱乐部环境之外发生的交互。
在这种特殊情况下,俱乐部的成员被分成四个不同的组。我们的任务是根据每个成员的交互模式为每个成员分配正确的组(节点分类)。
让我们使用 PyG 的内置函数导入数据集,并尝试理解它使用的对象。Datasets
from torch_geometric.datasets import KarateClub# Import dataset from PyTorch Geometric
dataset = KarateClub()
# Print information
print(dataset)
print('------------')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')KarateClub()
------------
Number of graphs: 1
Number of features: 34
Number of classes: 4 此数据集只有 1 个图,其中每个节点都有一个 34 维的特征向量,并且是四个类(我们的四个组)中的一个的一部分。实际上,该对象可以被视为(图形)对象的集合。DatasetsData
我们可以进一步检查我们独特的图表以了解更多信息。
# Print first element
print(f'Graph: {dataset[0]}')Graph: Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34]) 该对象特别有趣。打印它提供了我们正在研究的图表的一个很好的总结:Data
x=[34, 34]是具有形状(节点数、特征数)的节点特征矩阵。在我们的例子中,这意味着我们有 34 个节点(我们的 34 个成员),每个节点都与一个 34 暗的特征向量相关联。edge_index=[2, 156]表示图形连通性(节点的连接方式)与形状(2,有向边的数量)。y=[34]是节点地面真实标签。在这个问题中,每个节点都被分配给一个类(组),所以我们每个节点都有一个值。train_mask=[34]是一个可选属性,它通过 OR 语句列表告知哪些节点应该用于训练。TrueFalse
让我们打印这些张量中的每一个,以了解它们存储的内容。让我们从节点功能开始。
data = dataset[0]print(f'x = {data.x.shape}')
print(data.x)x = torch.Size([34, 34])
tensor([[1., 0., 0., ..., 0., 0., 0.],
[0., 1., 0., ..., 0., 0., 0.],
[0., 0., 1., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 1., 0., 0.],
[0., 0., 0., ..., 0., 1., 0.],
[0., 0., 0., ..., 0., 0., 1.]]) 在这里,节点特征矩阵是一个单位矩阵:它不包含有关节点的任何相关信息。它可以包含年龄、技能水平等信息,但在此数据集中并非如此。这意味着我们必须通过查看节点的连接来对节点进行分类。x
现在,让我们打印边缘索引。
print(f'edge_index = {data.edge_index.shape}')
print(data.edge_index)edge_index = torch.Size([2, 156])
tensor([[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3,
3, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7,
7, 7, 8, 8, 8, 8, 8, 9, 9, 10, 10, 10, 11, 12, 12, 13, 13, 13,
13, 13, 14, 14, 15, 15, 16, 16, 17, 17, 18, 18, 19, 19, 19, 20, 20, 21,
21, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 25, 25, 25, 26, 26, 27, 27,
27, 27, 28, 28, 28, 29, 29, 29, 29, 30, 30, 30, 30, 31, 31, 31, 31, 31,
31, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33,
33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33],
[ 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 17, 19, 21, 31, 0, 2,
3, 7, 13, 17, 19, 21, 30, 0, 1, 3, 7, 8, 9, 13, 27, 28, 32, 0,
1, 2, 7, 12, 13, 0, 6, 10, 0, 6, 10, 16, 0, 4, 5, 16, 0, 1,
2, 3, 0, 2, 30, 32, 33, 2, 33, 0, 4, 5, 0, 0, 3, 0, 1, 2,
3, 33, 32, 33, 32, 33, 5, 6, 0, 1, 32, 33, 0, 1, 33, 32, 33, 0,
1, 32, 33, 25, 27, 29, 32, 33, 25, 27, 31, 23, 24, 31, 29, 33, 2, 23,
24, 33, 2, 31, 33, 23, 26, 32, 33, 1, 8, 32, 33, 0, 24, 25, 28, 32,
33, 2, 8, 14, 15, 18, 20, 22, 23, 29, 30, 31, 33, 8, 9, 13, 14, 15,
18, 19, 20, 22, 23, 26, 27, 28, 29, 30, 31, 32]]) 在图论和网络分析中,节点之间的连接使用各种数据结构进行存储。这是一种这样的数据结构,其中图形的连接存储在两个列表中(156 条有向边,相当于 78 条双向边)。这两个列表的原因是,一个列表存储源节点,而第二个列表标识目标节点。edge_index
此方法称为坐标列表 (COO) 格式,本质上是一种有效存储稀疏矩阵的方法。稀疏矩阵是有效存储具有大多数零元素的矩阵的数据结构。在COO格式中,仅存储非零元素,从而节省内存和计算资源。
相反,表示图形连通性的更直观和直接的方法是通过邻接矩阵 A。这是一个方阵,其中每个元素 Aij s 都表示图中从节点 i 到节点 j 的边是否存在。换句话说,非零元素 Aij 表示从节点 i 到节点 j 的连接,零表示没有直接连接。
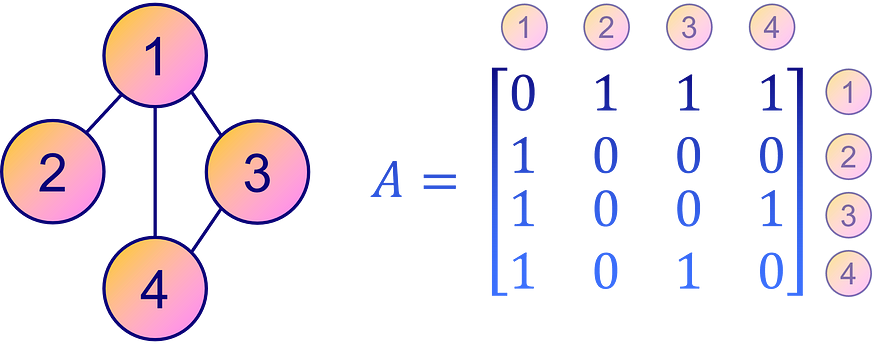
图片来源:作者
但是,邻接矩阵不如稀疏矩阵或边较少的图形的 COO 格式节省空间。但是,为了清晰和易于解释,邻接矩阵仍然是表示图形连通性的常用选择。
邻接矩阵可以从 与效用函数 推断。edge_indexto_dense_adj()
from torch_geometric.utils import to_dense_adjA = to_dense_adj(data.edge_index)[0].numpy().astype(int)
print(f'A = {A.shape}')
print(A)A = (34, 34)
[[0 1 1 ... 1 0 0]
[1 0 1 ... 0 0 0]
[1 1 0 ... 0 1 0]
...
[1 0 0 ... 0 1 1]
[0 0 1 ... 1 0 1]
[0 0 0 ... 1 1 0]]对于图形数据,节点密集互连的情况相对较少见。如您所见,我们的邻接矩阵 A 是稀疏的(用零填充)。
在许多真实世界的图形中,大多数节点仅连接到少数其他节点,导致邻接矩阵中出现大量零。存储这么多零根本没有效率,这就是 PyG 采用 COO 格式的原因。
相反,真实标签很容易理解。
print(f'y = {data.y.shape}')
print(data.y)y = torch.Size([34])
tensor([1, 1, 1, 1, 3, 3, 3, 1, 0, 1, 3, 1, 1, 1, 0, 0, 3, 1, 0, 1, 0, 1, 0, 0,
2, 2, 0, 0, 2, 0, 0, 2, 0, 0]) 我们存储的节点真实标签只是对每个节点的组号(0、1、2、3)进行编码,这就是为什么我们有 34 个值的原因。y
最后,让我们打印训练掩模。
print(f'train_mask = {data.train_mask.shape}')
print(data.train_mask)train_mask = torch.Size([34])
tensor([ True, False, False, False, True, False, False, False, True, False,
False, False, False, False, False, False, False, False, False, False,
False, False, False, False, True, False, False, False, False, False,
False, False, False, False])训练掩码显示哪些节点应该用于语句训练。这些节点代表训练集,而其他节点可以视为测试集。该部门通过提供看不见的测试数据来帮助模型评估。True
但我们还没有完成!该物体还有很多东西可以提供。它提供了各种实用函数,可以研究图形的多个属性。例如:数据
Datais_directed()告诉您图形是否定向。有向图表示邻接矩阵不对称,即边的方向在节点之间的连接中很重要。isolated_nodes()检查某些节点是否未连接到图形的其余部分。由于缺乏连接,这些节点可能会在分类等任务中带来挑战。has_self_loops()指示是否至少有一个节点连接到自身。这与循环的概念不同:循环意味着在同一节点开始和结束的路径,遍历其间的其他节点。
在Zachary的空手道俱乐部数据集的上下文中,所有这些属性都返回 。这意味着图形不是定向的,没有任何孤立的节点,并且它的任何节点都没有连接到自身。False
print(f'Edges are directed: {data.is_directed()}')
print(f'Graph has isolated nodes: {data.has_isolated_nodes()}')
print(f'Graph has loops: {data.has_self_loops()}')Edges are directed: False
Graph has isolated nodes: False
Graph has loops: False 最后,我们可以使用 将图形从 PyTorch 几何转换为流行的图形库 NetworkX。这对于使用 和 可视化小图特别有用。to_networkxnetworkxmatplotlib
让我们为每个组使用不同的颜色绘制数据集。
from torch_geometric.utils import to_networkxG = to_networkx(data, to_undirected=True)
plt.figure(figsize=(12,12))
plt.axis('off')
nx.draw_networkx(G,
pos=nx.spring_layout(G, seed=0),
with_labels=True,
node_size=800,
node_color=data.y,
cmap="hsv",
vmin=-2,
vmax=3,
width=0.8,
edge_color="grey",
font_size=14
)
plt.show()
Zachary 空手道俱乐部的这块图显示了我们的 34 个节点、78 条(双向)边缘和 4 个带有 4 种不同颜色的标签。现在我们已经了解了使用 PyTorch Geometric 加载和处理数据集的基本要素,我们可以介绍图卷积网络架构。
三、✉️ 第二。图卷积网络
本节旨在从头开始介绍和构建图卷积层。
在传统的神经网络中,线性层对传入的数据应用线性变换。此变换通过使用权重矩阵 W 将输入特征 x 转换为隐藏向量 h。暂时忽略偏见,这可以表示为:
![]()
对于图形数据,通过节点之间的连接增加了额外的复杂性层。这些连接很重要,因为通常,在网络中,假设相似的节点比不同的节点更有可能相互链接,这种现象被称为网络同质。
我们可以通过将其特征与其邻居的特征合并来丰富节点表示。此操作称为卷积或邻域聚合。让我们将节点 i 的邻域表示为,包括它自己为 Ñ。

与卷积神经网络(CNN)中的过滤器不同,我们的权重矩阵W是唯一的,并且在每个节点之间共享。但还有另一个问题:节点不像像素那样有固定数量的邻居。
我们如何解决一个节点只有一个邻居,而另一个节点有 500 个邻居的情况?如果我们简单地对特征向量求和,对于具有 500 个邻居的节点,生成的嵌入 h 会大得多。为了确保所有节点的值范围相似以及它们之间的可比性,我们可以根据节点的程度对结果进行归一化,其中度是指节点具有的连接数。
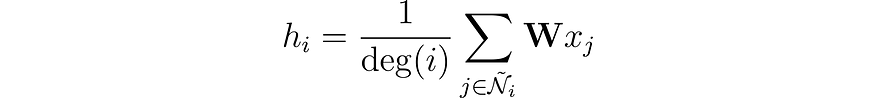
我们快到了!由Kipf等人(2016)引入,图卷积层有一个最终的改进。
作者观察到,来自具有众多邻居的节点的特征比来自更孤立节点的特征更容易传播。为了抵消这种影响,他们建议为来自相邻节点较少的特征分配更大的权重,从而平衡所有节点的影响。此操作编写为:

请注意,当 i 和 j 具有相同数量的邻居时,它相当于我们自己的层。现在,让我们看看如何使用PyTorch Geometric在Python中实现它。
四、🧠 第三。实现 GCN
PyTorch Geometric 提供了直接实现图卷积层的功能。GCNConv
在此示例中,我们将创建一个基本的图卷积网络,其中包含单个 GCN 层、一个 ReLU 激活函数和一个线性输出层。此输出层将生成对应于我们的四个类别的四个值,最高值确定每个节点的类。
在下面的代码块中,我们用一个三维隐藏层定义GCN层。
from torch.nn import Linear
from torch_geometric.nn import GCNConvclass GCN(torch.nn.Module):
def __init__(self):
super().__init__()
self.gcn = GCNConv(dataset.num_features, 3)
self.out = Linear(3, dataset.num_classes)
def forward(self, x, edge_index):
h = self.gcn(x, edge_index).relu()
z = self.out(h)
return h, z
model = GCN()
print(model)GCN(
(gcn): GCNConv(34, 3)
(out): Linear(in_features=3, out_features=4, bias=True)
)
如果我们添加第二个 GCN 层,我们的模型不仅会聚合来自每个节点的邻居的特征向量,还会聚合来自这些邻居的邻居的特征向量。
我们可以堆叠几个图形层来聚合越来越远的值,但有一个问题:如果我们添加太多层,聚合会变得如此强烈,以至于所有嵌入最终看起来都一样。这种现象称为过度平滑,当您的图层过多时,这可能是一个真正的问题。
现在我们已经定义了我们的GNN,让我们用PyTorch编写一个简单的训练循环。我选择了常规的交叉熵损失,因为它是一个多类分类任务,以 Adam 作为优化器。在本文中,我们不会实现训练/测试拆分以保持简单,而是专注于 GNN 的学习方式。
训练循环是标准的:我们尝试预测正确的标签,并将 GCN 的结果与存储在 中的值进行比较。误差是通过交叉熵损失计算的,并与亚当反向传播,以微调GNN的权重和偏差。最后,我们每 10 个时期打印一次指标。data.y
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.02)# Calculate accuracy
def accuracy(pred_y, y):
return (pred_y == y).sum() / len(y)
# Data for animations
embeddings = []
losses = []
accuracies = []
outputs = []
# Training loop
for epoch in range(201):
# Clear gradients
optimizer.zero_grad()
# Forward pass
h, z = model(data.x, data.edge_index)
# Calculate loss function
loss = criterion(z, data.y)
# Calculate accuracy
acc = accuracy(z.argmax(dim=1), data.y)
# Compute gradients
loss.backward()
# Tune parameters
optimizer.step()
# Store data for animations
embeddings.append(h)
losses.append(loss)
accuracies.append(acc)
outputs.append(z.argmax(dim=1))
# Print metrics every 10 epochs
if epoch % 10 == 0:
print(f'Epoch {epoch:>3} | Loss: {loss:.2f} | Acc: {acc*100:.2f}%')Epoch 0 | Loss: 1.40 | Acc: 41.18%
Epoch 10 | Loss: 1.21 | Acc: 47.06%
Epoch 20 | Loss: 1.02 | Acc: 67.65%
Epoch 30 | Loss: 0.80 | Acc: 73.53%
Epoch 40 | Loss: 0.59 | Acc: 73.53%
Epoch 50 | Loss: 0.39 | Acc: 94.12%
Epoch 60 | Loss: 0.23 | Acc: 97.06%
Epoch 70 | Loss: 0.13 | Acc: 100.00%
Epoch 80 | Loss: 0.07 | Acc: 100.00%
Epoch 90 | Loss: 0.05 | Acc: 100.00%
Epoch 100 | Loss: 0.03 | Acc: 100.00%
Epoch 110 | Loss: 0.02 | Acc: 100.00%
Epoch 120 | Loss: 0.02 | Acc: 100.00%
Epoch 130 | Loss: 0.02 | Acc: 100.00%
Epoch 140 | Loss: 0.01 | Acc: 100.00%
Epoch 150 | Loss: 0.01 | Acc: 100.00%
Epoch 160 | Loss: 0.01 | Acc: 100.00%
Epoch 170 | Loss: 0.01 | Acc: 100.00%
Epoch 180 | Loss: 0.01 | Acc: 100.00%
Epoch 190 | Loss: 0.01 | Acc: 100.00%
Epoch 200 | Loss: 0.01 | Acc: 100.00%伟大!毫不意外地,我们在训练集(完整数据集)上达到了 100% 的准确率。这意味着我们的模型学会了正确地将空手道俱乐部的每个成员分配到正确的小组。
我们可以通过对图形进行动画处理来生成整洁的可视化效果,并在训练过程中查看GNN预测的演变。
%%capture
from IPython.display import HTML
from matplotlib import animation
plt.rcParams["animation.bitrate"] = 3000def animate(i):
G = to_networkx(data, to_undirected=True)
nx.draw_networkx(G,
pos=nx.spring_layout(G, seed=0),
with_labels=True,
node_size=800,
node_color=outputs[i],
cmap="hsv",
vmin=-2,
vmax=3,
width=0.8,
edge_color="grey",
font_size=14
)
plt.title(f'Epoch {i} | Loss: {losses[i]:.2f} | Acc: {accuracies[i]*100:.2f}%',
fontsize=18, pad=20)
fig = plt.figure(figsize=(12, 12))
plt.axis('off')
anim = animation.FuncAnimation(fig, animate, \
np.arange(0, 200, 10), interval=500, repeat=True)
html = HTML(anim.to_html5_video())
display(html)
最初的预测是随机的,但 GCN 会在一段时间后完美地标记每个节点。事实上,最终的图表与我们在第一部分末尾绘制的图表相同。但是GCN真正学到了什么?
通过聚合来自相邻节点的特征,GNN学习网络中每个节点的向量表示(或嵌入)。在我们的模型中,最后一层只是学习如何使用这些表示来生成最佳分类。然而,嵌入是GNN的真正产物。
让我们打印模型学习的嵌入。
# Print embeddings
print(f'Final embeddings = {h.shape}')
print(h)Final embeddings = torch.Size([34, 3])
tensor([[1.9099e+00, 2.3584e+00, 7.4027e-01],
[2.6203e+00, 2.7997e+00, 0.0000e+00],
[2.2567e+00, 2.2962e+00, 6.4663e-01],
[2.0802e+00, 2.8785e+00, 0.0000e+00],
[0.0000e+00, 0.0000e+00, 2.9694e+00],
[0.0000e+00, 0.0000e+00, 3.3817e+00],
[0.0000e+00, 1.5008e-04, 3.4246e+00],
[1.7593e+00, 2.4292e+00, 2.4551e-01],
[1.9757e+00, 6.1032e-01, 1.8986e+00],
[1.7770e+00, 1.9950e+00, 6.7018e-01],
[0.0000e+00, 1.1683e-04, 2.9738e+00],
[1.8988e+00, 2.0512e+00, 2.6225e-01],
[1.7081e+00, 2.3618e+00, 1.9609e-01],
[1.8303e+00, 2.1591e+00, 3.5906e-01],
[2.0755e+00, 2.7468e-01, 1.9804e+00],
[1.9676e+00, 3.7185e-01, 2.0011e+00],
[0.0000e+00, 0.0000e+00, 3.4787e+00],
[1.6945e+00, 2.0350e+00, 1.9789e-01],
[1.9808e+00, 3.2633e-01, 2.1349e+00],
[1.7846e+00, 1.9585e+00, 4.8021e-01],
[2.0420e+00, 2.7512e-01, 1.9810e+00],
[1.7665e+00, 2.1357e+00, 4.0325e-01],
[1.9870e+00, 3.3886e-01, 2.0421e+00],
[2.0614e+00, 5.1042e-01, 2.4872e+00],
...
[2.1778e+00, 4.4730e-01, 2.0077e+00],
[3.8906e-02, 2.3443e+00, 1.9195e+00],
[3.0748e+00, 0.0000e+00, 3.0789e+00],
[3.4316e+00, 1.9716e-01, 2.5231e+00]], grad_fn=<ReluBackward0>)如您所见,嵌入不需要具有与特征向量相同的维度。在这里,我选择将维度的数量从 34 () 减少到 3,以获得漂亮的 <>D 可视化效果。dataset.num_features
让我们在任何训练发生之前绘制这些嵌入,在纪元 0 处。
# Get first embedding at epoch = 0
embed = h.detach().cpu().numpy()fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot(projection='3d')
ax.patch.set_alpha(0)
plt.tick_params(left=False,
bottom=False,
labelleft=False,
labelbottom=False)
ax.scatter(embed[:, 0], embed[:, 1], embed[:, 2],
s=200, c=data.y, cmap="hsv", vmin=-2, vmax=3)
plt.show()
我们看到Zachary空手道俱乐部的每个节点都有它们的真实标签(而不是模型的预测)。目前,他们到处都是,因为GNN还没有经过训练。但是,如果我们在训练循环的每一步绘制这些嵌入,我们将能够可视化GNN真正学到的东西。
让我们看看它们是如何随着时间的推移而演变的,因为GCN在对节点进行分类方面变得越来越好。
%%capturedef animate(i):
embed = embeddings[i].detach().cpu().numpy()
ax.clear()
ax.scatter(embed[:, 0], embed[:, 1], embed[:, 2],
s=200, c=data.y, cmap="hsv", vmin=-2, vmax=3)
plt.title(f'Epoch {i} | Loss: {losses[i]:.2f} | Acc: {accuracies[i]*100:.2f}%',
fontsize=18, pad=40)
fig = plt.figure(figsize=(12, 12))
plt.axis('off')
ax = fig.add_subplot(projection='3d')
plt.tick_params(left=False,
bottom=False,
labelleft=False,
labelbottom=False)
anim = animation.FuncAnimation(fig, animate, \
np.arange(0, 200, 10), interval=800, repeat=True)
html = HTML(anim.to_html5_video())
display(html)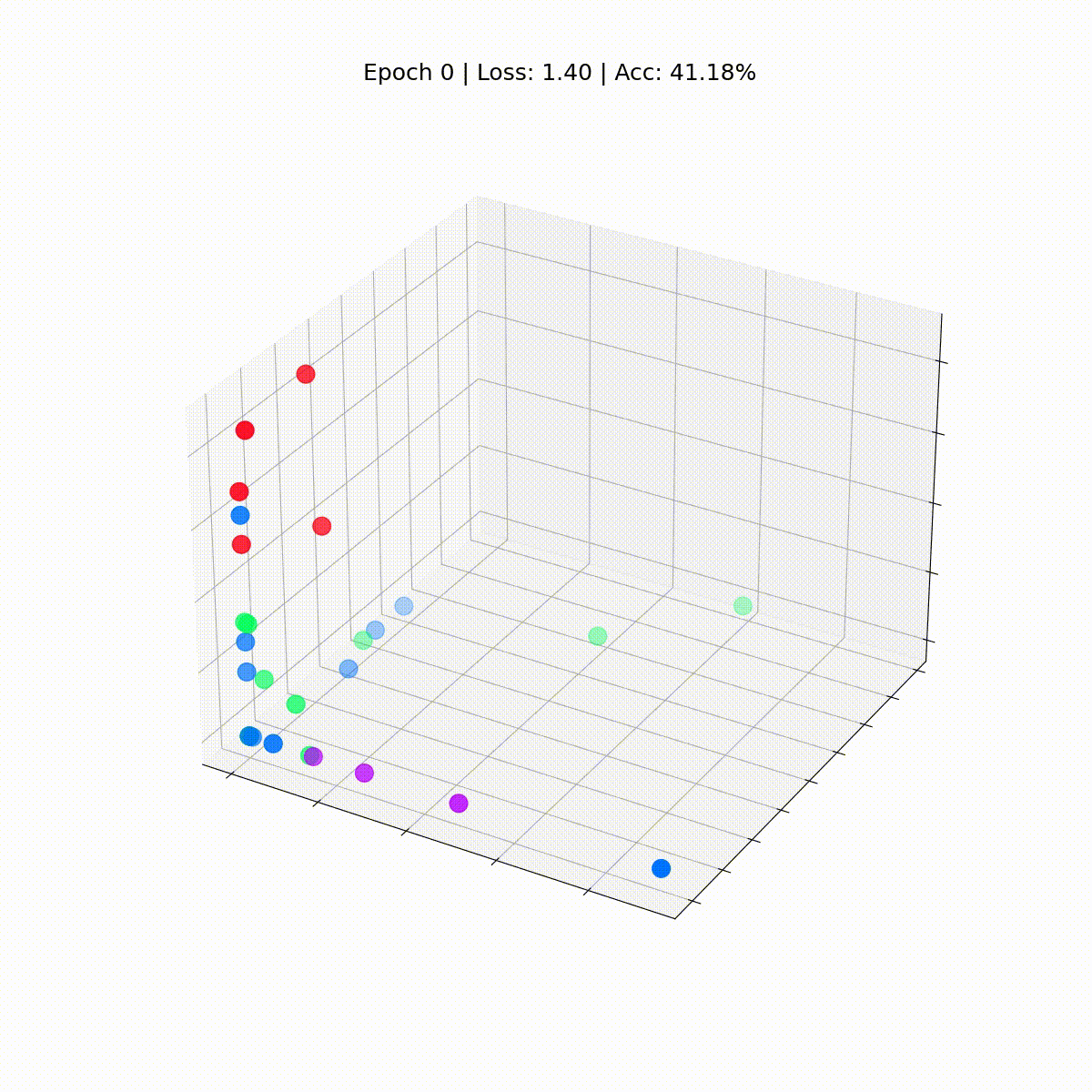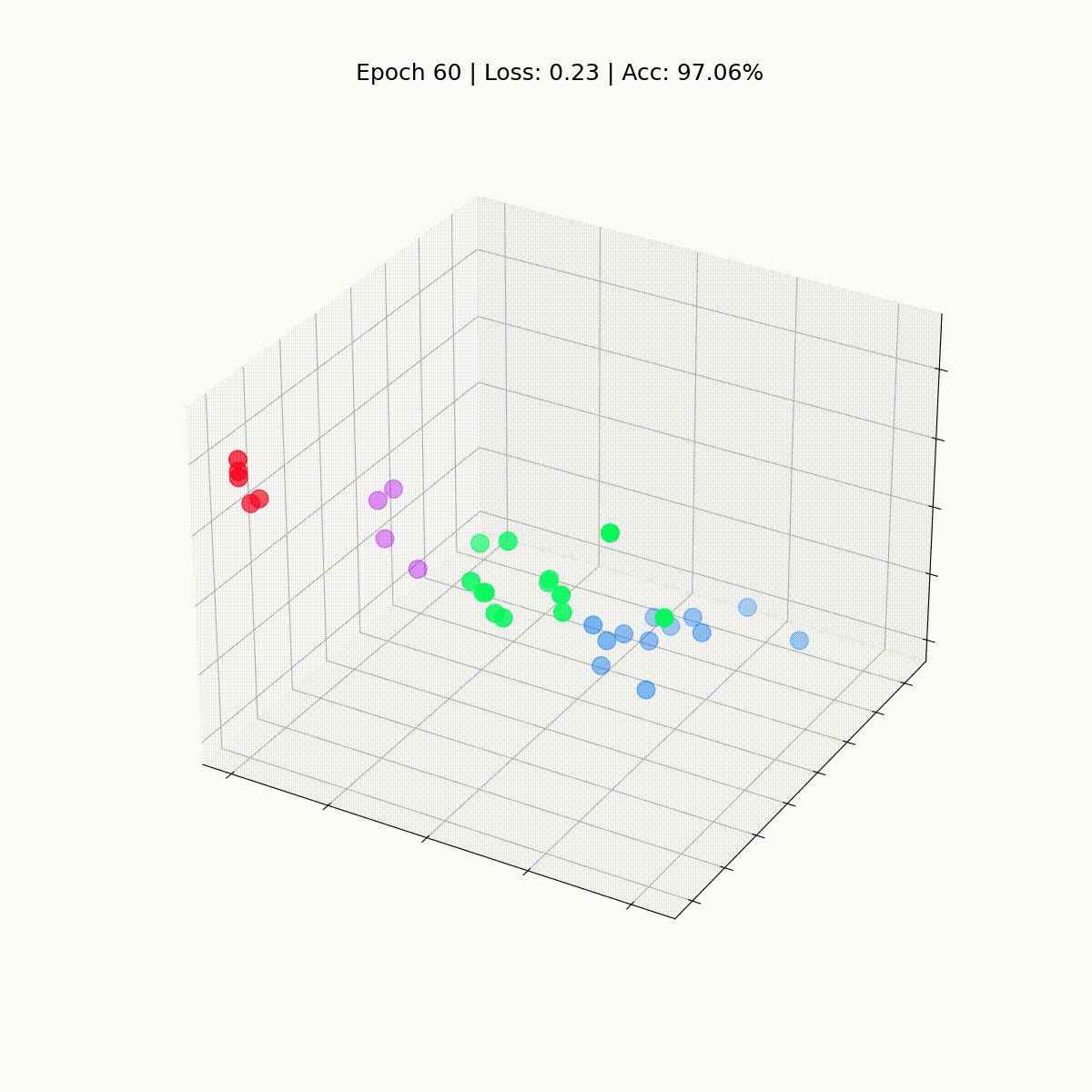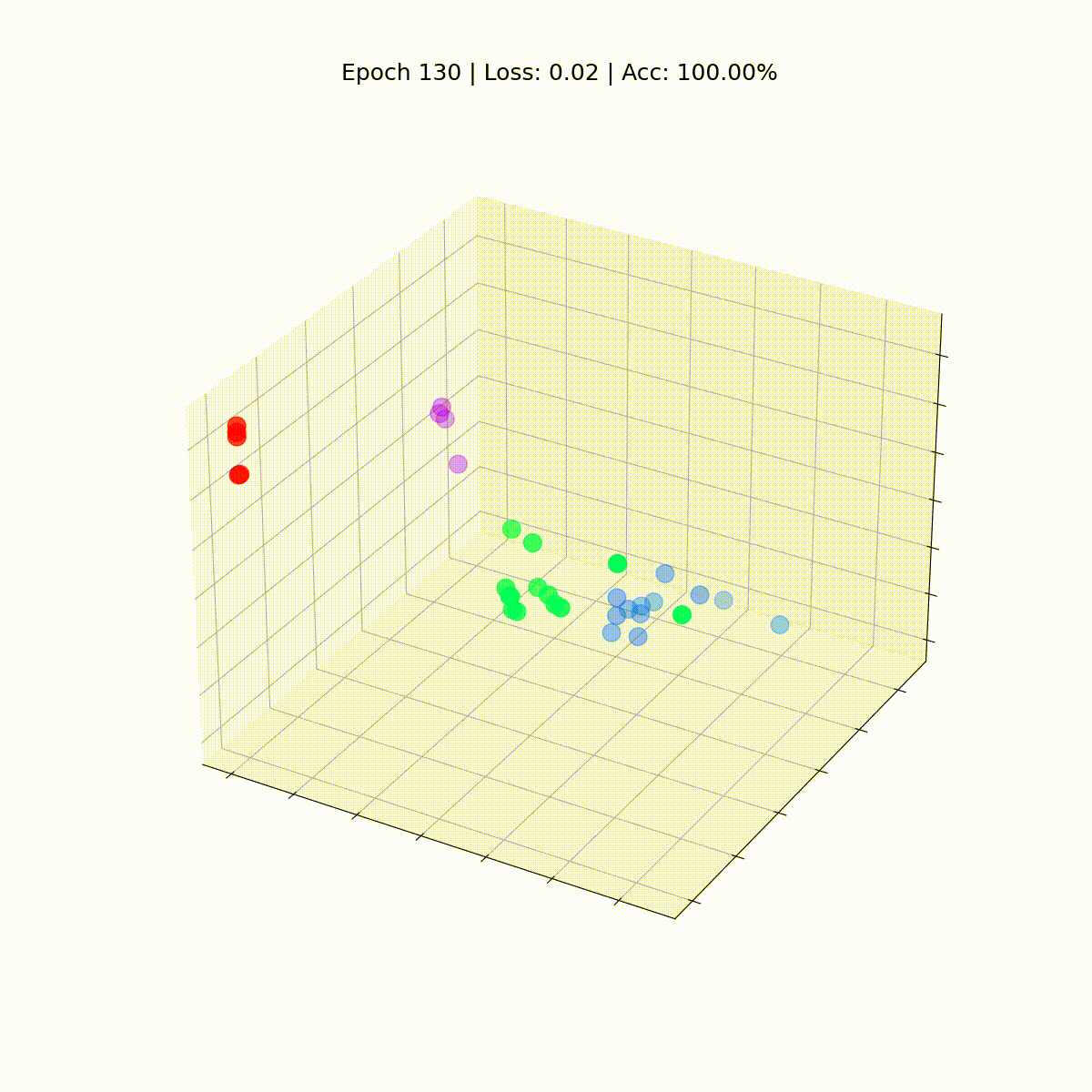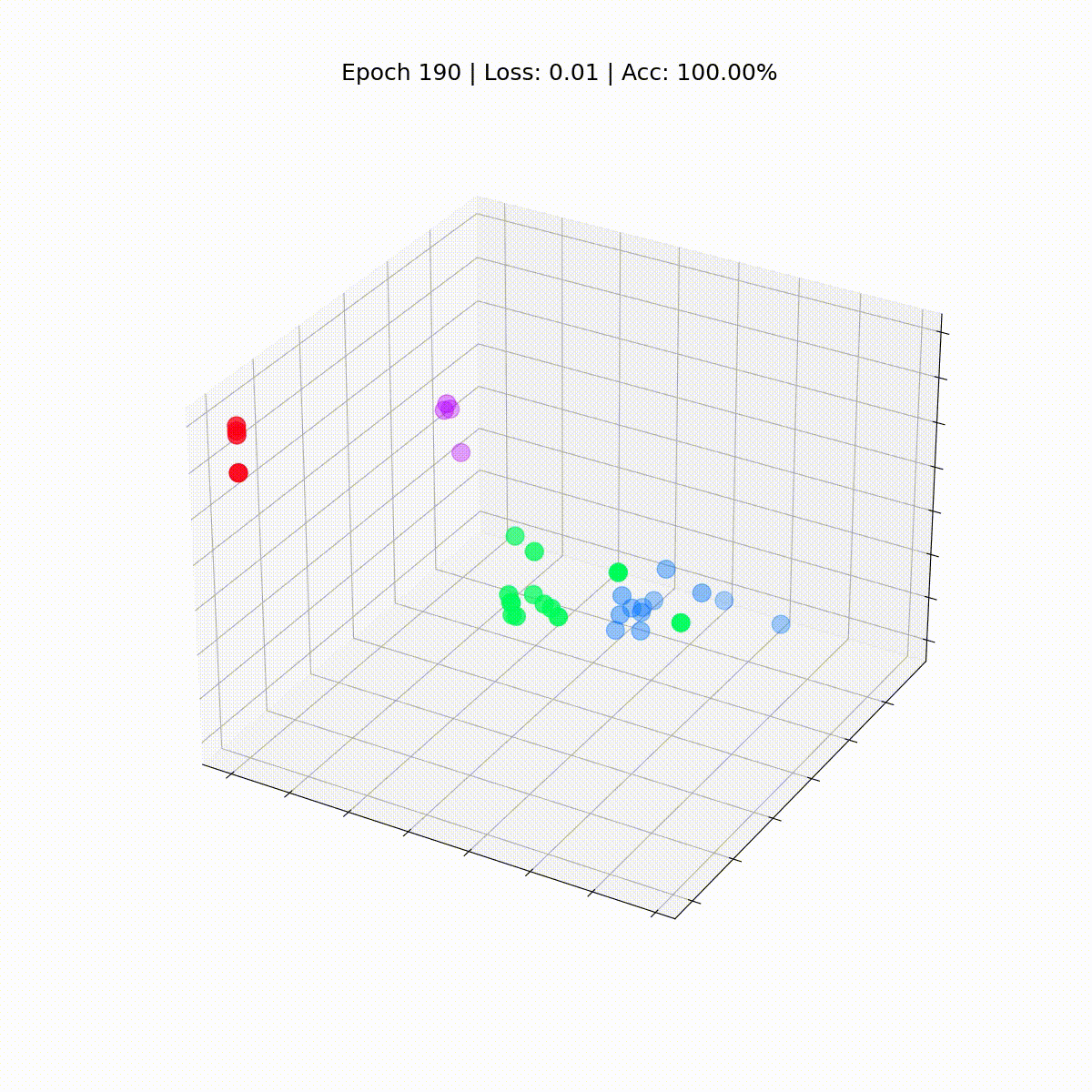
我们的图卷积网络(GCN)已经有效地学习了将相似节点分组到不同集群中的嵌入。这使得最终的线性层可以轻松地将它们区分为单独的类。
嵌入并不是GNN独有的:它们在深度学习中随处可见。它们也不必是3D的:实际上,它们很少是。例如,像BERT这样的语言模型会产生768甚至1024维的嵌入。
其他维度存储有关节点、文本、图像等的更多信息,但它们也会创建更难训练的更大模型。这就是为什么尽可能长时间地保持低维嵌入是有利的。
五、结论
图卷积网络是一种令人难以置信的多功能架构,可以应用于许多上下文。在本文中,我们熟悉了 PyTorch 几何库和对象,如 和 。然后,我们成功地从头开始重建了一个图卷积层。接下来,我们通过实现GCN将理论付诸实践,这使我们能够了解实际方面以及各个组件如何相互作用。最后,我们可视化了训练过程,并清楚地了解了这种网络所涉及的内容。DatasetsData
Zachary的空手道俱乐部是一个简单的数据集,但它足以理解图数据和GNN中最重要的概念。虽然我们在本文中只讨论了节点分类,但GNNs还可以完成其他任务:链接预测(例如,推荐朋友),图分类(例如,标记分子),图生成(例如,创建新分子)等等。
除了GCN之外,研究人员还提出了许多GNN层和架构。在下一篇文章中,我们将介绍图注意力网络(GAT)架构,该架构通过注意力机制动态计算GCN的归一化因子以及每个连接的重要性。
如果您想了解有关图神经网络的更多信息,有书《动手图神经网络》深入了解GNN的世界。
马克西姆·拉博纳





![[GitOps]微服务版本控制:使用ArgoCD 部署Grafana Loki](https://img-blog.csdnimg.cn/f4386c4b7c8f4cc9a1c68b39e268b3bf.png)