python进阶之符号计算概述SymPy

一、概述

1.1SymPy简介

SymPy 是一个由 Python 编写的符号计算库，它的目标是成为一个全功能的计算机代数系统，同时保持代码简洁、易于理解和扩展。它完全由 Python 写成，不依赖于外部库。SymPy 支持符号计算、高精度计算、模式匹配、绘图、解方程、微积分、组合数学、离散数学、几何学、概率与统计、物理学等方面的功能

1.2SymPy具体应用

从 SymPy 的 1.4 版本文档中，可以看出，SymPy 可以支持很多初等数学，高等数学，甚至研究生数学的符号计算。在初等数学和高等数学中，SymPy 可以支持的内容包括但不限于：

基础计算（Basic Operations）；
公式简化（Simplification）；
微积分（Calculus）；
解方程（Solver）；
矩阵（Matrices）；
几何（geometry）；
级数（Series）；

在更多的数学领域中，SymPy 可以支持的内容包括但不限于：

范畴论（Category Theory）；
微分几何（Differential Geometry）；
常微分方程（ODE）；
偏微分方程（PDE）；
傅立叶变换（Fourier Transform）；
集合论（Set Theory）；
逻辑计算（Logic Theory）。

1.3快速入门

sympy.exp(1), sympy.I, sympy.pi, sympy.oo

新建符号

在使用符号之前，先要利用 symbols 函数定义符号，语句是：

# 新建符号 x, y
x, y = symbols('x y')

例子

from sympy import *
x, y, z = symbols('x y z')
y = expand((x + 1)**2) # expand() 是展开函数
y

将字符串转换为 SymPy 表达式

利用 sympify 函数可以将字符串表达式转换为 SymPy 表达式。

注意： sympify 是符号化，与另一个函数 simplify （化简）拼写相近，不要混淆。

str_expr = 'x**2 + 2*x + 1'
expr = sympify(str_expr)
expr

转换为指定精度的数值解

可以使用符号变量的 evalf 方法将其转换为指定精度的数值解，例如：

pi.evalf(3) # pi 保留 3 位有效数字

利用 `lambdify` 函数将 SymPy 表达式转换为 NumPy 可使用的函数

如果进行简单的计算，使用 subs 和 evalf 是可行的，但要获得更高的精度，则需要使用更加有效的方法。例如，要保留小数点后 1000 位，则使用 SymPy 的速度会很慢。这时，您就需要使用 NumPy 库。

lambdify 函数的功能就是可以将 SymPy 表达式转换为 NumPy 可以使用的函数，然后用户可以利用 NumPy 计算获得更高的精度。

import numpy
a = numpy.pi / 3
x = symbols('x')
expr = sin(x)
f = lambdify(x, expr, 'numpy')
f(a)
0.8660254037844386
expr.subs(x, pi/3)

多项式和有理函数化简

下面介绍几个用于多项式或有理函数化简的函数。

`expand` (展开)

将多项式展开，使用 expand 函数。例如：

x_1 = symbols('x_1')
expand((x_1 + 1)**2)

$x_{1}^{2} + 2 x_{1} + 1$

`factor` (因式分解)

用 factor 函数可以对多项式进行因式分解，例如：

factor(x**3 - x**2 + x - 1)

$\left(x - 1\right) \left(x^{2} + 1\right)$

实际上，多项式的展开和因式分解是互逆过程，因此 factor 和 expand 也是相对的。

`collect` (合并同类项)

利用 collect 合并同类项，例如：

expr = x*y + x - 3 + 2*x**2 - z*x**2 + x**3
collect(expr, x)

$x^{3} + x^{2} \left(- z + 2\right) + x \left(x^{2} + 2 x + 2\right) - 3$

`cancel` (有理分式化简)

消去分子分母的公因式使用 cancel 函数，例如：

cancel((x**2 + 2*x + 1)/(x**2 + x))

$\frac{1}{x} \left(x + 1\right)$

`apart` (部分分式展开)

使用 apart 函数可以将分式展开，例如：

expr = (4*x**3 + 21*x**2 + 10*x + 12)/(x**4 + 5*x**3 + 5*x**2 + 4*x)
expr

$\frac{4 x^{3} + 21 x^{2} + 10 x + 12}{x^{4} + 5 x^{3} + 5 x^{2} + 4 x}$

apart(expr)

$\frac{2 x - 1}{x^{2} + x + 1} - \frac{1}{x + 4} + \frac{3}{x}$

数列求和：

from sympy import *
x, a = symbols("x a")
Sum(x ** 2, (x, 1, a)).doit()

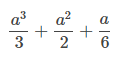
数列求积：

Product(x**2,(x, 1, a)).doit()

输出运算结果的 `latex`代码

使用 latex 函数可以输出运算结果的 latex 代码，例如：

print(latex(integrate(sqrt(x), x)))

\frac{2 x^{\frac{3}{2}}}{3}

二、课堂实操

2.1环境安装和版本检测

import pylab as pl
from sympy import *
import numpy as np
import sympy
sympy.__version__

2.2SymPy 的基础计算

在数学中，基础的计算包括实数和复数的加减乘除，那么就需要在程序中描述出实数与复数。

2.2.1经典公式

著名的欧拉公式 $e^{ix} +1= 0$

from sympy import *
E**(I*pi)+1

公式展开

init_printing(use_unicode=True)#公式显示

#执行SymPy提供的 init printing()可以使用数学符号显示运算结果。
#但它会将Python的内置对象也转换成LateX显示

x = symbols("x")#变量名定义成符号
#x = 2

expand(E**(I*x))#公式展开

2.2.2级数展开

init_printing(use_unicode=True)#公式显示
from sympy import *
x = symbols("x")
tmp = series(exp(I*x),x,0,9)
print(latex(tmp))

$1 + i x - \frac{x^{2}}{2} - \frac{i x^{3}}{6} + \frac{x^{4}}{24} + \frac{i x^{5}}{120} - \frac{x^{6}}{720} - \frac{i x^{7}}{5040} + \frac{x^{8}}{40320} + \mathcal{O}\left(x^{9}\right)$

2.2.3不定积分

$- x \cos{\left (x \right )} + \sin{\left (x \right )}$

tmp=integrate(x*sin(x),x)
tmp
#print(latex(tmp))

2.2.4定积分

tmp=integrate(x*sin(x),(x,0,2*pi))
tmp
#print(latex(tmp))

$\int_{0}^{2 \pi} x \sin{\left (x \right )}\, dx$

Integral(x*sin(x),(x,0,2*pi))

from sympy import *
oo = symbols("oo")
x, y = symbols("x y")
z = integrate(exp(-x**2 - y**2), (x, -oo, oo), (y, -oo, oo))
z.evalf(10)

2.2.5导数

diff(sin(x)*exp(x),x)
#print(latex(diff(sin(x)*exp(x),x)))

$e^{x} \sin{\left (x \right )} + e^{x} \cos{\left (x \right )}$

# 求 3 阶导数
diff(x**4, x, 3)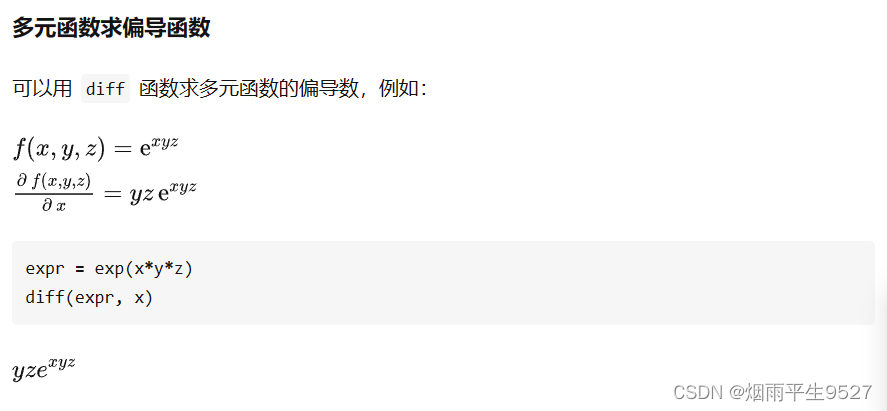

$24 x$

2.2.6微分

t = Derivative(sin(x),x)
t

求解微分方程

使用 dsolve 函数求解微分方程。首先需要建立符号函数变量：

f = symbols('f', cls = Function)
diffeq = Eq(f(x).diff(x, 2) - 2*f(x).diff(x) + f(x), sin(x))
diffeq
dsolve(diffeq, f(x))

Eq 函数是 SymPy 中的一个重要函数，它可以用来创建或判断两个表达式是否相等。Eq 函数的一般用法是：

Eq(左辺, 右辺)

其中，左辺和右辺是两个 SymPy 的表达式，它们可以是符号、数字、函数、多项式等。Eq 函数会返回一个 Eq 对象，它表示左辺和右辺之间的等式关系。

2.2.7极限

limit(sin(x)/x,x,0)

limit(1/x, x, 0, '+')

2.2.8解方程

solve(x**2-4,x)

解线性方程组：

linsolve([x + y + z - 1, x + y + 2*z - 3 ], (x, y, z))

2.2.9表达式变换和公式化简

simplify((x+2)**2-(x-1)**2)

2.2.10矩阵运算

我们在进行矩阵运算之前，需要用 Matrix 构造矩阵，例如：

# 构造矩阵
Matrix([[1, -1], [3, 4], [0, 2]])

$\left[\begin{matrix}1 & -1\\3 & 4\\0 & 2\end{matrix}\right]$

# 构造列向量
Matrix([1, 2, 3])

$\left[\begin{matrix}1\\2\\3\end{matrix}\right]$

# 构造行向量
Matrix([[1], [2], [3]]).T

$\left[\begin{matrix}1 & 2 & 3\end{matrix}\right]$

矩阵转置用矩阵变量的 T 方法。

# 构造单位矩阵
eye(4)

$\left[\begin{matrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{matrix}\right]$

# 构造零矩阵
zeros(4)

$\left[\begin{matrix}0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{matrix}\right]$

# 构造壹矩阵
ones(4)

$\left[\begin{matrix}1 & 1 & 1 & 1\\1 & 1 & 1 & 1\\1 & 1 & 1 & 1\\1 & 1 & 1 & 1\end{matrix}\right]$

# 构造对角矩阵
diag(1, 2, 3, 4)

$\left[\begin{matrix}1 & 0 & 0 & 0\\0 & 2 & 0 & 0\\0 & 0 & 3 & 0\\0 & 0 & 0 & 4\end{matrix}\right]$

矩阵转置

矩阵转置用矩阵变量的 T 方法。例如：

a = Matrix([[1, -1], [3, 4], [0, 2]])
a

$\left[\begin{matrix}1 & -1\\3 & 4\\0 & 2\end{matrix}\right]$

# 求矩阵 a 的转置
a.T

$\left[\begin{matrix}1 & 3 & 0\\-1 & 4 & 2\end{matrix}\right]$

求矩阵的幂

求矩阵 M的 2 次幂：

# 求矩阵 M 的 2 次幂
M = Matrix([[1, 3], [-2, 3]])
M**2

$\left[\begin{matrix}-5 & 12\\-8 & 3\end{matrix}\right]$

特殊地，矩阵的 −1 次幂就是矩阵的逆。

# 求矩阵 M 的逆
M**-1

$\left[\begin{matrix}\frac{1}{3} & - \frac{1}{3}\\\frac{2}{9} & \frac{1}{9}\end{matrix}\right]$

求矩阵的行列式

用矩阵变量的 det 方法可以求其行列式：

M = Matrix([[1, 0, 1], [2, -1, 3], [4, 3, 2]])
M

$\left[\begin{matrix}1 & 0 & 1\\2 & -1 & 3\\4 & 3 & 2\end{matrix}\right]$

M.det()

−1

求矩阵的特征值和特征多项式

用矩阵变量的 eigenvals 和 charpoly 方法求其特征值和特征多项式。

M = Matrix([[3, -2,  4, -2], [5,  3, -3, -2], [5, -2,  2, -2], [5, -2, -3,  3]])
M
M.eigenvals()
{3: 1, -2: 1, 5: 2}
lamda = symbols('lamda')
p = M.charpoly(lamda)
factor(p)

创建了一个 4x4 的矩阵 M，它的元素是：

使用了 M.eigenvals() 方法来求解 M 的特征值，它返回了一个字典，表示 M 的特征值和它们的代数重数。您得到的结果是：

{3:1,−2:1,5:2}

这表示 M 有三个不同的特征值，分别是 3，-2，和 5。其中，3 和 -2 的代数重数都是 1，表示它们各自对应一个线性无关的特征向量；而 5 的代数重数是 2，表示它对应两个线性相关的特征向量。

定义了一个符号变量 lamda，用来表示特征多项式的变量。您使用了 M.charpoly(lamda) 方法来求解 M 的特征多项式，它返回了一个 Poly 对象，表示 M 的特征多项式。您得到的结果是：

λ4−9λ3+18λ2+54λ−225

这表示 M 的特征多项式是一个四次多项式，它的系数是：

[1−91854−225]

使用了 factor 函数来对 M 的特征多项式进行因式分解，它返回了一个表达式，表示 M 的特征多项式的因式分解形式。您得到的结果是：

(λ−3)(λ+2)(λ−5)2

这表示 M 的特征多项式可以分解为三个一次因式和一个二次因式的乘积。这也验证了 M 的特征值和它们的代数重数。

2.2.11数论

阶乘：

factorial(10)

分解质因数：

factorint(300)

factorint(300, visual=True)

求欧拉函数：

totient(25)

判断质数：

isprime(101)
True

求因子：

divisors(36)
[1, 2, 3, 4, 6, 9, 12, 18, 36]