本题是背包问题系列的完全背包问题,和0-1背包唯一的区别就在于:物品是可以重复选取的。 经过之前背包问题的拷打,本题也是一遍AC了。 接下来将给出二维和一维两种做法。
二维dp数组做法:
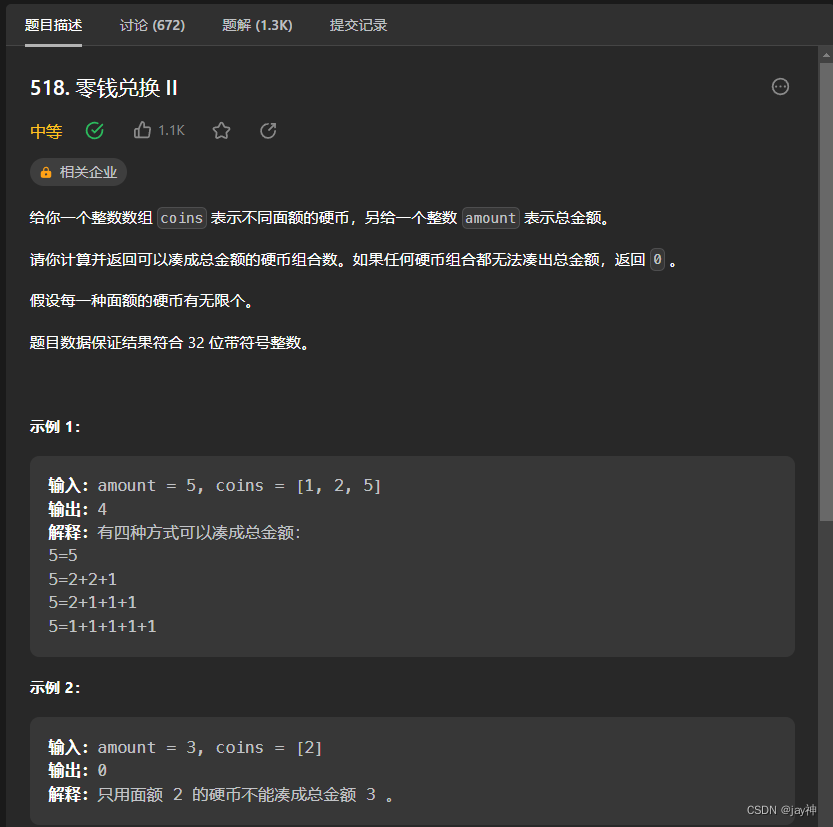
本题的背包大小即为题中给出的总金额:amount。物品即为硬币数组:coins。 需要求出不同硬币组合填满背包的情况种数。 我的解题步骤如下:
- 设定二维dp数组,dp[i][j]的含义为:当背包大小为j时,coins[0]—coins[i]中的元素填满背包的方法个数。
- 初始化二维dp数组的行和列。第一列全初始化为1,因为当背包大小为0时,此时不选取硬币即可填满背包。 第一行需要判断一下:如果用若干个coins[0]可以填满背包,则初始化为1,反之则初始化为0。
- 接下来遍历物品和背包。需要先判断背包能否装下新的硬币。不能装下新硬币:则使用旧dp数组的值,即dp[i][j] = dp[i-1][j]。 能装下新硬币:在不使用新硬币的方法种数基础上,加上使用新硬币的方法种数。 即dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]。 这里有个细节:dp[i][j-coins[i]],这里dp第一个维度使用的是i而不是i-1,因为本题的物品可以重复选取,所以是i。 如果是0-1背包问题,物品不能重复选取,则应该填i-1。
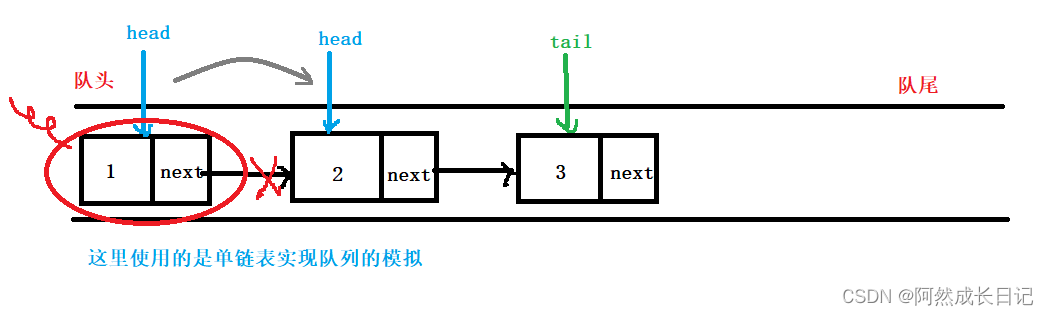
下面给出我画的草稿图以供参考:

代码如下:
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<vector<int>> dp(coins.size(),vector<int>(amount+1));
//初始化dp数组的列
for(int i=0; i<coins.size(); i++)
{
dp[i][0] = 1;
}
//初始化dp数组的行
for(int i=1; i<=amount; i++)
{
//大小为i的背包能用若干个coins[0]的硬币装满
if(i % coins[0] == 0) dp[0][i] = 1;
else dp[0][i] = 0;
}
//遍历硬币
for(int i=1; i<coins.size(); i++)
{
//遍历背包
for(int j=1; j<=amount; j++)
{
//当前背包大小装不下新硬币,即不使用新硬币。
if(j < coins[i]) dp[i][j] = dp[i-1][j];
//使用新硬币和不使用新硬币的总和。 由于硬币可以重复使用,所以是dp[i][j-coins[i]]而不是dp[i-1][j-coins[i]]
else dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]];
}
}
return dp[coins.size()-1][amount];
}
};一维dp数组做法:
代码如下:
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> dp(amount+1 , 0);
dp[0] = 1;
//遍历硬币
for(int i=0; i<coins.size(); i++)
{
//遍历背包
for(int j=coins[i]; j<=amount; j++)
{
dp[j] += dp[j-coins[i]];
}
}
return dp[amount];
}
};ps:遍历背包的时候 j 是从coins[i]开始正序遍历,而之前0-1背包问题是从末尾开始倒序遍历,原因就是本题的物品可以重复选取,所以正序遍历,而0-1背包的物品无法重复选取,所以倒序遍历。