👨‍🎓作者简介：一位即将上大四，正专攻机器学习的保研er
🌌上期文章：机器学习&&深度学习——机器翻译（序列生成策略）
📚订阅专栏：机器学习&&深度学习
希望文章对你们有所帮助

这篇文章实际上应该要接着上次讲过的注意力提示和注意力池化讲的，但是由于学到后面感觉有点不对劲，因为我跳过了一些基础的东西，所以导致transformer的思想有点疑惑，所以暂停了注意力机制的学习，而去实现了机器翻译。
这边接着上次的注意力机制的内容进行学习：
机器学习&&深度学习——注意力提示、注意力池化（核回归）

数学思维推导

注意力分数

在之前使用了高斯核来对查询和键之间的关系建模，而高斯核指数部分可以视为注意力评分函数（简称评分函数），然后把这个函数的输出结果输入到softmax函数中进行运算。通过上述步骤，将得到与键对应的值的概率分布（也就是注意力权重）。最后，注意力池化的输出就是基于这些注意力权重的值的加权和。
下图说明了如何将注意力池化的输出计算称为值的加权和，其中a表示注意力评分函数。由于注意力权重是概率分布，因此加权和其本质上是加权平均值。

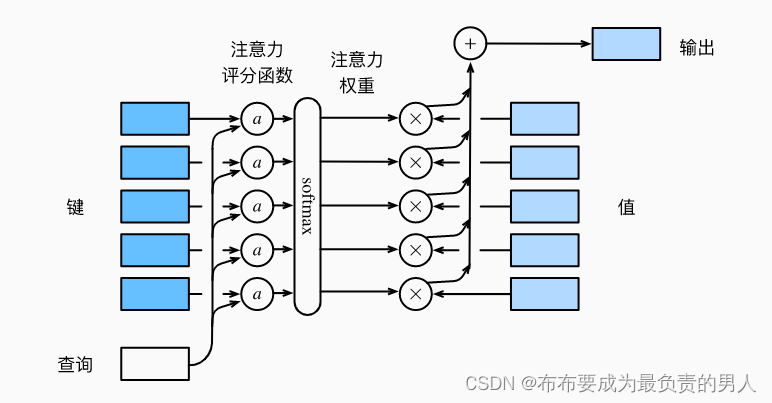
我们可以回顾一下注意力池化的函数f：
$$\begin{gathered} f(x)=\sum _i\alpha (x,x_i)y_i=\sum _{i=1}^{n}softmax(-\frac{1}{2}(x-x_i{)}^2)y_i \\ 其中，\alpha (x,x_i)指的就是注意力权重，而a=-\frac{1}{2}(x-x_i{)}^2指的是注意力分数 \end{gathered}$$

高维拓展

现在让我们拓展到高维度，假设：
$$\begin{gathered} queryq\in R^q，m对key-value(k_1,v_1),...,(k_m,v_m)，这里 \\ {k}_i\in R^k，v_i\in R^v \end{gathered}$$
那么注意力池化层就可以表示为：
$$\begin{gathered} f(q,(k_1,v_1),...,(k_m,v_m))=\sum _{i=1}^m\alpha (q,k_i)v_i\in R^v \\ \alpha (q,k_i)=softmax(a(q,k_i))=\frac{exp(a(q,k_i))}{{\sum }_{j=1}^{m}exp(a(q,k_j))}\in R \end{gathered}$$

注意力分数设计

也就是上面的a函数的设计方式

Additive Attention（key和query不等长时）

Additive Attention也叫做加性注意力
定义三个可学的参数：
$$W_k\in R^{h\times k}，W_q\in R^{h\times q}，v\in R^h$$
此时我们需要和上面一样，把k和q（key和query）结合起来，计算注意力分数：
$$a(k,q)=tanh(W_{k}k+W_{q}q)$$
这时候就很容易看出前面的两个可学参数的意义了，是为了将k和q拉回到同一个维度，方便他们进行计算。
计算出来后的式子一定会是属于R^h的。
那么此时我们计算注意力权重的方式为：
$$\alpha (k,q,v)=v^{T}a(k,q)=v^{T}tanh(W_{k}k+W_{q}q)$$
那么我们最终会得到一个固定的值，这个值就是注意力权重了。
这里的意义我们可以想象得到，这就等价于将key和value合并起来后放到一个隐藏大小为h，输出大小为1的单隐藏层MLP。

Scaled Dot-Product Attention（key和query等长时）

Scaled Dot-Product Attention也叫缩放点积注意力
当query和key都是相同的长度，也就是：
$$q,k_i\in R^d$$
那么可以：
$$a(q,k_i)=<q,k_i>/\sqrt{d}$$
也就是说key和query等长时无须再通过可学习的参数把他们拉回到同一纬度，直接计算点击即可。而除以根号d的用意是为了防止其对于长度过于敏感。
向量化版本：
$$\begin{gathered} Q\in R^{n\times d}，K\in R^{m\times d}，V\in R^{m\times v} \\ 注意力分数：a(Q,K)=Q{K}^T/\sqrt{d}\in R^{n\times m} \\ 注意力池化：f=softmax(a(Q,K))V\in R^{n\times v} \end{gathered}$$

总结

1、注意力分数是query和key的相似度，注意力权重是分数的softmax结果
2、两种常见的分数计算：
（1）将query和key合并起来进入一个单输出单隐藏层的MLP
（2）直接将query和key做内积

实现复杂注意力机制

接下来将用上面的两个流行评分函数来实现更复杂的注意力机制：

import math
import torch
from torch import nn
from d2l import torch as d2l

遮蔽softmax操作

softmax操作用于输出一个概率分布作为注意力权重，但在某些情况下，并非所有的值都应该被纳入到注意力池化中，例如某些文本序列被填充了没有意义的特殊词元等。为了仅将有意义的词元作为值来获取注意力池化，可以指定一个有效序列长度（即词元的个数），以便在计算softmax时过滤掉超出指定范围的位置：

#@save
def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
                              value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)

接下来我们可以验证一下，考虑2个2×4矩阵表示的样本，这两个样本的有效长度分别为2和3，那么超出的部分的softmax值都会被置为0：

print(masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3])))

运行结果：

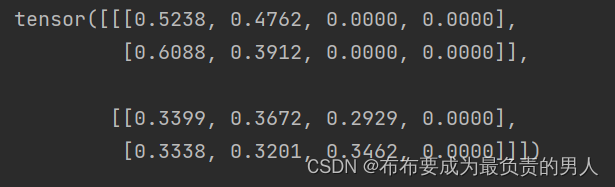
可以看出没啥问题，第一个矩阵都是样本的前两列算，第二个矩阵都是样本的前三列算，当然也满足加起来和为1。
同样也可以使用二维张量，为矩阵样本的每一行都指定有效长度：

print(masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]])))

运行结果：

加性注意力

#@save
class AdditiveAttention(nn.Module):
    """加性注意力"""
    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
        self.w_v = nn.Linear(num_hiddens, 1, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
        queries, keys = self.W_q(queries), self.W_k(keys)
        # 在维度扩展后，
        # queries的形状：(batch_size，查询的个数，1，num_hidden)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # 使用广播方式进行求和
        features = queries.unsqueeze(2) + keys.unsqueeze(1)
        features = torch.tanh(features)
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1)
        self.attention_weights = masked_softmax(scores, valid_lens)
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        return torch.bmm(self.dropout(self.attention_weights), values)

缩放点积注意力

使用点积可以得到计算效率更高的评分函数，但是点积操作要求查询和键具有相同的长度d。下面的缩放点积注意力的实现使用了dropout进行模型正则化。

#@save
class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)

小结

1、将注意力池化的输出计算可以作为值的加权平均，选择不同的注意力评分函数会带来不同的注意力池化操作。
2、当查询和键是不同长度的矢量时，可以使用可加性注意力评分函数。当它们的长度相同时，使用缩放的“点－积”注意力评分函数的计算效率更高。