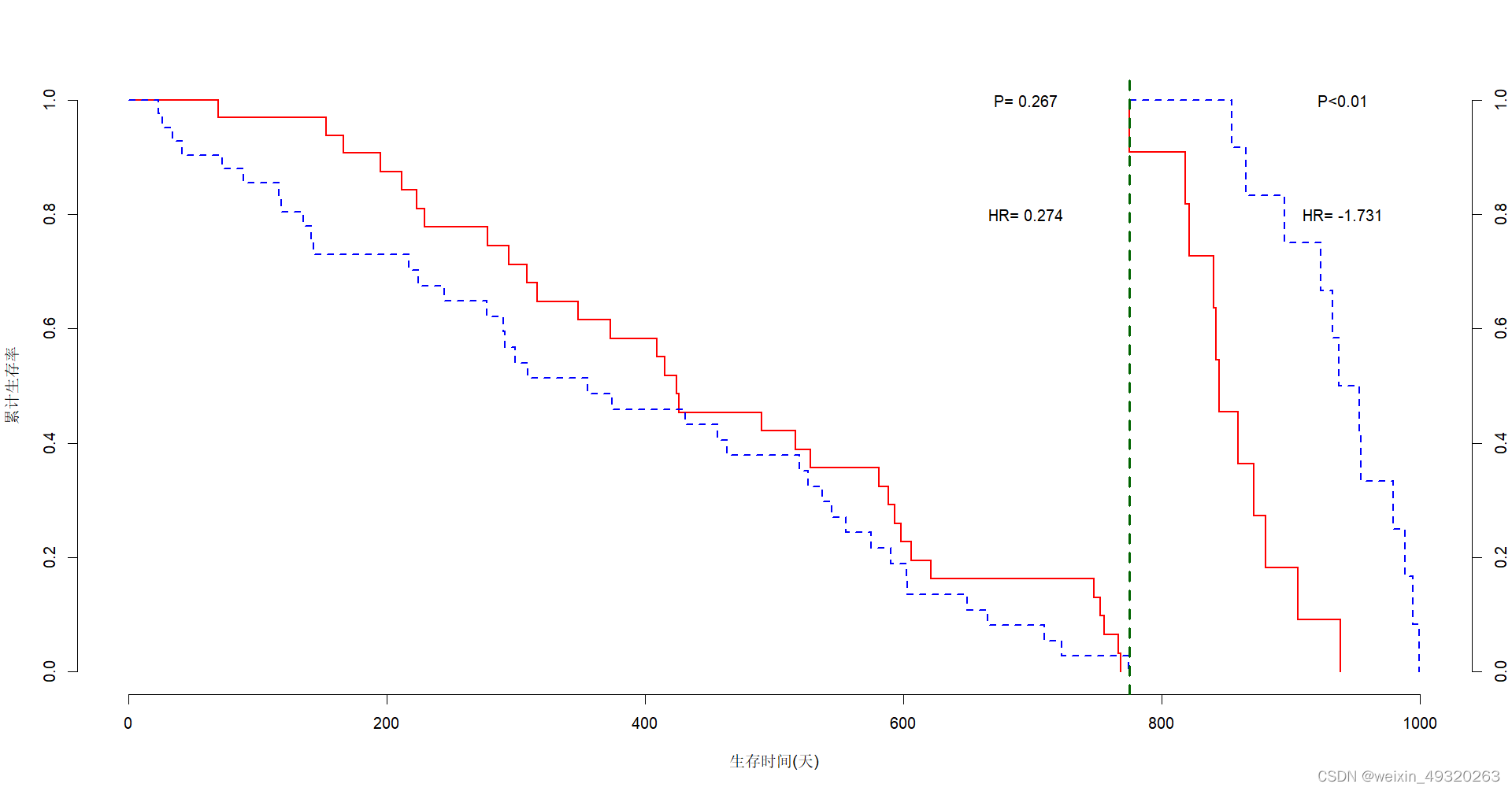
最小生成树(Minimum Spanning Tree,简称 MST)是一个连通图的子图,它包含图中的所有节点,并且是一个树(无环连通图),同时保证连接所有节点的边的权重之和最小。
在一个带权重的连通图中,有许多不同的方式可以连接所有节点,但最小生成树的概念强调的是选择最小权重的边,以使整个树的总权重最小。
有两种常见的算法用于求解最小生成树问题:Prim 算法和 Kruskal 算法。
1、Prim 算法:Prim 算法从一个起始节点开始,逐步地选择连接当前生成树和非树节点的最小权重边,将该节点添加到生成树中,直到所有节点都被包含在生成树中。
2、 Kruskal 算法:Kruskal 算法首先将所有边按照权重从小到大排序,然后从最小权重的边开始逐个加入生成树,但是要保证不形成环路,即所加入的边的两个节点不能在同一个集合中。
ps:Kruskal 算法使用到了 并查集!
1584. 连接所有点的最小费用
给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
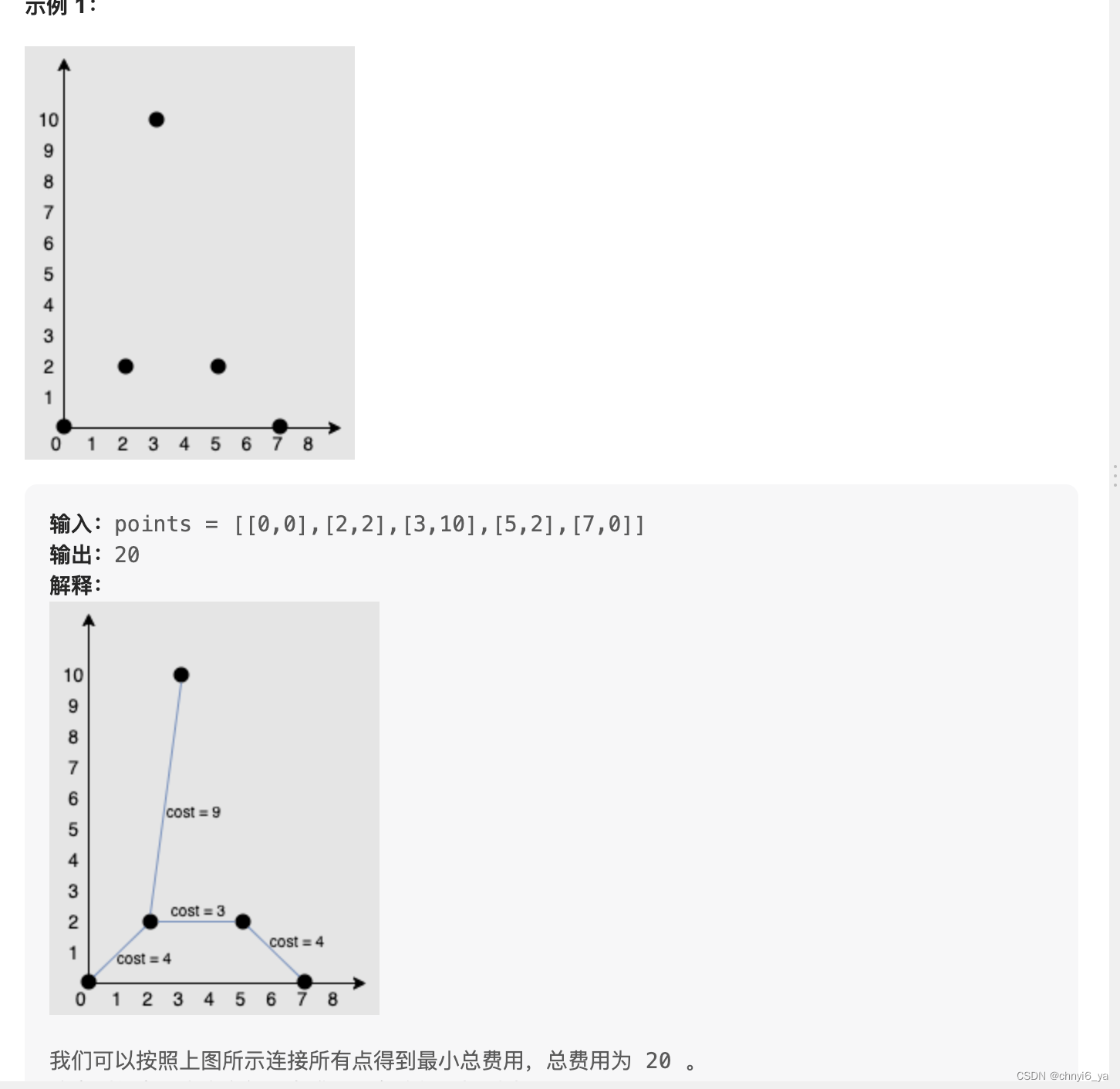
解法
根据题意,我们得到了一张n个节点的完全图,任意两点之间的距离均为它们的曼哈顿距离。现在我们需要在这个图中取得一个子图,恰满足子图的任意两点之间有且仅有一条简单路径,且这个子图的所有边的总权值之和尽可能小。
能够满足任意两点之间有且仅有一条简单路径只有树,且这棵树包含 n 个节点。我们称这棵树为给定的图的生成树,其中总权值最小的生成树,我们称其为最小生成树。
最小生成树有一个非常经典的解法:Kruskal
代码如下:
// 定义了 DisjointSetUnion类,这是一个并查集类,用来管理节点的集合关系
class DisjointSetUnion{
private: // 在 private 下的成员变量和函数只能在 类的内部 访问
vector<int> f,rank;
int n;
public:
// 构造函数
DisjointSetUnion(int _n){
// n个节点
n = _n;
rank.resize(n,1);
f.resize(n);
for(int i = 0;i<n;i++){
f[i] = i;
}
}
// 并查集
int find(int x){
// 路径压缩优化
return f[x]==x? x:f[x]=find(f[x]);
}
// 判断x和y是否在一个集合中,如果已经在一个集合了,返回false
// 如果不在一个集合中,通过rank进行合并
int unionSet(int x,int y){
int fx = find(x), fy = find(y);
if(fx == fy){
return false;
}
if(rank[fx] < rank[fy]){
f[fx] = fy;
}else if(rank[fx]>rank[fy]){
f[fy] = fx;
}else {
f[fx] = fy;
rank[fy]++;
}
return true;
}
};
// 定义结构体Edge
struct Edge{
int len,x,y;
// 是一个构造函数 Edge,用来构造Edge对象
// 通过 len(len), x(x) 和 y(y),将传入的参数分别赋值给结构体的成员变量
Edge(int len,int x,int y):len(len),x(x),y(y){
}
};
class Solution {
public:
int minCostConnectPoints(vector<vector<int>>& points) {
// lambda 函数
// [&] 表示 lambda 函数通过引用捕获外部作用域中的变量,
// 这意味着在 lambda 函数内部, 可以访问外部作用域中的变量。
// 计算x和y这两个点之间的曼哈顿距离
auto dist = [&](int x,int y)-> int {
return abs(points[x][0] - points[y][0])
+ abs(points[x][1] - points[y][1]);
};
int n = points.size();
// 创建了一个名为 dsu 的 DisjointSetUnion 类的对象
DisjointSetUnion dsu(n);
vector<Edge> edges;
for(int i = 0;i<n;i++){
for(int j = i+1;j<n;j++){
// 把每两个点之间的距离、起点、终点放入 vector中
// dist(i, j), i, j 是用于构造 Edge 对象的参数
edges.emplace_back(dist(i,j),i,j);
}
}
// 根据权重来排序Edge,权重越小的排在前面
sort(edges.begin(),edges.end(),[](Edge a,Edge b)->int {return a.len<b.len;});
// num 表示已经连接的点的数量
int ret = 0,num = 1;
//遍历排序后的边,如果两个节点不在同一个集合中,则将它们合并,
// 并将边的长度加入 ret,同时更新 num
for(auto& [len,x,y]:edges){
if(dsu.unionSet(x, y)){
// 合并 x、y
ret += len;
num++;
if(num == n){
break;
}
}
}
return ret;
}
};
1135. 最低成本联通所有城市
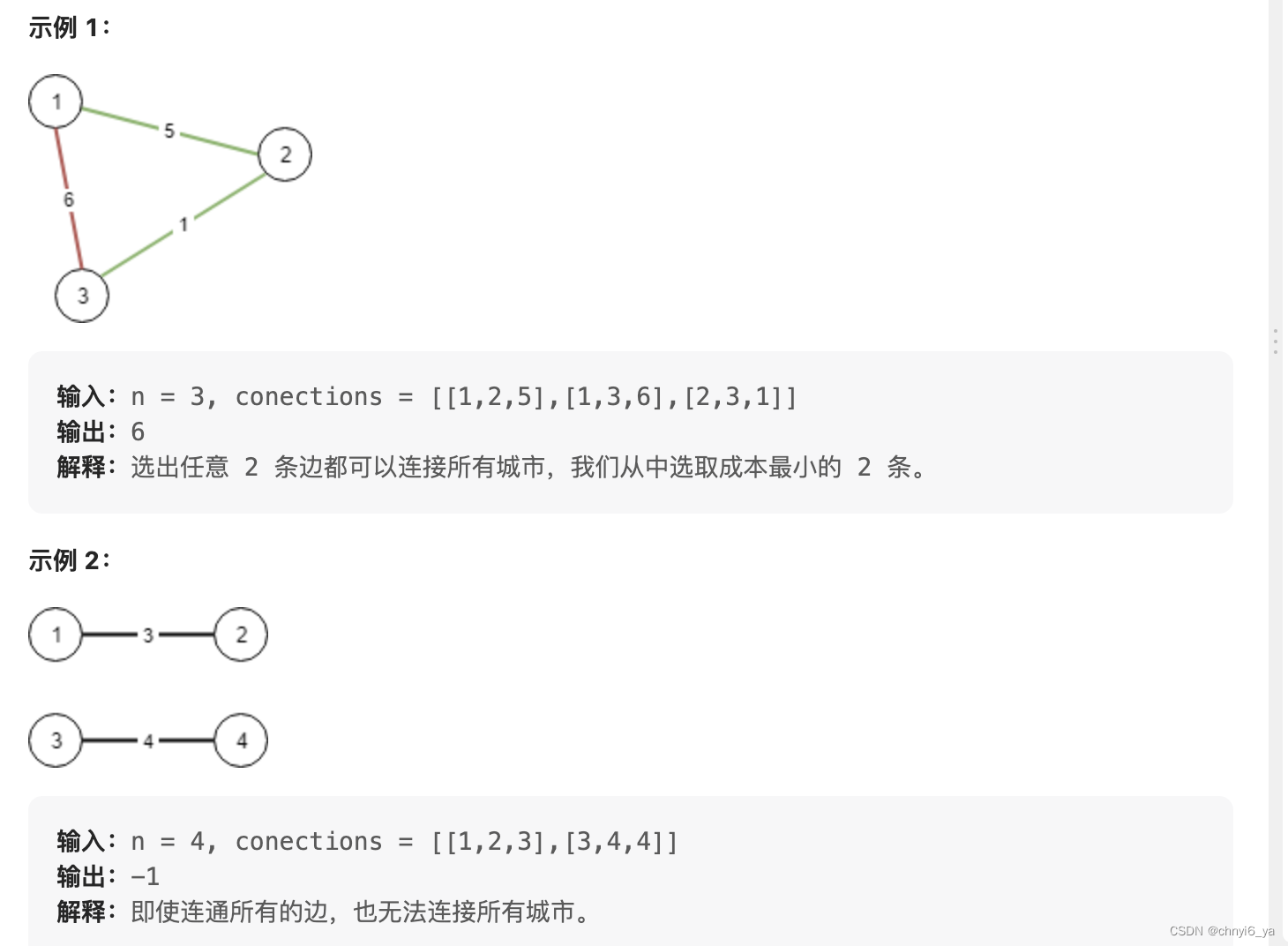
想象一下你是个城市基建规划者,地图上有 n 座城市,它们按以 1 到 n 的次序编号。
给你整数 n 和一个数组 conections,其中 connections[i] = [xi, yi, costi] 表示将城市 xi 和城市 yi 连接所要的costi(连接是双向的)。
返回连接所有城市的最低成本,每对城市之间至少有一条路径。如果无法连接所有 n 个城市,返回 -1
该 最小成本 应该是所用全部连接成本的总和。
代码:
class Solution {
private:
vector<int> father,rank;
public:
// 路径压缩
int Find(int n){
return father[n] == n? father[n] : father[n] = Find(father[n]);
}
// 按秩合并
int unionSet(int x,int y){
int fx = Find(x), fy = Find(y);
if(fx == fy) return false;
if(rank[fx]<rank[fy]){
father[fx] = fy;
}else if(rank[fx]>rank[fy]){
father[fy] = fx;
}else {
father[fx] = fy;
rank[fy]++;
}
return true;
}
int minimumCost(int n, vector<vector<int>>& connections) {
// 初始化father数组
father.resize(n+1,0);
for(int i = 1;i<=n;i++){
father[i] = i;
}
// 初始化rank数组
rank.resize(n+1,1);
// 根据权重重新排一下 connections
sort(connections.begin(),connections.end(),
[](vector<int> a,vector<int> b){
return a[2]<b[2];
});
int ans = 0, num = 1;
for(auto conn:connections){
if(unionSet(conn[0],conn[1])){
// 如果不是一个集合的,进行合并
ans += conn[2];
num++;
}
if(num == n){
break;
}
}
// 如果没有联通所有的点,则返回-1
return num == n? ans:-1;
}
};