1.可视化广度优先搜索和深度优先搜索
此示例说明如何定义这样的函数:该函数通过突出显示图的节点和边来显示 bfsearch
和
dfsearch 的可视化结果。
创建并绘制一个有向图。
s = [1 2 3 3 3 3 4 5 6 7 8 9 9 9 10];
t = [7 6 1 5 6 8 2 4 4 3 7 1 6 8 2];
G = digraph(s,t);
plot(G)
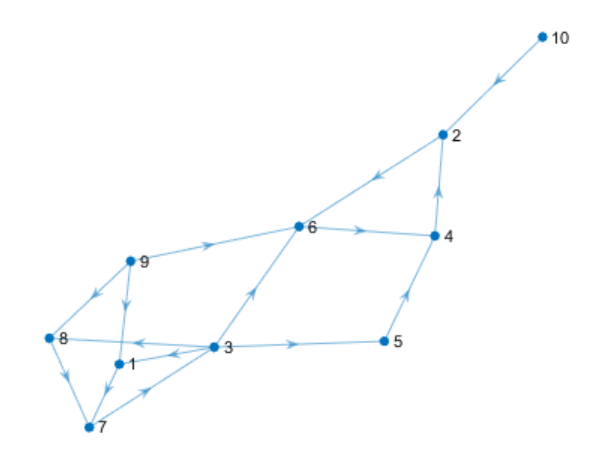
对该图执行深度优先搜索。指定 'allevents'
以便在算法中返回所有事件。此外,将
Restart
指定为
true
以确保搜索会访问图中的每个节点。
T = dfsearch(G, 1,
'allevents'
,
'Restart'
, true)
T =
38x4 table
Event Node Edge EdgeIndex
________________ ____ __________ _________
startnode 1 NaN NaN NaN
discovernode 1 NaN NaN NaN
edgetonew NaN 1 7 1
discovernode 7 NaN NaN NaN
edgetonew NaN 7 3 10
discovernode 3 NaN NaN NaN
edgetodiscovered NaN 3 1 3
edgetonew NaN 3 5 4
discovernode 5 NaN NaN NaN
edgetonew NaN 5 4 8
discovernode 4 NaN NaN NaN
edgetonew NaN 4 2 7
discovernode 2 NaN NaN NaN
edgetonew NaN 2 6 2
discovernode 6 NaN NaN NaN
edgetodiscovered NaN 6 4 9
finishnode 6 NaN NaN NaN
finishnode 2 NaN NaN NaN
finishnode 4 NaN NaN NaN
finishnode 5 NaN NaN NaN
edgetofinished NaN 3 6 5
edgetonew NaN 3 8 6
discovernode 8 NaN NaN NaN
edgetodiscovered NaN 8 7 11
finishnode 8 NaN NaN NaN
finishnode 3 NaN NaN NaN
finishnode 7 NaN NaN NaN
finishnode 1 NaN NaN NaN
startnode 9 NaN NaN NaN
discovernode 9 NaN NaN NaN
edgetofinished NaN 9 1 12
edgetofinished NaN 9 6 13
edgetofinished NaN 9 8 14
finishnode 9 NaN NaN NaN
startnode 10 NaN NaN NaN
discovernode 10 NaN NaN NaN
edgetofinished NaN 10 2 15
finishnode 10 NaN NaN NaN
表 T
中的值对可视化搜索很有用。函数
visualize_search.m
展示了一种方法,使用通过
bfsearch 和dfsearch
执行的搜索的结果,根据事件表
T 突出显示图中的节点和边。该函数在算法中的每一步执行前都会暂停,这样您就可以通过按任意键缓慢地逐步执行搜索。
将 visualize_search.m 保存在当前文件夹中。
function visualize_search(G,t)
% G is a graph or digraph object, and t is a table resulting from a call to
% BFSEARCH or DFSEARCH on that graph.
%
% Example inputs: G = digraph([1 2 3 3 3 3 4 5 6 7 8 9 9 9 10], ...
% [7 6 1 5 6 8 2 4 4 3 7 1 6 8 2]);
% t = dfsearch(G, 1, 'allevents', 'Restart', true);
% Copyright 1984-2019 The MathWorks, Inc.
isundirected = isa(G, 'graph');
if isundirected
% Replace graph with corresponding digraph, because we need separate
% edges for both directions
[src, tgt] = findedge(G);
G = digraph([src; tgt], [tgt; src], [1:numedges(G), 1:numedges(G)]);
end
h = plot(G,'NodeColor',[0.5 0.5 0.5],'EdgeColor',[0.5 0.5 0.5], ...
'EdgeLabelMode', 'auto');
for ii=1:size(t,1)
switch t.Event(ii)
case 'startnode'
highlight(h,t.Node(ii),'MarkerSize',min(h.MarkerSize)*2);
case 'discovernode'
highlight(h,t.Node(ii),'NodeColor','r');
case 'finishnode'
highlight(h,t.Node(ii),'NodeColor','k');
otherwise
if isundirected
a = G.Edges.Weight;
b = t.EdgeIndex(ii);
edgeind = intersect(find(a == b),...
findedge(G,t.Edge(ii,1),t.Edge(ii,2)));
else
edgeind = t.EdgeIndex(ii);
end
switch t.Event(ii)
case 'edgetonew'
highlight(h,'Edges',edgeind,'EdgeColor','b');
case 'edgetodiscovered'
highlight(h,'Edges',edgeind,'EdgeColor',[0.8 0 0.8]);
case 'edgetofinished'
highlight(h,'Edges',edgeind,'EdgeColor',[0 0.8 0]);
end
end
nodeStr = t.Node;
if isnumeric(nodeStr)
nodeStr = num2cell(nodeStr);
nodeStr = cellfun(@num2str, nodeStr, 'UniformOutput', false);
end
edgeStr = t.Edge;
if isnumeric(edgeStr)
edgeStr = num2cell(edgeStr);
edgeStr = cellfun(@num2str, edgeStr, 'UniformOutput', false);
end
if ~isnan(t.Node(ii))
title([char(t{ii, 1}) ' on Node ' nodeStr{ii}]);
else
title([char(t{ii, 1}) ' on Edge (' edgeStr{ii, 1} ', '...
edgeStr{ii, 2},') with edge index ' sprintf('%d ', t{ii, 4})]);
end
disp('Strike any key to continue...')
pause
end
disp('Done.')
close all
使用以下命令对图 G
和搜索结果
T
运行
visualize_search.m
:
visualize_search(G,T)
该图一开始全为灰色,然后每次您按一个键,就会出现一条新的搜索结果。根据以下命令高亮显示搜索结果:
•
'startnode'
- 起始节点的大小变大。
•
'discovernode'
- 节点在被发现后变成红色。
•
'finishnode'
- 节点在完成后变成黑色。
•
'edgetonew'
- 通向未发现的节点的边变成蓝色。
•
'edgetodiscovered'
- 通向已发现的节点的边变成品红色。
•
'edgetofinished'
- 通向已完成的节点的边变成绿色。
2.使用拉普拉斯矩阵为图分区
此示例说明如何使用图的拉普拉斯矩阵来计算 Fiedler 向量。Fiedler 向量可用于将图分区为两个子图。
2.1 加载数据
加载数据集 barbellgraph.mat
,其中包含一个杠铃图的稀疏邻接矩阵和节点坐标。
load
barbellgraph.mat
2.2 绘制图
使用自定义节点坐标 xy
绘制图。
G = graph(A,
'omitselfloops'
);
p = plot(G,
'XData'
,xy(:,1),
'YData'
,xy(:,2),
'Marker'
,
'.'
);
axis
equal
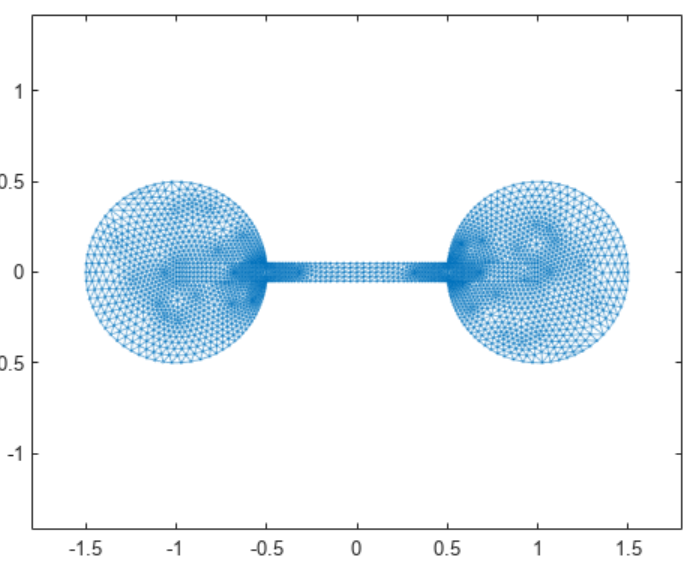
2.3 计算拉普拉斯矩阵和 Fiedler 向量
计算图的拉普拉斯矩阵。然后,使用 eigs
计算两个模最小的特征值和相应的特征向量。
L = laplacian(G);
[V,D] = eigs(L,2,
'smallestabs'
);
Fiedler 向量是对应于该图的次最小特征值的特征向量。最小特征值为零,表示该图包含一个连通分量。这种情况下,
V
中的第二列对应于次最小特征值
D(2,2)
。
D
D = 2×2
10
-3
×
0.0000 0
0 0.2873
w = V(:,2);
由于仅计算特征值和特征向量的子集,因此使用 eigs 求 Fiedler 向量的方法可扩展至更大的图,但对于较小的图而言,将拉普拉斯矩阵转换为满存储并使用
eig(full(L))
同样切实可行。
2.4 为图分区
使用 Fiedler 向量 w 将图分区为两个子图。如果一个节点在 w 中具有正值,则该节点将分配至子图 A。否则,该节点将分配至子图 B。这种做法称为符号切割或零阈值切割。符号切割最大限度减小了切割权重,该权重受限于图的任意非平凡切割的权重上界和下界。使用符号切割对图进行分区。将
w>=0
的节点的子图突出显示为红色,将
w<0 的节点的子图突出显示为黑色。
highlight(p,find(w>=0),
'NodeColor'
,
'r'
)
% subgraph A
highlight(p,find(w<0),
'NodeColor'
,
'k'
)
% subgraph B
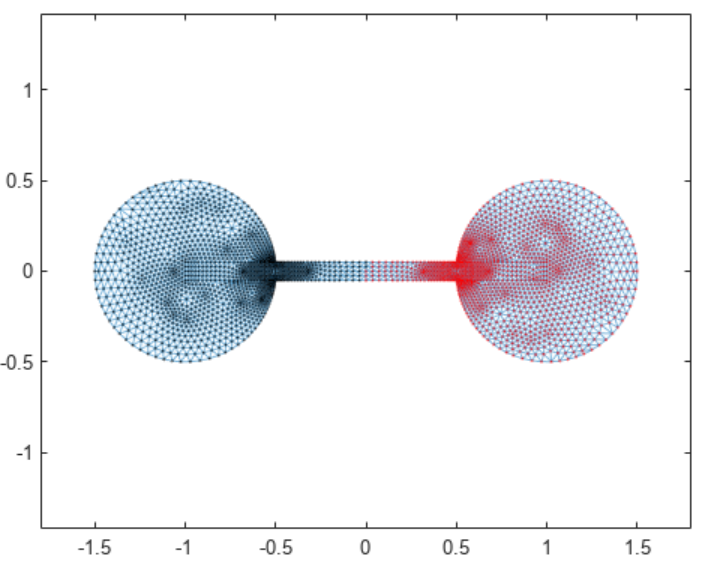
对于该杠铃图而言,此分区恰好将图平分为两个相等的节点集。但符号切割不总是生成平衡切割。任何时候均可通过计算 w 的中位数并将其用作阈值来平分图。这种分区方法被称为中位数切割,它能保证每个子图具有相等的节点数量。使用中位切割时,首先按中位数平移 w 中的值:
w_med = w - median(w);
然后,按 w_med
中的符号对图进行分区。对杠铃图而言,
w 的中位数接近于零,因此两次切割会生成相似的平分。
3.将节点属性添加到图论图数据提示
此示例说明如何自定义 GraphPlot
数据提示以显示图的额外节点属性。
3.1 绘制具有数据提示的 GraphPlot 对象
创建随机有向图的 GraphPlot
图对象。将额外的节点属性
wifi
添加到该图。
rng
default
G = digraph(sprandn(20, 20, 0.05));
G.Nodes.wifi = randi([0 1], 20, 1) == 1;
h = plot(G);
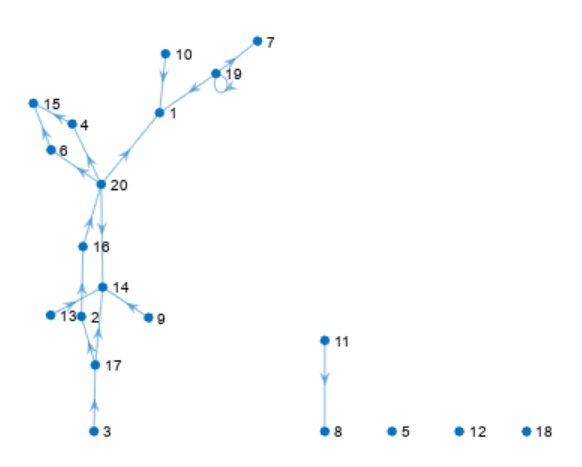
向图中添加数据提示。利用数据提示,您能够选择图论图中的节点并查看节点的属性。
dt = datatip(h,4,3);
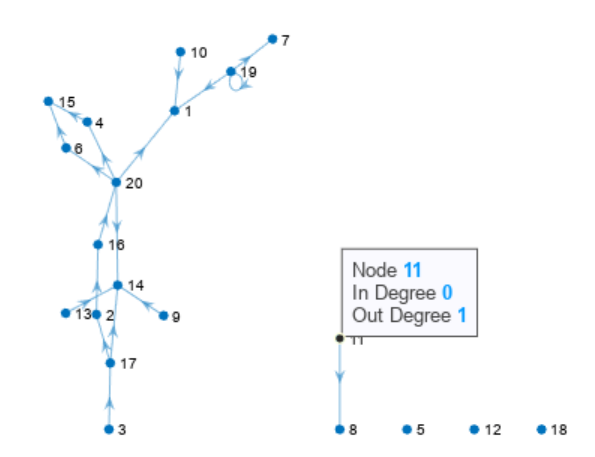
默认情况下,无向图的数据提示会显示节点编号和度。对于有向图,显示内容包括节点编号、入度和出度。
3.2 自定义数据提示中的现有数据
通过在适当的对象属性中添加、编辑或删除数据行,可以自定义图形对象的数据提示显示。对于此GraphPlot
对象:
• GraphPlot
对象句柄是
h
。
• h.DataTipTemplate
属性包含控制数据提示显示的对象。
• h.DataTipTemplate.DataTipRows
属性将数据提示的数据保留为
DataTipTextRow
对象。
• 每个 DataTipTextRow
对象都有
Label
和
Value 属性。您可以通过修改这些属性来调整在数据提示中显示的标签或数据。
更改数据提示中节点行的标签,使其显示为“City”。
h.DataTipTemplate.DataTipRows(1).Label =
"City"
;
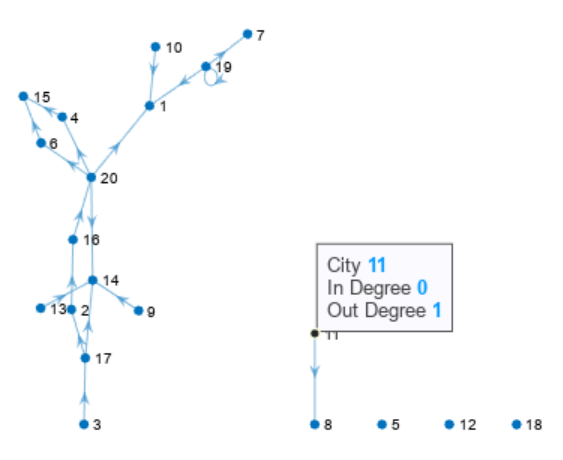
数据提示现在显示城市编号。
3.3 将数据添加到数据提示
dataTipTextRow 函数创建一个可插入
DataTipRows 属性中的新数据行对象。使用 dataTipTextRow 为具有“WiFi”标签的数据提示创建一个新数据行,该数据提示引用图的 G.Nodes.wifi
属性中的值。将此数据提示行作为最后一行添加到
DataTipRows
属性中。
row = dataTipTextRow(
'WiFi'
,G.Nodes.wifi);
h.DataTipTemplate.DataTipRows(end+1) = row;
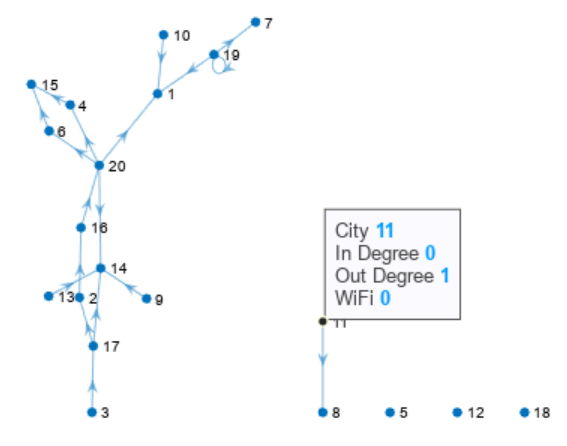
数据提示显示现在包含每个节点的 Wi-Fi® 值。
3.4 从数据提示中删除数据
要从数据提示中删除数据行,可以对 DataTipRows 属性进行索引,并对这些行分配空矩阵 []。这与从矩阵中删除行或列所用的方法可能相同。从数据提示中删除入度和出度行。由于这些行在数据提示显示中显示为第二行和第三行,因此它们对应于DataTipRows
属性的第二行和第三行。
h.DataTipTemplate.DataTipRows(2:3) = [];
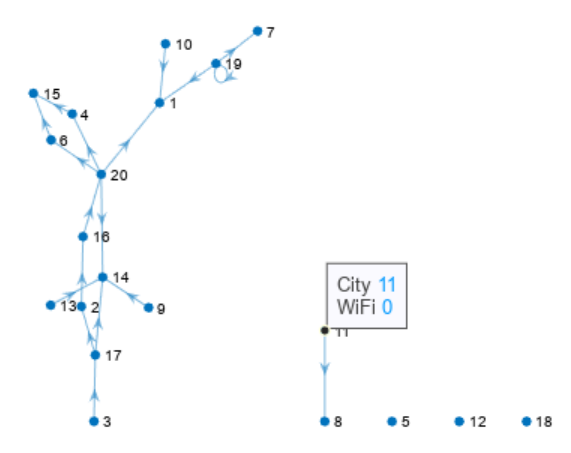
数据提示显示现在只显示城市编号和 Wi-Fi 状态。
4.为图节点和边添加标签
此示例说明如何在图节点和图边上添加和自定义标签。
4.1 创建并绘制图
创建表示某个城市中网格化街道和交叉点的图。为边添加权重,使主干道和横穿街道在图中以不同的方式显示。使用与边权重成比例的边线宽绘图。
s = [1 1 2 2 3 4 4 5 5 6 7 7 8 8 9 10 11];
t = [2 4 3 5 6 5 7 6 8 9 8 10 9 11 12 11 12];
weights = [1 5 1 5 5 1 5 1 5 5 1 5 1 5 5 1 1];
G = graph(s,t,weights);
P = plot(G,
'LineWidth'
,G.Edges.Weight);
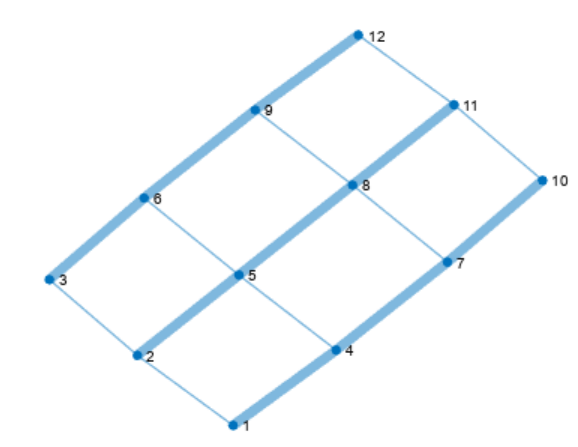
4.2 添加节点标签
对于节点数不超过 100 个的图,MATLAB® 会使用数字节点索引或节点名称自动标记节点(更大的图默认情况下将省略这些标签)。但是,您可以通过调整
GraphPlot
对象
P
的
NodeLabel 属性或使用labelnode 函数来更改节点标签。因此,即使节点具有名称,也可以使用与这些名称不同的标签。删除默认的数字节点标签。将一个交叉点标记为
Home
,将另一个标记为
Work
。
labelnode(P,1:12,
''
)
labelnode(P,5,
'Home'
)
labelnode(P,12,
'Work'
)
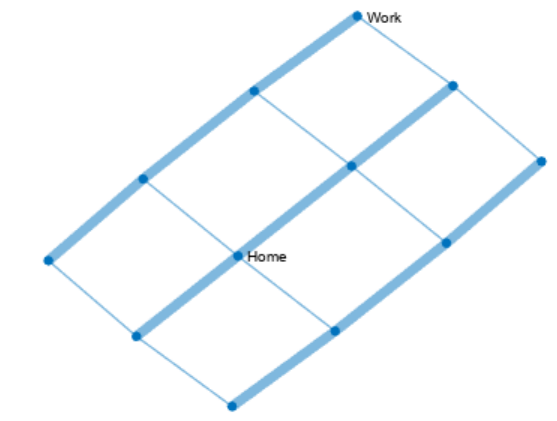
4.3 添加边标签
在绘制的图中,边不是自动标记的。您可以通过更改 GraphPlot
对象
P
的
EdgeLabel 属性值或使用labeledge
函数来添加边标签。
为纽约市的街道添加边标签。边的顺序在图的 G.Edges 表中定义,因此您指定的标签顺序必须遵循该顺序。将边标签直接存储在
G.Edges
表中很方便,这样边名称就位于其他边信息的旁边。
G.Edges
ans=17×2 table
EndNodes Weight
________ ______
1 2 1
1 4 5
2 3 1
2 5 5
3 6 5
4 5 1
4 7 5
5 6 1
5 8 5
6 9 5
7 8 1
7 10 5
8 9 1
8 11 5
9 12 5
10 11 1
⋮
下面的示例有 17 条边,但只有 7 个唯一的街道名称。因此,可以在元胞数组中定义街道名称,然后对元胞数组进行索引,以检索每条边需要的街道名称。将变量添加到包含街道名称的
G.Edges
表中。
streets = {
'8th Ave' '7th Ave' '6th Ave' '5th Ave'
...
'W 20th St' 'W 21st St' 'W 22nd St'
}';
inds = [1 5 1 6 7 2 5 2 6 7 3 5 3 6 7 4 4];
G.Edges.StreetName = streets(inds);
G.Edges
ans=17×3 table
EndNodes Weight StreetName
________ ______ _____________
1 2 1 {'8th Ave' }
1 4 5 {'W 20th St'}
2 3 1 {'8th Ave' }
2 5 5 {'W 21st St'}
3 6 5 {'W 22nd St'}
4 5 1 {'7th Ave' }
4 7 5 {'W 20th St'}
5 6 1 {'7th Ave' }
5 8 5 {'W 21st St'}
6 9 5 {'W 22nd St'}
7 8 1 {'6th Ave' }
7 10 5 {'W 20th St'}
8 9 1 {'6th Ave' }
8 11 5 {'W 21st St'}
9 12 5 {'W 22nd St'}
10 11 1 {'5th Ave' }
⋮
更新 EdgeLabel
属性,以引用这些街道名称。
P.EdgeLabel = G.Edges.StreetName;

4.4 调整字体属性
图论图中的节点标签和边标签具有各自的属性,它们控制着标签的外观和样式。由于属性是分离的,因此可以对节点标签和边标签使用不同的样式。对于
节点
标签,可以调整:
•
NodeLabel
•
NodeLabelColor
•
NodeFontName
•
NodeFontSize
•
NodeFontWeight
•
NodeFontAngle
对于边
标签,可以调整:
•
EdgeLabel
•
EdgeLabelColor
•
EdgeFontName
•
EdgeFontSize
•
EdgeFontWeight
•
EdgeFontAngle
使用这些属性,可以调整此示例中纽约市街道使用的字体:
• 更改 NodeFontSize
和
NodeLabelColor
,使交叉点标签的字体为 12 磅,颜色为红色。
• 更改 EdgeFontWeight
、
EdgeFontAngle
和
EdgeFontSize,为一个方向的街道使用较大的粗体字体,为另一个方向的街道使用较小的斜体字体。
• 更改 EdgeFontName
,使用 Times New Roman 作为边标签。
可以使用 highlight
函数更改图边子集的图属性。创建逻辑索引
isAvenue
,对于包含单词
'Ave' 的边标签,逻辑索引的值为
true
。使用此逻辑向量作为
highlight 的输入,以一种方式标记所有主干道,以另一种方式标记所有非主干道。
P.NodeFontSize = 12;
P.NodeLabelColor =
'r'
;
isAvenue = contains(P.EdgeLabel,
'Ave'
);
highlight(P,
'Edges'
, isAvenue,
'EdgeFontAngle'
,
'italic'
,
'EdgeFontSize'
, 7);
highlight(P,
'Edges'
, ~isAvenue,
'EdgeFontWeight'
,
'bold'
,
'EdgeFontSize'
, 10);
P.EdgeFontName =
'Times New Roman'
;
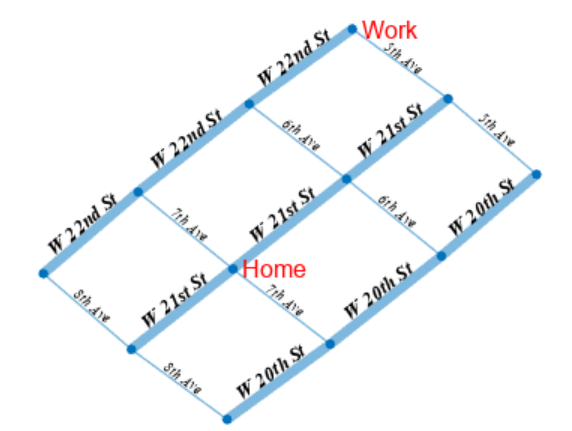
4.5 突出显示边
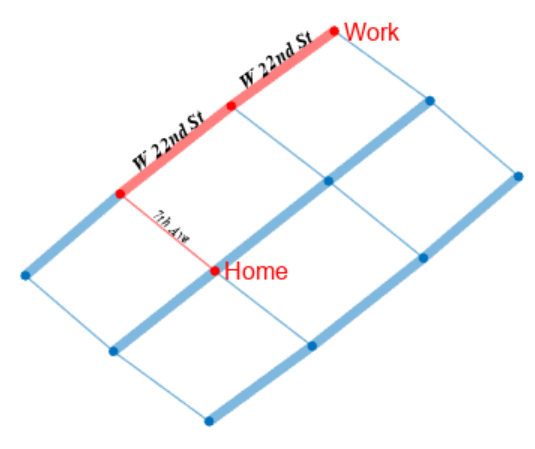
找到 Home 和 Work 节点之间的最短路线,并检查哪些街道在该路线上。以红色突出显示该路线上的节点和边,并删除不在该路线上的所有边的边标签。
[path,d,pathEdges] = shortestpath(G,5,12)
path = 1×4
5 6 9 12
d = 11
pathEdges = 1×3
8 10 15
G.Edges.StreetName(pathEdges,:)
ans = 3x1 cell
{'7th Ave' }
{'W 22nd St'}
{'W 22nd St'}
highlight(P,
'Edges'
,pathEdges,
'EdgeColor'
,
'r'
)
highlight(P,path,
'NodeColor'
,
'r'
)
labeledge(P, setdiff(1:numedges(G), pathEdges),
''
)